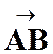1°) COORDONNEES d’un vecteur  DANS UNE BASE ( , )

2°) Coordonnées d’un vecteur  dans un  repère ( O , ,  ) 

a )  Coordonnées d’un vecteur d’origine « O ».

b ) Coordonnées d’un vecteur   ( exemple :  )    défini par un bipoint AB, noté  ( A ; B).

Exercice résolu :

Un plan muni d’un repère , on considère les points   A ( 3 ; 3 ) ; B ( -2 ; 4 ) ; C ( -1 ; -3)

Calculer les coordonnées du vecteur  «  »  et  du vecteur «  »

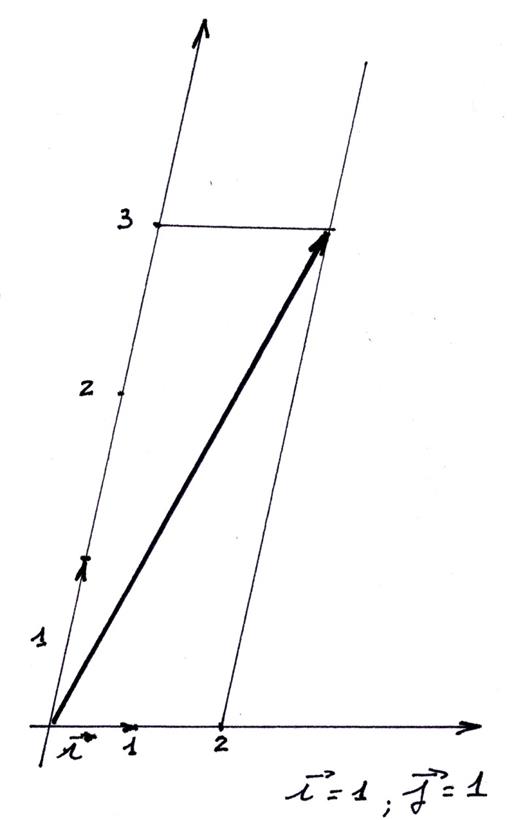
Réponses à trouver  : le vecteur AB :  ( - 4 ; 1 )  et le vecteur  BC : ( 1 ; - 7 )

Procédure  par le tracer : (niveau collège)

Tracer un repère ; le graduer ; repérer les points  ; tracer les projections des points.

Tracer les segments projetés , compter pour chaque segment le nombre de graduations , à ce nombre  associer le signe + ou - (sens de lecture)

Par le calcul : niveau V et plus.(voir ce cours)

COURS :

Rappel sur les CARACTERISTIQUES D ‘UN VECTEUR :

Dans un plan  ( P ) , un vecteur   noté : est défini par :

n sa direction

n son sens

n sa norme

On appelle « repère cartésien » du plan  tout  triplet   ( O ; ,  ) :

                   « O » est un point   ( d ‘ intersection des droites sécantes )

        et      ( , )  est appelé  « base »  ,(formé par le vecteur «  » et le vecteur  «  »)

                   Précision :  le point « I » étant l ‘ extrémité du  vecteur  «  »

                                  et le point  « J » étant l ‘ extrémité du  vecteur  «  »

Représentation graphique

Tout vecteur s'écrit de manière unique comme combinaison linéaire de   et 

1°) COORDONNEES  DANS UNE BASE           ( ,  ) ;  tout vecteur s’écrit d’une manière unique comme combinaison linéaire de et   lorsque  ( ,  )est une base  :   = x+ y

Lorsque   deux vecteurs unitaires  ( ,  )forme  une base:

Pour un vecteur   dans cette base on pourra écrire que  :   = x+ y

a)    x et y sont appelés les coordonnées du vecteur  dans la base ( ,  )  , ou composantes du vecteur                          

Où:

Pour  x :  x  est la première coordonnée du vecteur   ; ( abscisse)

Pour y  :  y est la deuxième coordonnée du vecteur   ; (ordonnée)

L'ensemble dans une base  ( ,  )On dit aussi que : x et y    sont les composantes du vecteur 

non ortho non normé

Exemple :

lorsque l’on donne        = 2+ 3

les coordonnées de     sont  « 2 » et  « 3 »    

 on écrit :         ( 2 ;  3 )  

ou

                     ou         

Il y a donc  3  façons de donner les coordonnées d'un vecteur.

On écrit aussi indifféremment pour donner les coordonnées d'un vecteur:

 (x , y)         ou                  ou                     ;

ces écritures dans une base fixée sont équivalentes à l' écriture :   = x + y

Conseil pédagogique : pour comprendre la suite : voir «  somme de deux vecteurs »  et  « produit d’un vecteur par un nombre »

Résumé 1: somme de deux vecteurs 

         soit deux vecteurs    ( x , y )  et   ( x ’  , y ’ ) alors  + : ( x + x ’ , y + y ’  )

Exemple :  (2 ; -1 )  et    (- 3 ; 4) alors  +: ( (+2 ) + (-3) ;  (-1 ) + ( +4 )  ) ;

                              + : ( - 1 ; +-3) 

Résumé 2 : produit d’un vecteur par un nombre 

                             ( x ;  y)     ;  k.  : ( k x ; k y )

Exemple :    (3 ;  -2 )     ;4  : ( 12 ;  - 8 )

2°) Coordonnées d’un vecteur  dans un  repère  ( O ; ,  ) :

a )  Coordonnées d’un vecteur d’origine « O ».

Les écritures suivantes pour un point A sont équivalentes :

    A ( x ; y ) =   =  x  + y  

Où  « x »  est l’abscisse du point A  et  « y » est l’ordonnée du point  A .

b )Coordonnées d’un vecteur   ( exemple :   )    défini par un bipoint AB, noté  ( A ;B ).

             Soient deux points orientés  A et B : ces points ont pour coordonnées  pour A ( x _A ; y _A) et            pour B ( x _B ; y _B )

     les coordonnées du vecteur       dans le plan sont :

Pour l’abscisse :

l’abscisse de l’extrémité  moins l’abscisse de l’origine : (x _B - x _A ) ;

Commentaire : on recherche le nombre de vecteurs unitaires « » , le sens de déplacement est donné par le signe du résultat .

Si le signe du résultat est « - » le vecteur est orienté de droite vers la gauche ; si le signe est « + » le vecteur est orienté vers la droite. 

Pour  ordonnée :

l’ ordonnée de l’ extrémité moins l’extrémité de l’origine( y _B - y _A)  ;

 Commentaire : on recherche le nombre de vecteurs unitaires « » , le sens de déplacement est donné par le signe du résultat .

Si le signe du résultat est « - » le vecteur est orienté de haut vers la bas ; si le signe est « + » le vecteur est orienté vers le haut. 

EXEMPLE de CALCUL : coordonnées d’un vecteur .

En résumé :          [(x _B - x _A ) ] ; [( y _B - y _A) ]

Application numérique :

Dans un  repère  ( O ; ,  ) :et deux points A ( 1 ; 2 ) et B ( -3 ; 4 ) ( faire la représentation graphique dans un repère cartésien )

 Question :  Déterminer les coordonnées du vecteurs

Sur  « x » ; [( x _B - x _A ) ]    = [ ( -3 ) – ( + 1 ) ]   =  ( - 4 )

Sur « y » ; [( y _B - y _A) ]   = [(+4)  - ( +2 ) ]   = ( +2)

  [(x _B - x _A ) ]  ; [( y _B - y _A) ]  ;

Les écritures suivantes sont équivalentes :

  [( - 4 )  ; ( +2) ]   ;         ( -4 ; 2 )

Commentaire : le vecteur  est orienté de droite à gauche et de bas en haut .

Voir cas :un vecteur et un point A sont donnés ;trouver les coordonnées d’un second point « B » : pour obtenir la translation du vecteur ,

( Intérêt ? conseil pour en savoir plus : égalité de deux vecteurs et « parallélogramme)

Pour avoir la solution , cliquer ici.

ATTENTION : les écritures suivantes ne sont pas équivalentes

A  ( -4 ; 2 )  et    ( -4 ; 2 )

L’écriture

Signifie que  :

A  ( - 4 ; 2 )

Les coordonnées du point A  sont      – 4  sur «  » et    2    sur «»

 ( - 4 ; 2 )

« -  4 » représente un déplacement de 4 vecteurs unitaires «  »sur «  » vers la gauche.

« 2    » » représente un déplacement de 2 vecteurs unitaires «  »sur  l’axe « » vers le haut .

Remarque :  On peut considérer -4  et 2  comme étant les composantes du vecteur AB.

Suite : ( cliquer sur les phrases)

                             3°)  COORDONNEES du milieu de ( A,B)

                              4°)  Conditions pour que des vecteurs soient colinéaires.

Info plus :

                            Conseil : voir « Egalité de deux vecteurs ».

TRAVAUX AUTO FORMATIFS.

CONTROLE:  

1°)Quelles sont les caractéristiques d'un vecteur ?

2°) Combien y a t - i l de façons de donner les coordonnées d'un vecteur dans une base?

3°) citer les 4 façons de données les coordonnées d'un vecteur.

EVALUATION: ..............................................................

Complétez  le graphique et donnez les quatre façons de donner les coordonnées du vecteur « u »   (    )