Pré requis:
ENVIRONNEMENT du
dossier:
|
Objectif suivant |
|
|
|
LES TRANSFORMATIONS GEOMETRIQUES ( généralités)
: |
|
|
|
|
|
|
|
1°)
Déplacement : la translation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
Info Leçon :
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1°) Les
divers « déplacements » : |
|
|
|
|
|
|
|
|
|
·
Rotation |
||
|
|
2°) les oppositions ou symétries, qui, en
géométrie plane , sont des cas particuliers de
déplacements. |
|
|
|
|
|
|
|
|
|
|||
|
|
3°) les divers modes de projections |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
4 °) l’homothétie |
|
|
|
|
|
|
|
|
|
5°) la similitude |
|
|
|
|
Les transformations abordées dans ce document ont
pour propriété commune de transformer une droite en une droite
, mais aussi toute figure « F » en une figure égale
« F’ » |
|
||||||
|
|
|
|
||||||
|
|
Définition : Etant donné un vecteur fixe ( |
|
||||||
|
|
Le vecteur ( |
|
|
|||||
|
|
|
|
||||||
|
|
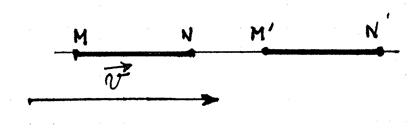
On peut définir la translation d’une autre
manière : c’est le glissement d’une figure « F » ,tel qu’un
segment « MN » qui glisse
sur son propre support pour se placer en « M’N’ » ( par le vecteur : |
|
||||||
|
|
|
|
||||||
|
|
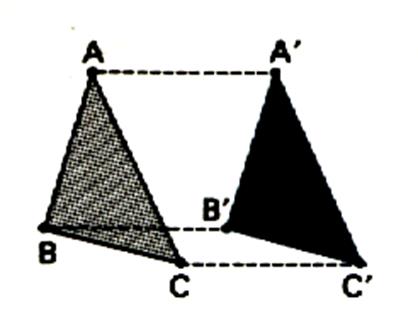
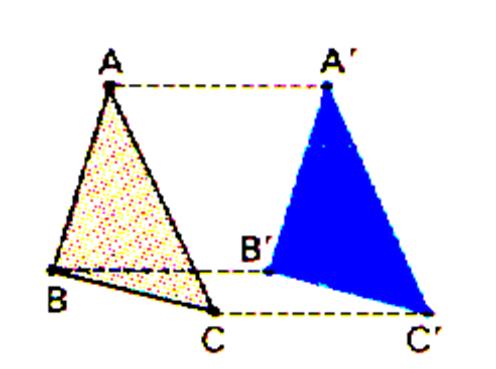
Par exemple : sur la figure ci-contre considérons le point « B ».et le vecteur Pour tout point « B » menons le vecteur
: On obtient le point « B’ » :
« B’ » est dit
« le
transformé de B » dans la translation du vecteur
(
|
|
|
|||||
|
|
La translation est donc un glissement d’une
figure « F », dans lequel :
1°) Tous les points de cette figure décrivent des vecteurs
équipollents. 2°) Toute droite de cette figure reste
parallèle à elle-même , ou bien glisse sur son
propre support. Exemples de translation : le déplacement d’un tiroir
, le déplacement d’un piston dans un cylindre. |
|
||||||
|
|
Réciproquement : |
|
||||||
|
|
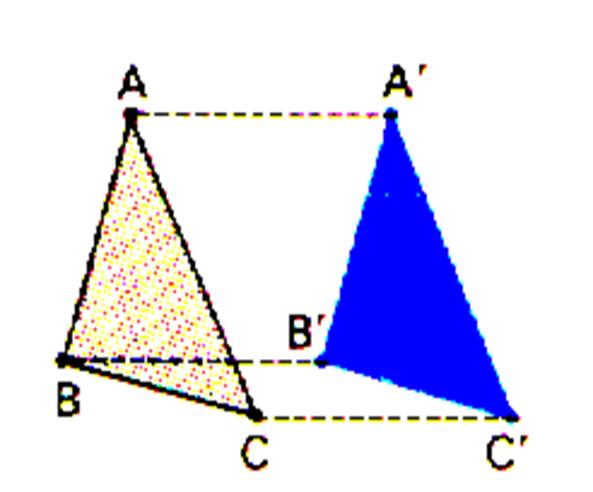
Si deux triangles ABC et A’B’C’ ont pour côtés
homologues
des vecteurs équipollents , une translation pourrait
les faire coïncider , il en sera de même , plus généralement pour deux
figures « F » et
« F’ » se correspondant de telle sorte que tout vecteur de l’une
soit équipollent au vecteur homologue de l’autre . |
|
|
|||||
|
|
|
|
||||||
|
|
Pour en savoir
plus +++sur
la rotation |
|
||||||
|
|
|
|
||||||
|
|
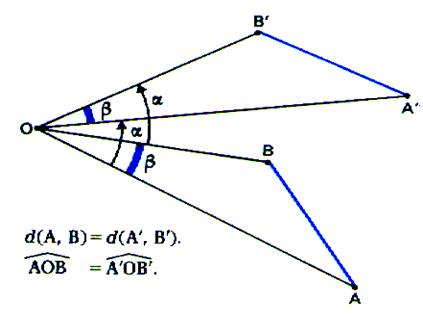
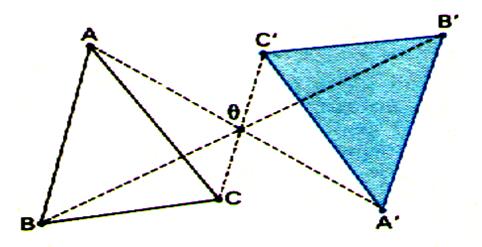
La rotation est un glissement d’une figure , dans lequel : a)
un point
« O » est fixe. b ) Tout point de la figure balaie le même angle « alpha » de
centre « O » |
|
|
|||||
|
|
|
|
||||||
|
|
3°)
SYMETRIE . |
|
||||||
|
|
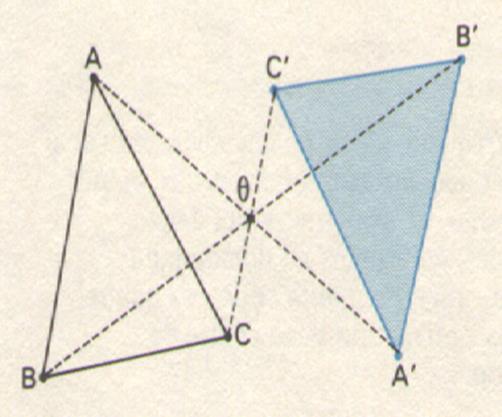
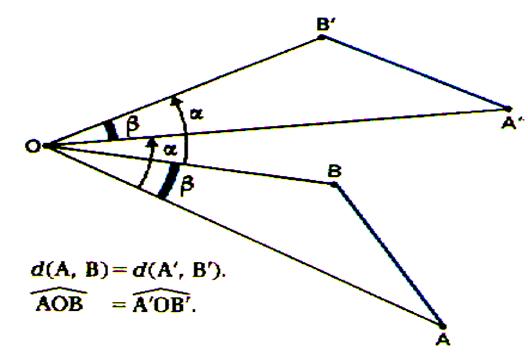
Symétrie par rapport à un point. En géométrie plane , la symétrie par rapport à un point est un cas
particulier de la rotation :c’est une rotation d’un angle plat. Deux figures symétriques par rapport à un point
sont donc superposables par glissement . |
|
|
|||||
|
|
Remarques : La symétrie est aussi un cas particulier de l’homothétie de
rapport –1 |
|
||||||
|
|
Symétrie par rapport à une droite. |
|
||||||
|
|
|
|
|
|||||
|
|
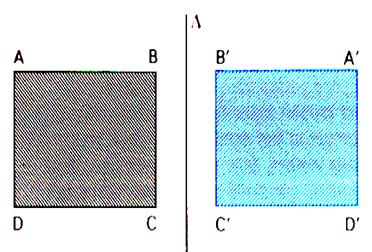
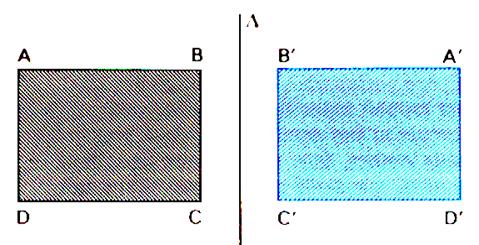
La droite « delta »est l’axe se symétrie . la figure « B’A’D’C’ » est symétrique
de la figure « ABCD » par
rapport à la droite « delta ». |
|
|
|||||
|
|
|
|
||||||
|
|
|
|||||||
|
|
Remarque : |
|
||||||
|
|
|
|
||||||
|
|
Exemple : les deux triangles sont superposables |
|
||||||
|
|
TRAVAUX
AUTO FORMATIFS. |
|
|
|
|
|
|
|
|
|
1°)
Nommer les quatre
transformations géométriques. |
|
|
|
|
|
|
|
|
|
Activités : Identifier les transformations (les
nommer) |
|
|
|
|
|
|
|
|
|
Réponse 1 : |
|
|
|
|
|
|
|
|
|
Réponse 2: |
|
|
|
|
|
|
|
|
|
Réponse 3: |
|
|
|
|
|
|
|
|
|
Réponse 4: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|