Pré requis:

Le quadrillage	ÿü
Les  symétries	ÿü
Le parallélépipède rectangle  ( pavé)	ÿü
Le pavage , carrelage (aire)	ÿü

ENVIRONNEMENT du dossier:

Index  warmaths	Objectif précédent  Les permutations et combinatoires	Objectif suivant :A voir Les pavages périodiques et non périodiques - Fractals	tableau    2°) Les transformations géométriques   3°) Liste des cours sur la symétrie

INFO sur les :  SYMETRIES ET PAVAGES et rotations associées

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité                         les carnets d’Escher   Fiche : carrelage

Corrigé Contrôle

Corrigé évaluation

 

 

 

COURS

 

L’idée de groupe est apparue progressivement tout au long du XIXe  siècle , et le XXe  a montré que c’était l’une des idées les plus importantes de la science contemporaine .

 

Pour expliquer ce dont il s’agit , nous allons utiliser quelques transformations du plan :

 

Les translations    ( ici : INFO plus)

 

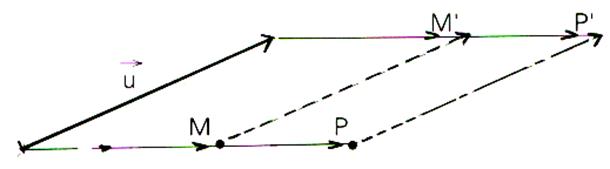
Le Groupe de translation  ( ici : info plus « somme de vecteurs »)

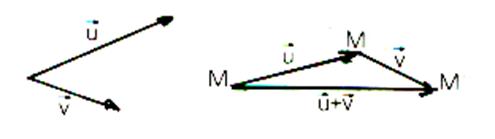
Un autre exemple de groupe est donné par les translations dans le plan , et la composition des translations . La composée de deux translations est encore une translation.

 

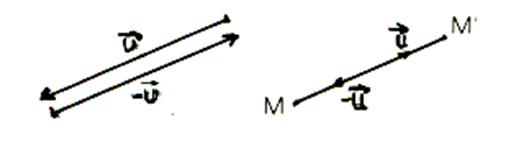
L’identité peut être considérée comme la translation par le vecteur nul , et à chaque translation correspond une translation inverse.

 

 

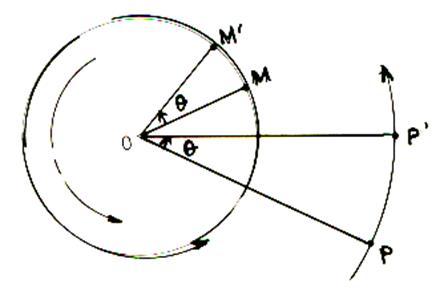
Les rotations	( ici : Info plus ++++sur la rotation )

 

 

 

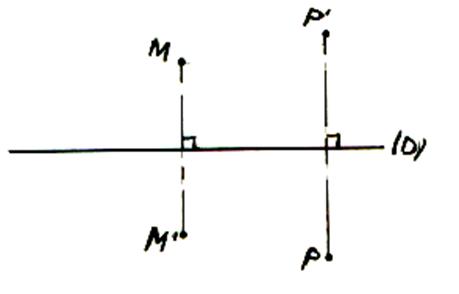
Les symétries axiales	( ici : Info plus +++ sur la symétrie axiale)
Dit aussi : « symétrie orthogonale »

 

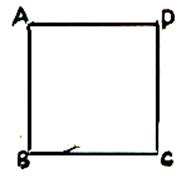
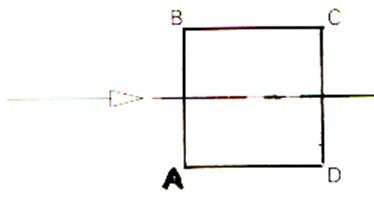
Prenons maintenant un carré

 

( ici : info plus +++ le carré )
Le carré est une figure présentant beaucoup de symétries , de régularité. Pour exprimer cela mathématiquement , on étudie les transformations qui laissent ce carré invariant ; ce sont celles qui transforment le carré en lui-même , certains sommets ayant éventuellement permuté .

 

Etudes de  Cas :

 

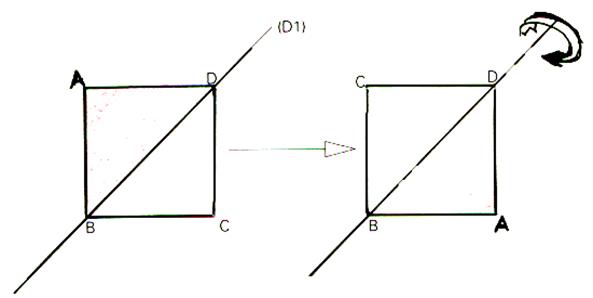
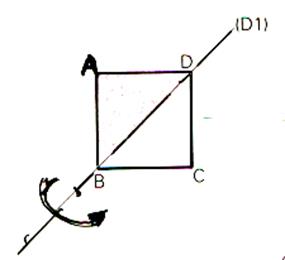
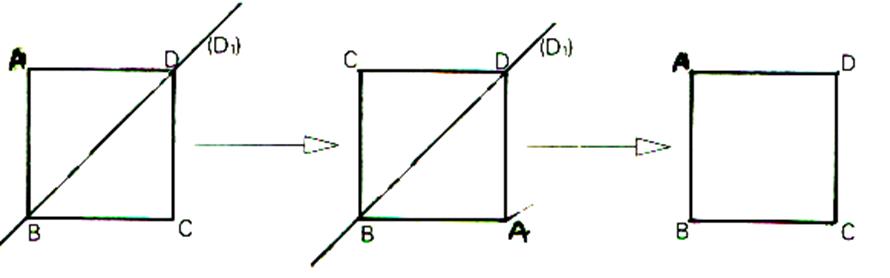
C’est  la cas de la symétrie par rapport à la diagonale ( D1) , qui échange les sommets A et C.

 

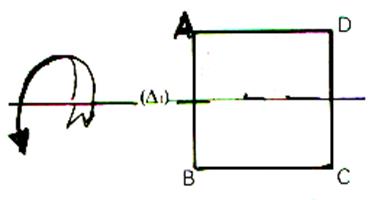
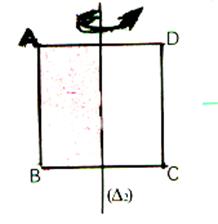
On pourrait tout aussi bien considérer la symétrie par rapport à l’autre diagonale . Mais il y a d’autres symétries laissant ce carré invariant ; celles par rapport aux médiatrices ( D₁)  et ( D₂ )

 

 

 

 

A partir de ces transformations de base , on peut en fabriquer d’autres laissant le carré invariant .Il suffit de les « mettre bout à bout » , de les composer.

 

Par exemple , on peut commencer par faire agir la symétrie d’axe ( D₁) , puis celle d’axe (D₁) , ce qui donne

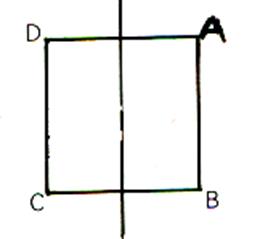
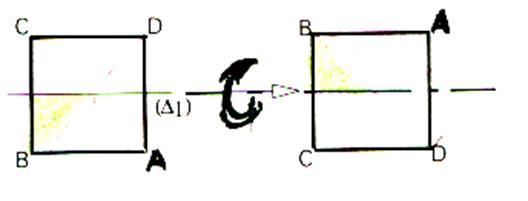
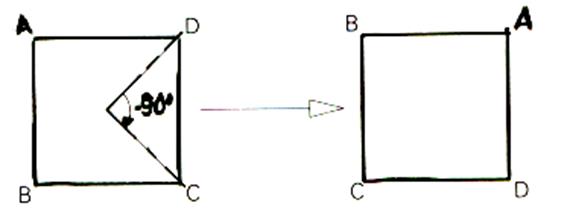
Si nous regardons  ce que sont devenus les sommets par rapport au carré initial :il ont tourné dans le sens des aiguilles d’une montre  d’un quart de tour .

 

  En composant ces deux symétries , nous avons obtenu une nouvelle transformation , qui est en fait la rotation d’angle –90° et de centre le centre du carré.

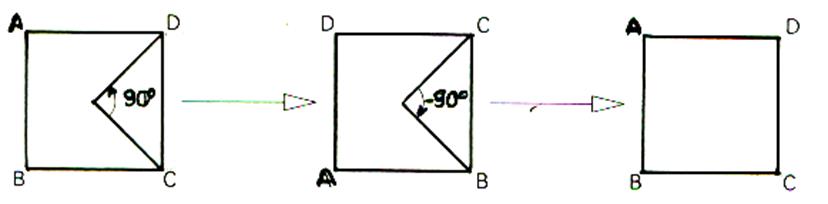
On peut recommencer cela avec n’importe quelles transformations laissant le carré invariant . Ces transformations sont en nombre fini , chacune d’entre elles pouvant être obtenue d’une infinité de manières. Ainsi , si nous prolongeons l’expérience précédente en appliquant de nouveau la symétrie dont l’axe est la diagonale ( D1) .Nous arrivons au même résultat qu’avec  la seule symétrie d’axe ( D ₂) . On démontre qu’il y a exactement huit transformations différentes qui laissent invariant le carré  ( en comptant celle  qui laisse fixe chaque point du plan , appelée « identité »).

 

Remarquer que la transformation inverse ramène les sommets du carré à leur position initiale.

           Par exemple : l’inverse de  la rotation d’angle 90°  est la rotation d’angle –90°  et l’inverse de la symétrie de la symétrie d’axe ( D1) est elle – même .

 

 

	PAVAGE DU PLAN . (abordé en 6e)	( info plus : « art »   et  géométrie  en arithmétique)
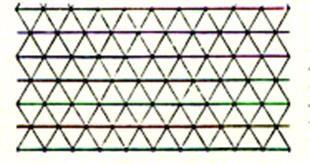
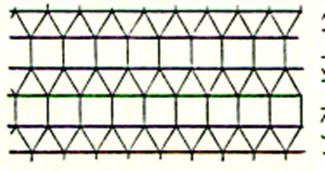
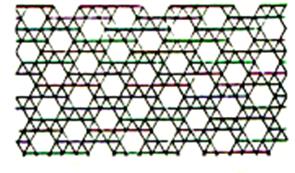
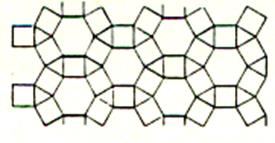
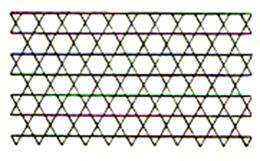
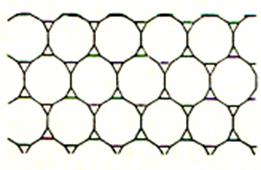
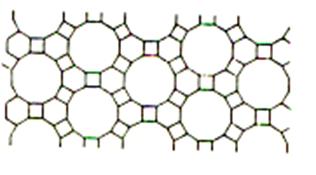
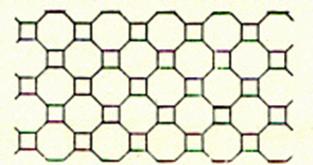
	( mesure des aires : info plus .) Un pavage  du plan est un recouvrement de ce plan obtenu à la manière du carreleur : on prend « des pavés » ou « tuiles » que l’on dispose de façon à ce qu’ils s’emboîtent exactement les uns dans les autres . On décide de n’utiliser qu’un petit nombre de modèles.   Les pavages archimédiens :  ( voir les « nombres archimédiens » ou « nombres arithmétiques »)   Si l’on impose seulement aux pavés d’ être des polygones réguliers placés côté à côté  et tels que les configurations autour de chacun de leurs sommets soient toutes identiques , on obtient onze types de pavages . Ces pavages sont appelés « pavage archimédiens »

 

 

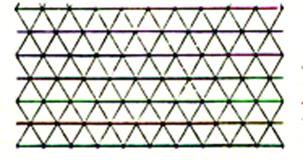
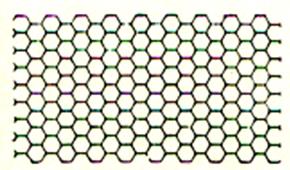
                Il n’y a  que trois pavages du plan dont les pavés sont tous égaux  à un polygone régulier (on impose aux pavés d’être placés côté contre côté) : ceux associés aux triangles équilatéraux , aux carrés et aux hexagones réguliers.

 

Triangles équilatéraux	Carrés	hexagones

 

Commentaire : ce résultat est une conséquence de la formule d’ Euler , présenté dans le livre des permutations .