|
|
|
|
|
|
|
Géométrie : le rectangle |
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif suivant : |
DOSSIER : Classe primaire :
LE PARALLELLEPIPEDE
RECTANGLE ( ou prisme rectangulaire)
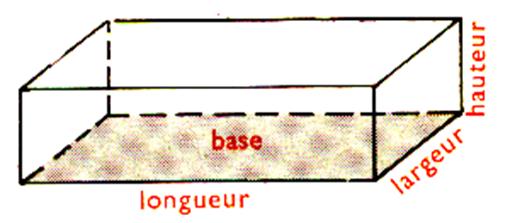
Caractéristiques dimensionnelles de :
· cube ;
· pavé ;
· carreau ;
· panneau ;
· feuille ; ……
|
TEST |
COURS
|
Interdisciplinarité |
|
|||||
|
|
|
Liste des cours
en arithmétique sur les volumes. |
|
|
|
|||
|
|
|
Travaux : niv . VI et V : Dos. : 146 - 147 |
|
|
|
|
||
COURS
TRAVAUX
PRATIQUES
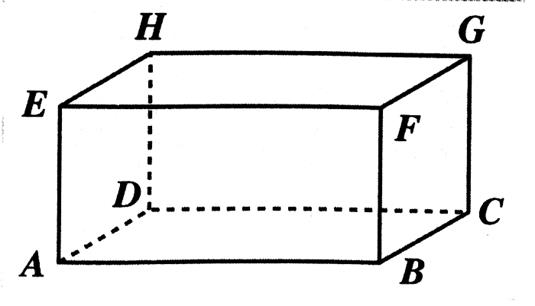
Observons l’emballage d’une lessive :
|
|
|
Le paquet de lessive occupe une certaine place .
C’est un « volume »
Le livre « dictionnaire » peut
être assimilé à un prisme ; c’est un livre « volumineux »
Activité 1 :
LES FACES
|
Questions : |
On doit observer et répondre |
|
Quel est le nombre de ses faces ? |
Le nombre de faces est de 6 |
|
Quelle est la forme de chaque face ? |
rectangulaire |
|
Que pouvons nous
dire des faces opposées ? |
Les faces opposées sont parallèles . |
Par
définition :
un parallélépipède rectangle est un volume qui a 6 faces rectangulaires. Les
faces opposées sont égales .
Les arêtes :
Activités :
1°) A l’aide de 3 feutres ou de 3 craies de couleurs différentes , colorier les arêtes parallèles entres – elles en tentant de les regrouper par couleur.
2°) Quel est le nombre total d’arêtes ? 12
3° ) Mesurer ces arêtes .
4°) Les arêtes d’un même groupes
sont – elles égales ? Sont-elles parallèles ?
5°) A l’aide de l’équerre , mesurer l’angle formé par deux arêtes partant d’un même sommet . Que constatons –
nous ? Que pouvons nous
conclure ?
Identification
des 3 groupes d’arêtes .
|
Les
plus longues |
Les
intermédiaires |
Les
moins longues |
|
|
|
|
Activité 2
Prendre une boîte d’ allumettes
(vide) la recouvrir de papier
blanc
|
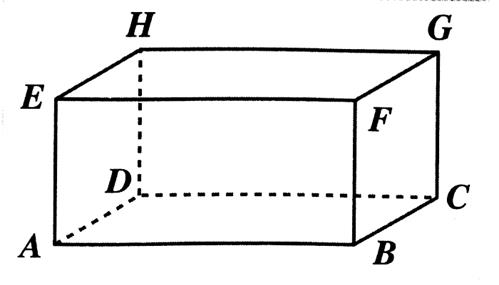
On repère les sommets par une lettre majuscule. Combien y a - t - il de sommets ? Nommer les arêtes : AB ; AE ; AD ; ………. Combien trouve
- t -on d’arêtes ? |
|
Activité 3
|
Prendre la boîte : Mesurer les longueurs des
arêtes et en déduire les 3 dimensions
de chaque face , avec une règle graduée ( mesure au
millimètre prés). |
|
AB = …………..; AE = …………. ; EF = ……. ; FB = …………BC = ……………. CG = …………. ; GF = ………….. ; |
|
Les dimensions se résument à 3
dimensions de longueurs différentes : |
Citer d’autres corps qui , par leur forme ,
ressemblant à ce paquet
Le paquet de lessive a la forme
d’un parallélépipède rectangle.
CONCLUSION :
Le parallélépipède rectangle à 3groupes de 4 arêtes parallèles et égales. Les arêtes d’un groupe sont perpendiculaires aux arêtes
des 2 autres groupes .
Vocabulaire :
Le cube : est un parallélépipède rectangle
dont les longueurs des arêtes sont égales.
Le pavé est un parallélépipède rectangle
dont les dimensions sont proches du cube .
Le « carreau » dit aussi « carrelage » est un parallélépipède
rectangle de faible épaisseur .
Une feuille ou « feuillard » , une
planche , un panneau , un tableau
sont des parallélépipèdes
rectangles de très faible épaisseur .
|
Un
cube |
Un
pavé droit |
Un
carreau |
|
|
|
|
CONTROLE :
Compléter les phrases suivantes (
en vous aidant du cours) :
1°) Le paquet de lessive occupe une certaine place .
C’est un « …………..»
2°)
Par définition : un parallélépipède rectangle est un volume qui a …….. faces ………………. Les faces opposées sont ………… .
3°) Donner la définition d’un parallélépipède rectangle
.
EVALUATION
Fiche :TRAVAUX PRATIQUES
Observons l’emballage d’une lessive :
|
|
|
Activité 1 : LES FACES
|
Questions : |
On doit observer et répondre |
|
Quel est le nombre de ses faces ? |
|
|
Quelle est la forme de chaque face ? |
|
|
Que pouvons nous
dire des faces opposées ? |
|
|
Prendre une boite de la forme d’un parallélépipède rectangle et
mesurer les dimensions de chaque face . |
|
|
Citer d’autres corps qui , par leur forme ,
ressemblant à ce paquet |
|
Le paquet de lessive a la forme
d’un ……………………………………..
Activité 2 : Les
arêtes :
Prendre une boîte d’ allumettes
(vide) la recouvrir de papier
blanc
|
On repère les sommets par une lettre majuscule. Combien y a - t - il de sommets ? Nommer les arêtes : AB ; AE ; AD ; ………. Combien trouve
- t -on d’arêtes ? |
|
Activité 3
|
Prendre la boîte : Mesurer les longueurs des
arêtes et en déduire les 3 dimensions
de chaque face , avec une règle graduée ( mesure au
millimètre prés). |
|
AB = …………..; AE = …………. ; EF = ……. ; FB = …………BC = ……………. CG = …………. ; GF = ………….. ; |
Activité 3 :
1°) A l’aide de 3 feutres ou de 3 craies de couleurs différentes , colorier les arêtes parallèles entres – elles en tentant de les regrouper par couleur.
2°) Quel est le nombre total d’arêtes ? ………….
3° ) Mesurer ces arêtes . :…………………………………..
4°) Les arêtes d’un même groupes
sont – elles égales ? ……………….
Sont-elles
parallèles ? ……………………
5°) A l’aide de l’équerre ,
mesurer l’angle formé par deux arêtes
partant d’un même sommet . Que constatons – nous ?
6° ) Que pouvons nous
conclure ?
Identification
des 3 groupes d’arêtes .
|
1°) On expédie dans une boîte mesurant 45 cm de long
, 23 cm de large et 18 cm de haut , des objets. On
consolide le paquet en collant un ruban adhésif sur toutes les arêtes de la boîte . Quelle est la longueur totale minimale de ruban
que l’on va employer ? |
|
N°2
|
|
Un
laboratoire pharmaceutique ferme les boîtes de médicaments en collant tout
autour un ruban adhésif. Quelle
est la production journalière de boîtes de médicaments si ce laboratoire
utilise quotidiennement 1596 m de ruban adhésif ? |
N°3
|
|
On
veut tapisser une carcasse de bois avec un papier uni. Quel
est la longueur de papier qu’il faudra pour recouvrir les 4 faces ? Un
rouleau mesure 10m de long et 0,60m de
large, combien utilisera-t-on de rouleaux ? |
N° 4
|
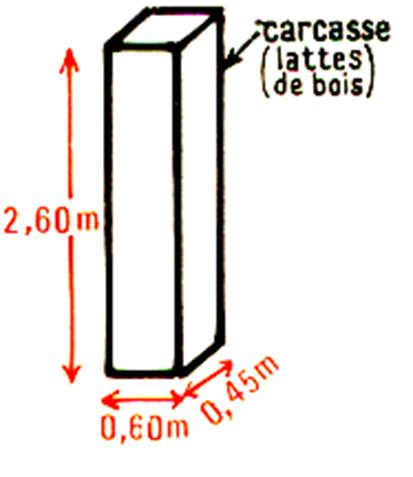
3°)Un coffre à bois sans couvercle a pour dimensions :
1,20 m de long , 0,80m de large et 0,75 m de haut . On
le renforce avec des baguettes d’angles sur les arêtes comme l’indique le croquis
. Quelle
est la longueur de baguette que l’ on doit utiliser
? |
|
N° 5
|
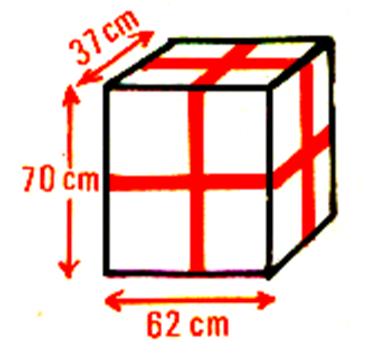
Un grand magasin qui s’installe fait un cadeau - surprise aux 100 premiers clients . Ce cadeau est présenté dans un paquet qui a la
forme d’un parallélépipède rectangle ( cube) . Quelle est la longueur du ruban employé pour
ces 100 paquets
, si l’on compte 25 cm pour le
nœud ? |
|
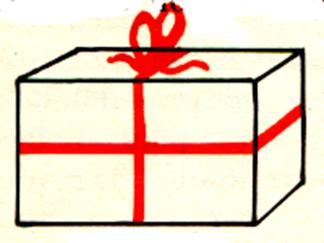
N° 6 Un grand magasin qui
s’installe fait un cadeau - surprise aux
10 000 premiers clients . Ce cadeau est présenté dans
un paquet qui a la forme d’un parallélépipède
rectangle mesurant 25 cm de long , 8 cm de
large et 15 cm de haut . On peut ficeler
le paquet de 3 manières différentes.
Quelle est pour chaque cas ,
la longueur du ruban employé si l’on compte 16 cm pour le nœud ?
|
Cas
1 : |
|
|
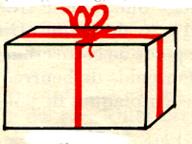
Cas
2 : |
|
|
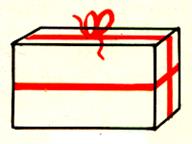
Cas
3 : |
|
La direction du magasin décide d’adopter la solution « 2 ».
Quelle est la longueur totale de ruban nécessaire pour ficeler les 10 000
paquets ?