Les polygones .
|
|
Les parallélogrammes
|
|
ENVIRONNEMENT
du dossier:
|
2°) Les solides de révolution . |
|||||
|
|
|||||
|
|
DOSSIER « géométrie dans l’espace : Le
PRISME . |
|
|||
|
|
|
|
|||
|
|
I ) Définition :
Surface prismatique II )
Définition : « PRISME « III )Définition :
« troncs de prisme » IV ) Le
prisme particulier : le parallélépipède |
|
|||
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
COURS
|
|
|
|
|
|
|
|
PREALABLE : Pour obtenir un prisme il faut deux
surfaces : une surface de base , et une surface prismatique. |
|
|
|
|
|
|
|
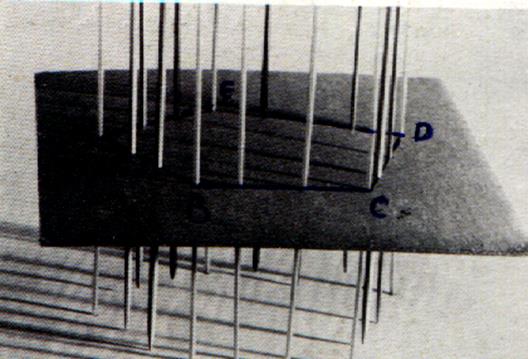
On prend une
plaque de carton rigide , on dessine un polygone (ABCDE). Une tige rigide , piquée en A représente
la droite « delta » (appelée direction) sécante au
plan de la plaque. En piquant d’autres tiges parallèles le long du polygone
(ABCDE) , on engendre une surface appelée
« surface prismatique » |
|
|
|
|
|
|
|
Conclusion : |
|
|
|
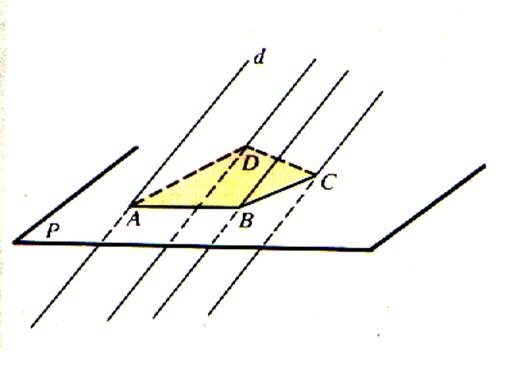
Soit un polygone situé dans un plan P et une droite sécante à P . On appelle « surface
prismatique » , la surface engendrée par les
droites parallèles à d s’appuyant
sur le contour polygonal. Les droites
parallèles à d sont les
génératrices de la surface prismatique. |
|
|
|
Schéma :
|
|
|
|
II ) Définition
« PRISME » : |
|
|
|
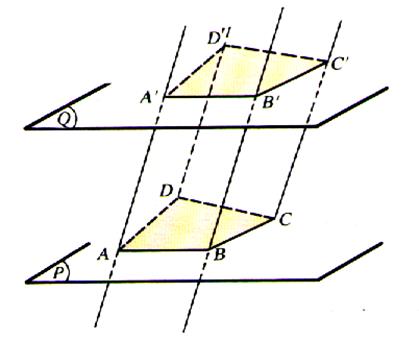
Nous coupons la
surface prismatique de la figure précédente par un plan Q parallèle au plan
P. La section
obtenue est un polygone (A’B’C’D’) ;
(les polygones (A’B’C’D’)et (ABCDE) sont superposables .) |
|
|
|
Définition : Le volume , limité par les faces planes ABCD et A’B’C’D’ et
par la portion de surface prismatique comprise entre les plans P et Q est un
prisme . |
|
|
|
|
|
|
|
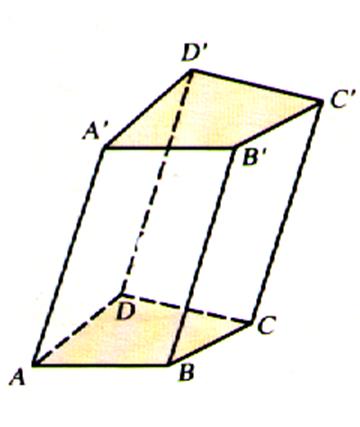
Nous avons donc
le prisme : - les faces ABCD
et A’B’C’D’ sont les bases
du prisme ; -
les faces : AA’B’B ; BB’C’C ; CC’D’D , ;DD’A’A
sont les « faces latérales » . -
les faces : AA’B’B ; BB’C’C ; CC’D’D , ;DD’A’A sont des parallélogrammes. -
Les arêtes latérales [AA’] ;[BB’] ;[CC’] ;[DD’] sont des supports
parallèles et sont de même longueur. |
|
|
|
|
|
|
|
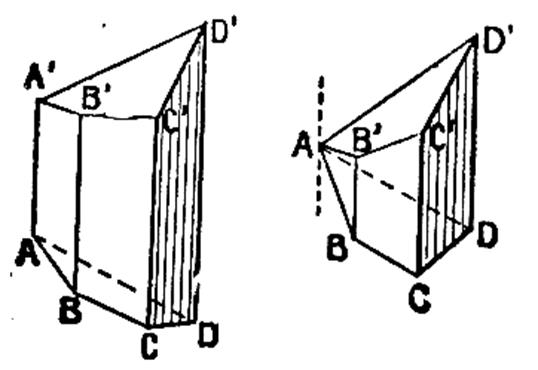
II) TRONCS de PRISME : |
|
|
|
Les
bases ne sont pas parallèles, les arêtes latérales sont parallèles , elles
ne sont donc pas de mêmes longueurs parce que les bases ne sont pas parallèles.. |
|
|
|
|
|
|
|
|
|
|
|
Exemple :
Prisme non droit à base rectangulaire.
|
|
|
|
Exemple :
Prisme droit à base carré.
|
|
|
|
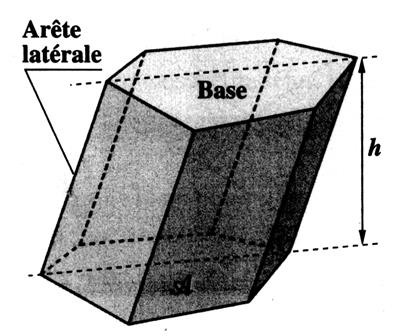
Ci
dessous :
un Prisme oblique à base hexagonale |
|
|
|
|
|
|
|
Ci
dessous :
un Prisme droit à base hexagonale |
|
|
|
|
|
|
|
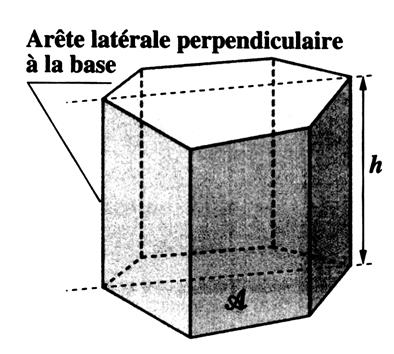
►Un prisme est dit « prisme
droit » si la surface prismatique
est perpendiculaire aux surfaces de base. |
|
|
|
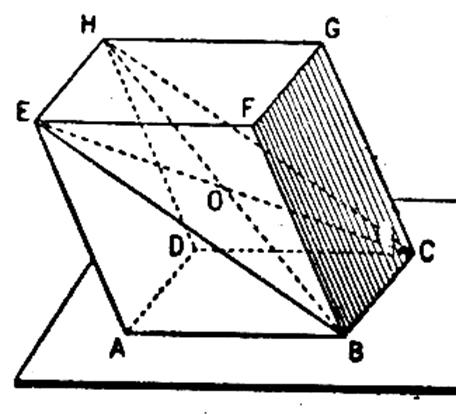
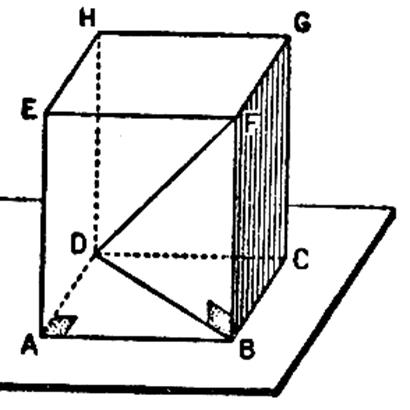
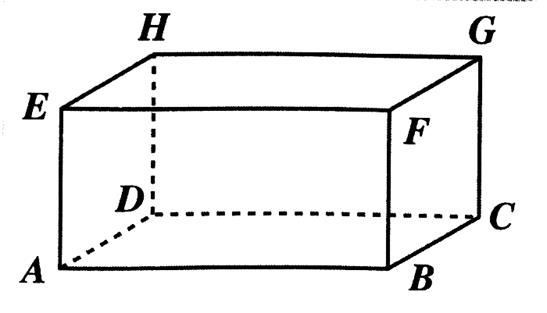
Le
parallélépipède est un prisme droit : Ci dessous , la
base peut être un rectangle ( ADCB ou
EFBA ou un carré ( FGBC) ou
l’une des autres faces paralléles. |
|
|
|
|
|
|
|
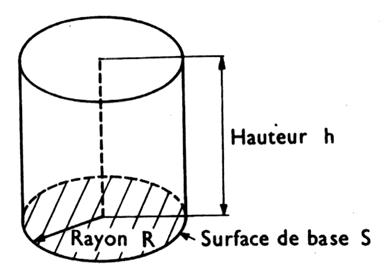
Ci
dessous :
un prisme droit à base circulaire. L’aire latérale est un plan rectangulaire.
( voir le développement d’un cylindre) |
|
|
|
|
|
|
|
IV ) ►Cas particulier
ci dessus :Le parallélépipède : par définition : Un parallélépipède est un prisme
dont la base est un
parallélogramme. Le parallélépipède possède six faces, huit sommets, douze arêtes et
quatre diagonales. Propriétés : -
Les arêtes d’un
parallélépipède sont quatre à quatre
égales et parallèles. -
Les faces opposées d’un parallélépipède sont des
parallélogrammes égaux dont les plans sont parallèles. -
Les quatre diagonales
d’un parallélépipède ont même milieu. Parallélépipède
droit : Un
parallélépipède droit est un parallélépipède dont les arêtes latérales sont
perpendiculaires au plan de base. Parallélépipède
rectangle : Un
parallélépipède rectangle est un parallélogramme droit dont la base est un
rectangle. Ses six faces sont des rectangles. Il est
déterminé par les mesures des trois
arêtes issues d’un sommet. Ces mesures se nomment « dimensions » du
parallélépipède rectangle. Cube : le cube est un
parallélépipède rectangle dont les trois dimensions sont égales. Ses six faces
sont des carrés égaux dont le côté « a » est égal à l’arête du
cube. |
|
|
|
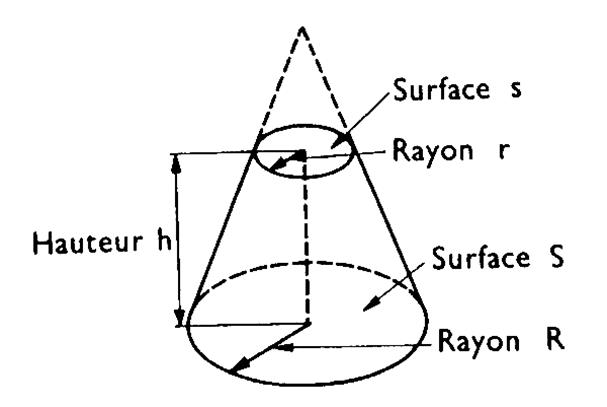
V) ATTENTION les solides ci
dessous ne sont pas des TRONCS
de PRISME |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
|
|
|
|
CONTROLE : 1°) Que faut-il pour obtenir un prisme ? 2°) Donner la définition : Surface prismatique 3°) Donner la définition : « PRISME « 4°) Donner la définition :
« troncs de prisme » 5°) Donner la définition
du prisme particulier : le parallélépipède 6°) Qu’est qu’un
parallélépipède ? EVALUATION
Dessiner un
prisme. |
|
|
|
|
|