Pré requis:
|
|
|
ENVIRONNEMENT du dossier:
Les projections ou
les représentations en perspective linéaires d’un prisme (suite)
|
DOSSIER : « La perspective cavalière » et les Perspectives ,
dites « perspectives linéaires » .
a) La
perspective linéaire cavalière
b) La
perspective linéaire isométrique dite
« axonométrique » :
c) Représentations graphiques des solides, ou de
ses éléments en trois dimensions
)
d) Représentation en perspective d’un prisme ( parallélépipède )
e)
D’autres représentations de solides photographiés.
|
TEST |
COURS |
|
COURS
Définition :
La perspective est une partie de la géométrie qui
enseigne à représenter sur une surface (feuille ;….) les objets avec les
différences de formes , de dimensions et de couleurs dues à leur position .(image)
C’est un procédé de représentation d’une figure sur
un plan au moyen de la projection à partir d’un point « n » en
joignant ce point aux divers points de la figure et en prenant la trace des divers lignes ainsi obtenues sur un plan
( P ) extérieur au point « n ».
Remarques : La perspective permet
de donner une représentation plus claire que celles des vues en projection
orthogonale.
|
Plan du solide ci contre vu en perspective
(dessin technique) |
Remarquer les projections , sur
les « murs perpendiculaires» |
|
|
|
|
Ci dessous sont tracés les vues projetées
sur un plan |
|
|
|
|
Cependant : on peut rarement définir complètement
un ouvrage avec une seule perspective car la cotation est peut
claire.
On choisira toujours la
perspective correspondant le mieux à l’effet souhaité et on limitera au maximum
les arêtes cachées.
|
Rappel : sur la première
loi de la perspective , d’où découle toutes les
autres . |
|
|
Observation :si vous regardez
deux droites parallèles qui s’éloignent , par exemple des rails. |
|
|
a) Si nous devions dessiner ces droites parallèles telles
que nous savons qu’elles sont dans la réalité nous tracerions des parallèles.(voir le plan d’une table en dessin industrie ; nous
traçons un parallélogramme) |
|
|
b) Pour créer l’illusion d’optique de profondeur ;
pour introduire une impression de distance et d’espace dans l’image
plane ; nous traçons des droites dont l’écartement diminue progressivement . ces
droites supposées parallèles converges vers un même
point |
|
D’après la première loi de la perspective : les objets
semble diminuer à mesure que leur distance par rapport à l’observateur s’accroît .
Perspectives utilisées en géométrie
et en sciences
Les deux principales perspectives utilisées en
géométrie pour représenter un solide tridimensionnel sur un plan sont :
a)
la perspective linéaire cavalière :
|
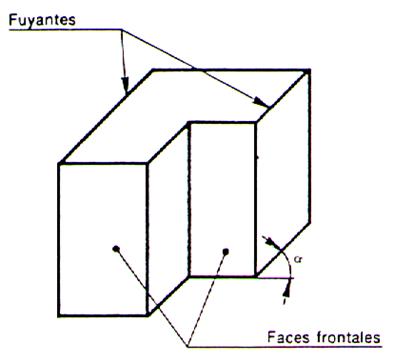
C’est la perspective dont l’exécution est la plus
simple ; elle convient très bien aux dessins rapides ,
mais elle déforme sensiblement l’objet représenté. Principe : Toutes les faces frontales sont dessinées en
vraie grandeur. Toutes les arêtes non frontales se dessinent
suivant des fuyantes inclinées d’un même angle µ et sont réduites dans un rapport
appelé : |
|
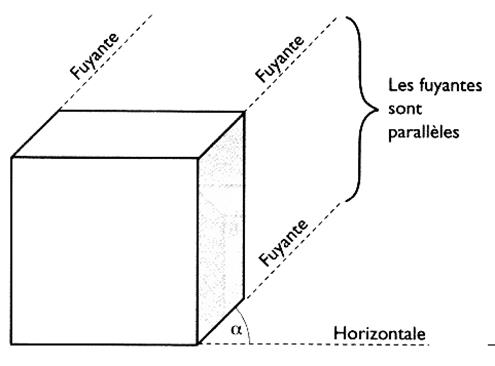
La perspective cavalière d'une figure est caractérisée
par l'angle µ ( alpha) et le coefficient "k" .
- Le parallélisme
est conservé : les arêtes parallèles
sont représentées par des
segments parallèles .
-
les fuyantes , ou lignes
de fuite , parallèles entre elles font un angle µ avec l'horizontale .
Par exemple : sur les fuyantes , avec
k = 0,6 , une arête de longueur 5 cm est représentée par un segment de longueur
: 3 cm ( 5 cm fois 0,6 )
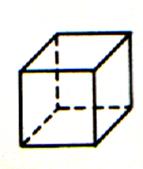
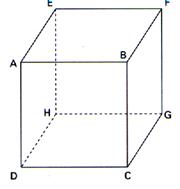
Exemple: perspective d'un cube
activité : dessiner un cube d'arête 5 cm en perspective
cavalière avec l'angle µ = 30° et k = 0,4.
b)
la perspective linéaire isométrique dite
« axonométrique »
:
|
Perspective isométrique . |
|
|
C’est la perspective
axonométrique dont l’exécution est la plus commode ( toutes
les fuyantes sont inclinées de 30° par rapport à l’horizontale ) . Elle s’utilise
couramment pour les schémas de canalisation. |
|
c)
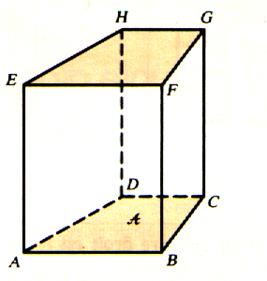
Exemples de solides vus en
perspective
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
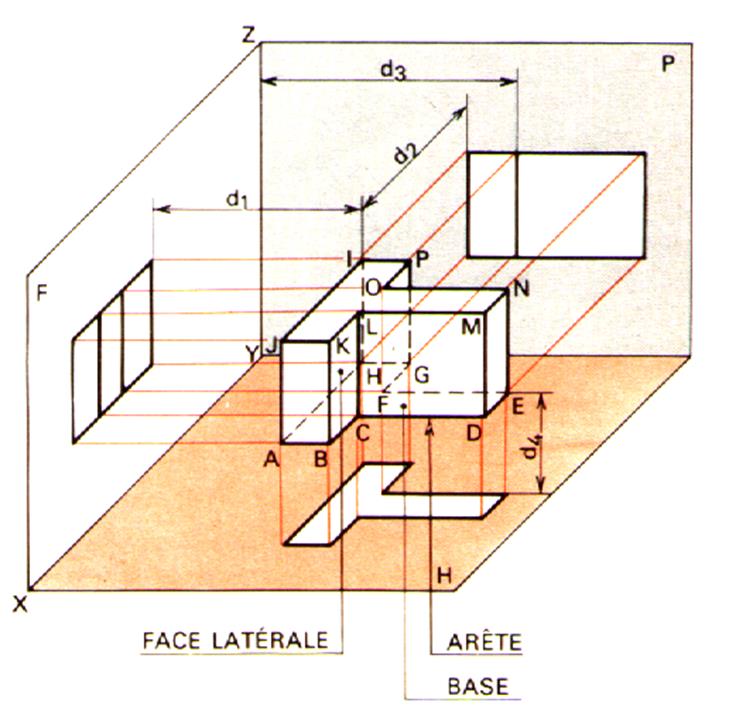
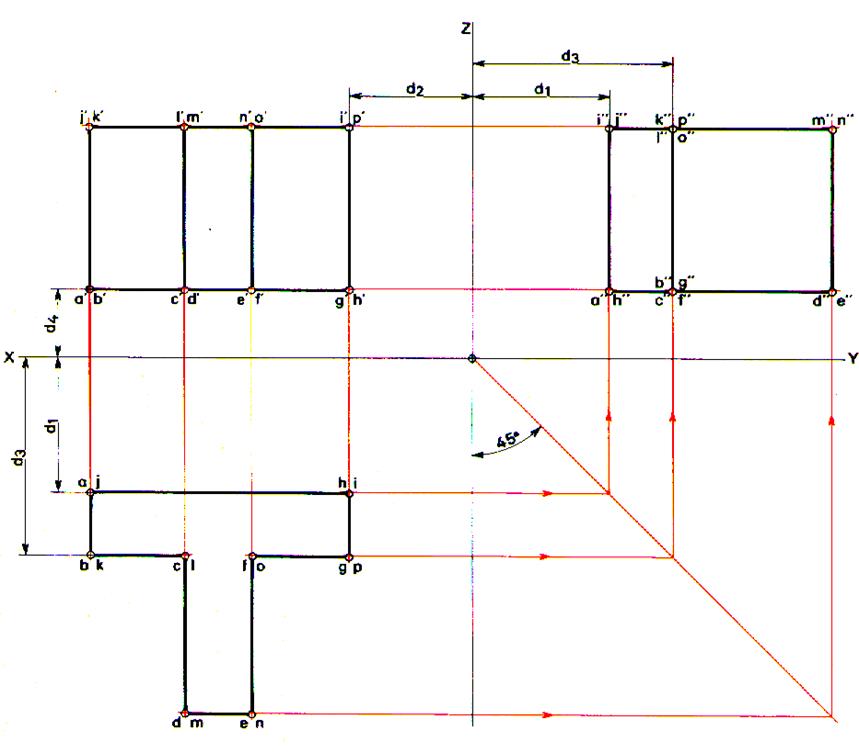
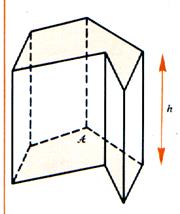
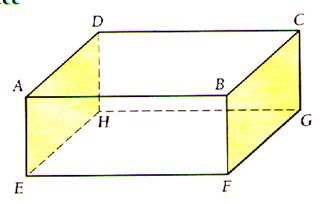
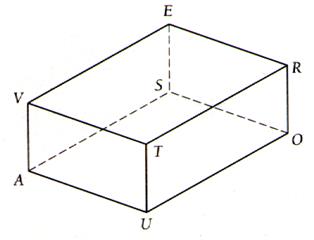
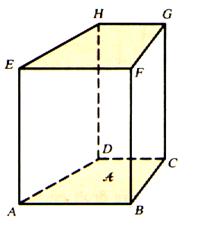
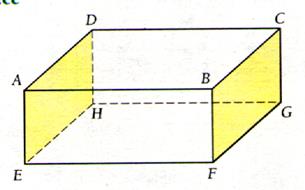
d) Représentation
en perspective d’un prisme ( parallélépipède )
1°) en
Perspective cavalière
|
2° ) en Perspective axonométrique |
|
|
Remarques : en dessin
artistique on utilise les perspectives coniques.
Exemple de représentation d’un prisme :
|
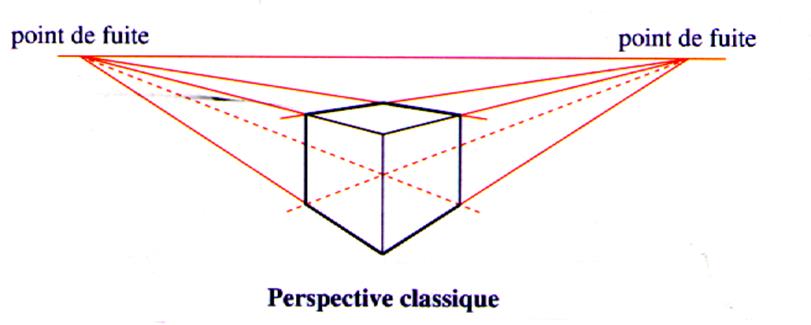
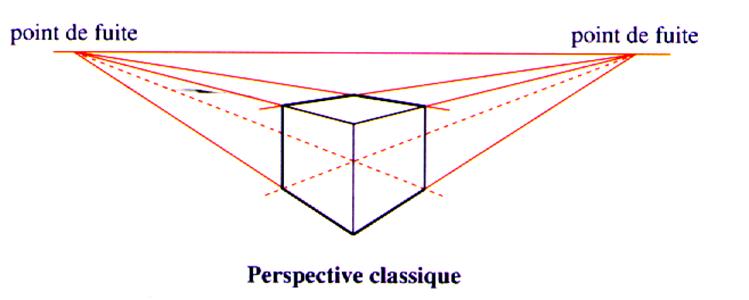
3°) Représentation en perspective
conique d’un parallélépipède en prenant un point de fuite . |
|
|
|
4°) Représentation en perspective
conique d’un parallélépipède en prenant
deux points de fuite . |
|
|
e) Autres représentations en perspective.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS :
1°) Nommer
deux perspectives linéaire utilisés en mathématique pour représenter des
solides ?
2°) Quel principe est utilisé pour chacune
d’elle ?
1°)
Sur une feuille ( 210 / 297 )divisée en deux
parties ,dessiner une boite d’allumettes en perspective cavalière et
perspective axonométrique.
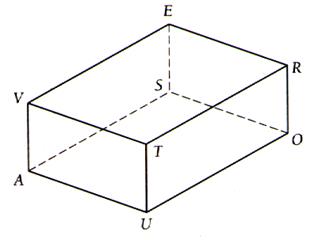
2°))Soit un
prisme représenté en perspective :
Pour chaque cas dites quelle est la
perspective que l’on a utilisé pour représenter ces
prismes :
|
N°1 : |
|
|
N° 2 |
|
|
N°3 |
|
|
N°4 |
|
3°) Dessiner un cube d'arête 5 cm en perspective
cavalière avec l'angle µ = 30° et k = 0,4.