|
|
||
|
|
||
|
|
||
|
|
||
ENVIRONNEMENT du dossier:
|
Objectif précédent : 1.
Le
parallélépipède :
découverte 2.
Fiche
pédagogique 6ème collège : découverte des parallélépipèdes……. |
Objectif suivant |
1°)Informations
sur les calculs des volumes des prismes droits. a)
parallélisme. |
|
|
|
|
|
|
|
|
|
|
|
LE
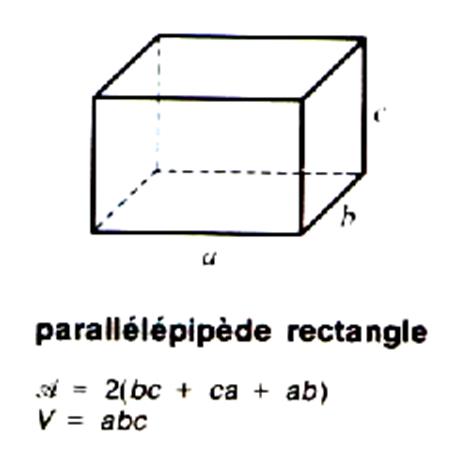
« PARALLELLEPIPEDE RECTANGLE »
ou « prisme rectangulaire » ou « pavé droit » .
1°) Les
faces parallèles et orthogonales ( notions)
2°) ORTHOGONALITE
et PARALLELISME de deux plans ..
3°) Calculs :
· Surface latérale
· Volume.
|
TEST |
COURS |
Devoir
Contrôle |
Devoir évaluation Autres
travaux |
|
|
Corrigé Contrôle |
Corrigé évaluation |
|
|
|
|
Travaux niv VI et V: |
Autres
travaux : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
COURS
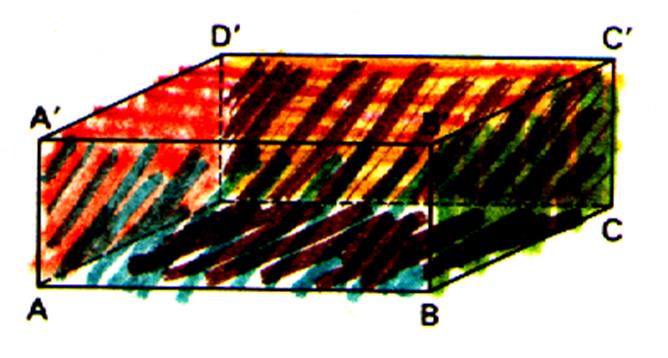
Par définition :
Un parallélépipède rectangle est un prisme droit dont les bases
sont des rectangles .
|
Exemples : la
boite d’allumettes, une brique, la salle de classe, la règle graduée, l’aquarium ,le plateau de la table. Le parallélépipède rectangle ( appelé aussi pavé droit) est un solide limité par six
faces rectangulaires. |
|
|
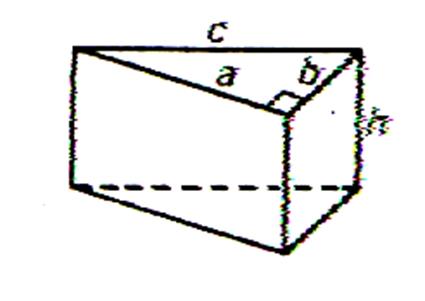
(ici : fiche la perspective
cavalière abordée au collège 6ème.) |
|
|
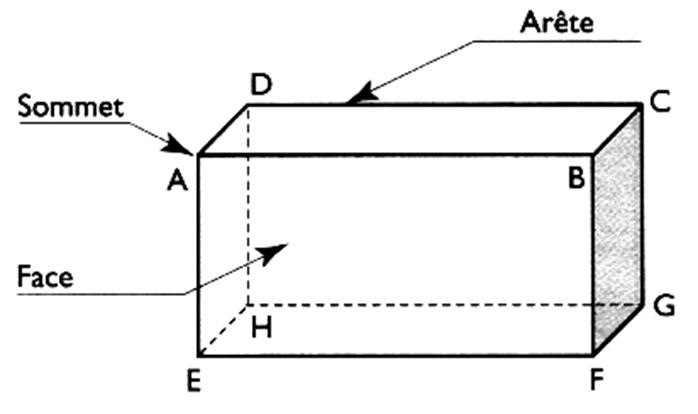
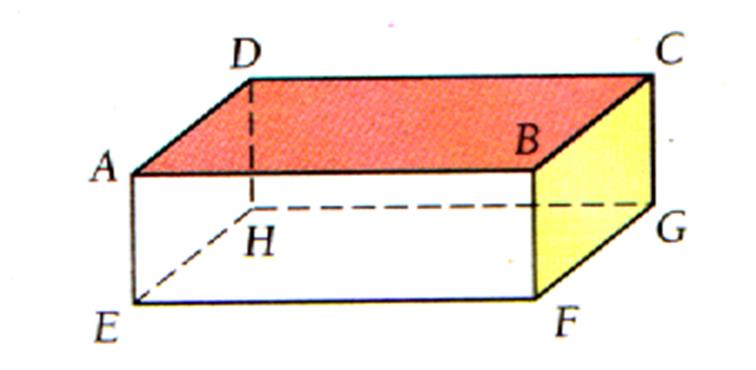
Description : Il possède 6 faces : Les deux faces horizontales sont les
bases. Les quatre autres faces sont dites
« latérales »(l’ensembles des quatre faces
assemblées est appelé : surface prismatique ) Il possède : 8 sommets : A ; B ;C ;D ;G ;H ; E ; F 12 arêtes : ce sont les bords des faces
qui le limitent ,(on dit aussi « intersection de deux plans » ) |
|
|
|
|
Comme pour le cube , les arêtes aboutissant à
un même sommet sont perpendiculaires deux à deux , les faces opposées sont
parallèles deux à deux et les faces ayant
une arête commune sont perpendiculaires .
Chaque face étant un rectangle , les arêtes
opposées d'une même face sont parallèles .
|
Propriétés : - Deux faces opposées ont la même aire ; - Deux arêtes opposées sont parallèles et de même
longueur . |
|
|
II ) ORTHOGONALITE et PARALLELISME de deux plans:
a) Plans orthogonaux et plans
parallèles
Remarque : on dira
que : deux plans confondus sont dit « parallèles »
|
OBSERVATIONS : Poser une boite sur une table. |
|
|
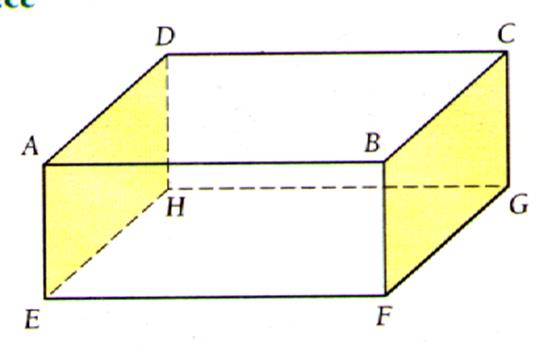
1°) La
face du parallélépipède rectangle
ABCD est parallèle à face du
parallélépipède rectangle EHGF. 2°) La
face du parallélépipède rectangle ABCD
est orthogonale à la face DCGH |
|
b) Les faces
parallèles dans un parallélépipède rectangle :
|
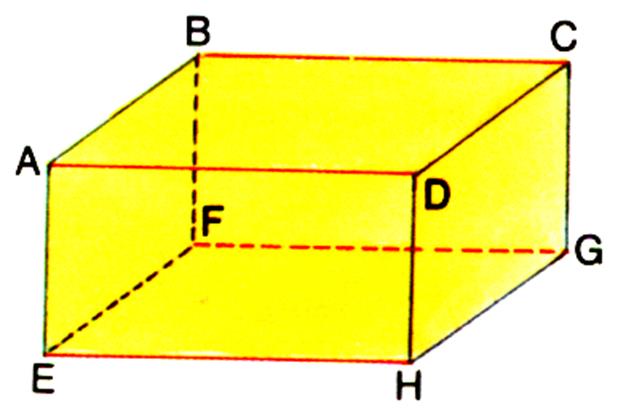
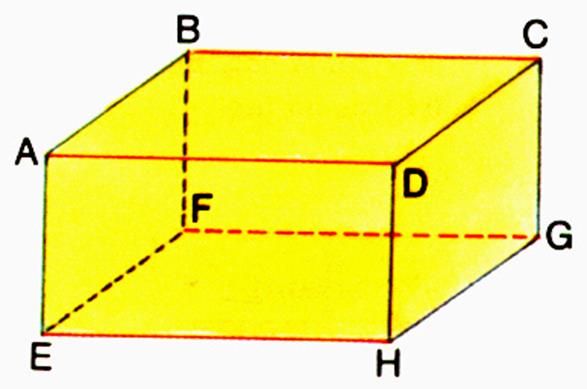
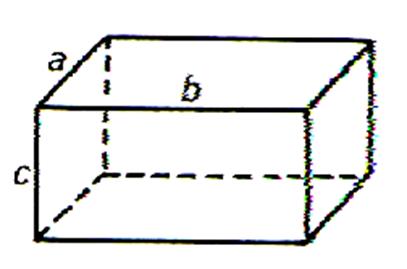
Soit le parallélépipède rectangle ci –dessous : |
|
|
Les faces sont parallèles deux à deux . : La face ADCB est parallèle à la face EHGF. La face ADHE est parallèle à la face BCGF La face ABEF est parallèle à la face DCGH. Les faces nommées en « premier » sont
appelées « faces » de référence.
|
|
Activité : Identifier les
faces parallèles entre – elles : ( mettre une croix
lorsque les deux faces sont parallèles )
|
|
ABCD |
DCGH |
GHEF |
FEAB |
ADHC |
BCGF |
|
ABCD |
|
|
|
|
|
|
|
DCGH |
|
|
|
|
|
|
|
GHEF |
|
|
|
|
|
|
|
FEAB |
|
|
|
|
|
|
|
ADHC |
|
|
|
|
|
|
|
BCGF |
|
|
|
|
|
|
c) Les faces perpendiculaires (
orthogonales) dans un parallélépipède rectangle :
Dictionnaire : deux faces sont
orthogonales si elles forment un angle droit .
.
|
Dans un parallélépipède rectangle une face à 4
faces perpendiculaires . La face du parallélépipède rectangle ADCB est orthogonale à la face BCGF |
|
|
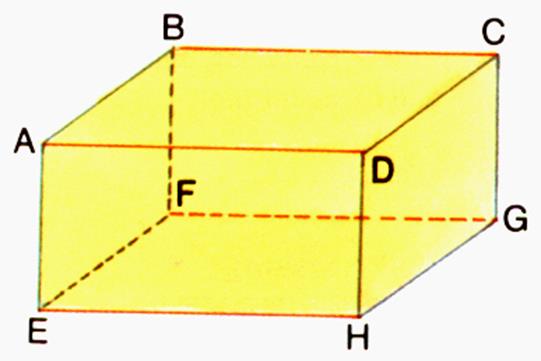
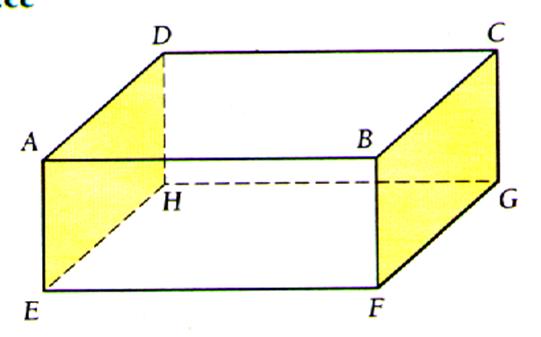
Soit le parallélépipède
rectangle ci - dessous
|
Identifier les faces perpendiculaires entre – elles : ( mettre une croix
pour indiquer que les faces sont perpendiculaires)
|
|
ABCD |
DCGH |
GHEF |
FEAB |
ADHC |
BCGF |
|
ABCD |
|
|
|
|
|
|
|
DCGH |
|
|
|
|
|
|
|
GHEF |
|
|
|
|
|
|
|
FEAB |
|
|
|
|
|
|
|
ADHC |
|
|
|
|
|
|
|
BCGF |
|
|
|
|
|
|
Interdisciplinarité : EN TECHNOLOGIE :
Par convention la face
d’appui est la plus surface en appui
est appelée « première surface de référence » :
La face de référence ( ou
surface de référence) est la face EHGF.( on
l’appelle SR1 en construction mécanique)
|
Parallélépipède rectangle : |
|
|
Les faces sont parallèles deux à deux . : La face ADCB est parallèle à la face EHGF. La face ADHE est parallèle à la face BCGF La face ABEF est parallèle à la face DCGH. Les faces nommées en « premier » sont
appelées « faces » de référence.
|
|
Remarques :
Dans un parallélépipède rectangle il y a trois surfaces de référence ; elles
sont perpendiculaires entre elles . Elles servent de
départ de mesure des dimensions de chaque côte ou
dimensions situant la position de chaque
point du volume considéré. .
Le parallélépipède rectangle est toujours l’enveloppe ( voir les plans
enveloppants en perspective)de solides géométriquement simples ou compliqués .
Ses dimensions sont les dimensions d’encombrement du solide considéré ( les
technicien diraient : dimensions hors tout )
|
On appelle « pavé droit » un
parallélépipède rectangle . C’est un solide limité par six rectangles qui en
sont les faces. On dit que deux faces sont opposées si elles
n’ont aucun point commun. |
|
|
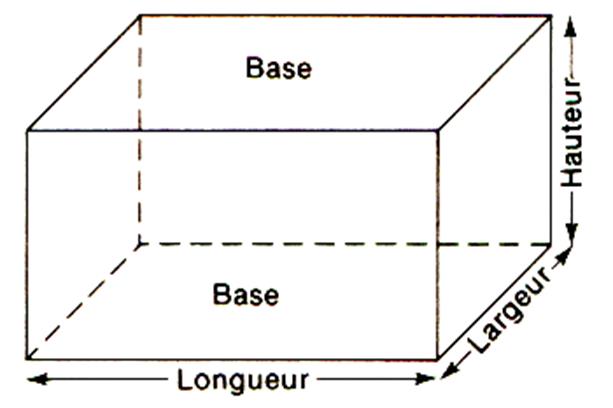
Les dimensions du parallélépipède rectangle sont : La longueur. La largeur La hauteur
( appelée aussi : épaisseur) ; La hauteur est le nombre qui mesure la distance entre deux bases du
parallélépipède. |
|
Développement d’un prisme : ( INFO plus : Développement )
Exemple :
On appelle « développement d’un prisme »
le dépliage des six faces , mis à plat de ces 6 faces sur une surface plane
|
|
|
Calcul du VOLUME du
parallélépipède droit :
|
Pré requis
« l’unité de
volume » On désigne : La Longueur :
« a »
La Largeur : « b » La Hauteur ou
profondeur : « h »
D’où la formule : V =
L Remarque : toutes les dimensions doivent être exprimées dans la
même unité de longueur ,avant d ‘effectuer un
calcul ! |
|
|
Application : |
Exemple : |
|
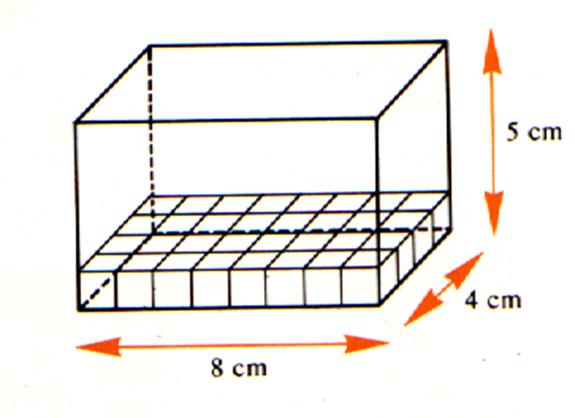
Le volume du parallélépipède rectangle est égal
aux produits de la longueur par la largeur par la hauteur
.(les dimensions sont obligatoirement exprimées dans la même unité de
longueur) Exemple : V = 8 fois 4 fois 5 V = 160 cm3 (lire : |
|
|
Si vous voulez en savoir
plus sur les calculs de volume cliquer ici!!: |
|
Autres calculs :"cubage"
Enoncé :
Un panneau de bois mesure
Réponse :
On pose : V = L
l h ou V
= L
l ép.
a) on
convertit dans le même unité ( en cm) : 1,92 m= 192 cm ; par
V = 192 par
75 par 2,8
V = 40320 cm3
V = 0 ,
Le résultat exprimé en m3 au cm3 prés cela donne : V = 0 ,
Et exprimé en
m3 au dm3 prés cela donne : V = 0 , 0403 m3
Si vous avez
un problème de compréhension sur les arrondis ; voir le cours « arrondir et troncature »
TRAVAUX AUTO
FORMATIFS.
CONTROLE :
Donner la définition d’un parallélépipède rectangle
.
EVALUATION
1°) Faire une représentation graphique ( dessiner)
un parallélépipède rectangle en perspective cavalière .
2°)
|
Calculer : - la longueur d’une diagonale - l’aire de la surface latérale - l’aire totale - le volume du parallélépipède droit avec les données suivantes : a = b = c = |
|
3°)
|
Calculer : - la longueur d’une diagonale - l’aire de la surface latérale - l’aire totale - le volume du parallélépipède droit avec les données suivantes : a = b = c = h = |
|
INTERDISCIPLINARITE : voir : dossier 219