Pré requis:
ENVIRONNEMENT du dossier:
|
Objectif précédent 1°)les positions de plans dans l’espace 2°)La
sphère |
DOSSIER « GEOMETRIE DANS L
ESPACE »:
I ) LES POLYEDRES (définition et classification)
II) LES POLYEDRES REGULIERS.
III) Le « TETRAEDRE ».
|
TEST |
COURS
|
|
On
retiendra :
1. Polyèdre. — On appelle polyèdre tout solide limité par des polygones plans
ayant deux â deux un côté commun.
2. Polyèdre convexe. — Un polyèdre est convexe lorsqu’il
est tout entier d’un même côté du plan de chacune de ses faces
.
3. Polyèdre régulier. — Un polyèdre convexe est
régulier lorsque toutes ses faces sont des polygones réguliers égaux.
On
démontre que les angles polyèdres d’un tel polyèdre sont égaux entre eux de
même que ses angles dièdres.
On
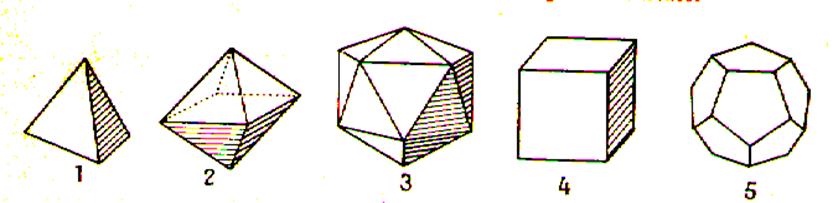
démontre aussi qu’il existe seulement cinq polyèdres réguliers : le tétraèdre
régulier limité par 4 triangles équilatéraux égaux, l’hexaèdre régulier ou
cube limité par 6 carrés égaux, l’octaèdre régulier limité par 8
triangles équilatéraux égaux, le dodécaèdre régulier limité par 12
pentagones réguliers égaux et l’icosaèdre régulier limité par 20
triangles équilatéraux égaux.
COURS
|
|
I
) LES POLYEDRES |
|
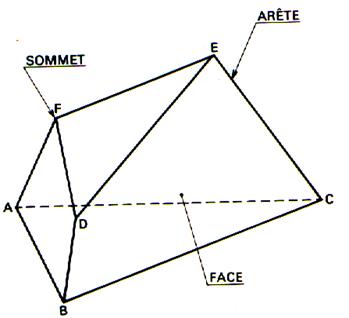
Définition : Polyèdre :
un polyèdre est un solide limité par des polygones plans (faces) ,ayant deux à deux un côté commun On dit qu’il est
« convexe » lorsqu’il est tout
entier d’un même côté du plan de chacune de ses faces et par
rapport à n’importe qu’elle face .
Caractéristiques du
Polyèdre
|
Un
polyèdre est un solide limité par des plans. Ces plans sont appelés :
« faces » du polyèdre ( exemple ABC ;
BDEC ; FDE ;ACEF) L’intersection de deux de ses faces s’appelle « arête » (exemple :
AB ;BD ; BC ;..) Les points de rencontre de ses arêtes se nomment « sommets »
(exemples : A ;B ;c etc..) |
|
Un polyèdre est un
solide borné de toutes part par des facettes planes. Exemple : un cube , une pyramide.
Nous ne considérerons guère que des polyèdres « convexes » , c’est à dire tels que chaque facette ne soit traversée
ni par une autre facette ni par une autre facette ni par le prolongement
d’aucune autre .
Il existe cependant des polyèdres concaves et des polyèdres enchevêtrés.
Eléments
principaux d’un polyèdre.
Dans l’étude d’un polyèdre il y aura lieu de considérer :
1°) le nombre F des « facettes » ; chaque facette est un polygone dont on observera la nature ( triangle
, quadrilatère , etc. ) ;et parfois la forme spéciale ( parallélogramme ,
polygone régulier, etc. )
2°) le nombre A des « arêtes » ;chaque
arête est l’arête d’un dièdre , dont la grandeur est
parfois remarquable (dièdre droit notamment ) ;
3°) le nombre S des sommets : chacun est le sommet d’un angle polyédral : on appelle
ainsi la figure formée par les arêtes
aboutissant au même sommet , arêtes dont on
pourra compter le nombre.
4°) les diagonales et plans diagonaux. Une
diagonale est un segment , autre qu’une arête ,
joignant deux sommets du polyèdre. On pourra distinguer les diagonales de facettes , joignant deux sommets d’une même facette , et les
diagonales libres. Les plans diagonaux sont les plans contenant trois sommets
(ou davantage) n’appartenant pas à une même facette.
Les
polyèdres convexes et concaves :
Un polyèdre est convexe lorsqu’il est tout entier d’un même côté du plan
de chacune de ses faces. (le tétraèdre est un polyèdre
convexe.)
|
|
|
Dans le cas contraire le polyèdre est « concave ».
|
|
|
|
Les faces d’un polyèdre convexe sont des polygones convexes car elles
sont situés en entier dans l’un des demi - plans limités par chacun de leurs côtés. On
voit de même que les sections planes d’un polyèdre convexe sont des polygones
convexes.
Une droite ne peut couper la surface qui limite un polygone convexe en
plus de deux points , sinon tout plan passant par
cette droite couperait ce polyèdre suivant un polygone concave.
Il faut noter que tout polyèdre non convexe peut être décomposé en deux
ou plusieurs polyèdres convexes.
Classification
des polyèdres.
Un polyèdre a au moins quatre faces car trois plans ne limitent pas un
solide. On classe les polyèdres d’après le nombre de leurs faces.
Une première classification se base sur le nombre des facettes ;
d’après ce nombre , voici les noms donnés aux
polyèdres les plus usuels :
|
Tétraèdre (4
faces et 4 sommets) |
|
|
Pentaèdre (5 faces et …….sommets ) |
|
|
Hexaèdre (parallélépipèdes ) (6 faces , 8 sommets) |
|
|
Octaèdre (8 faces et 6 sommets) |
|
|
Dodécaèdre (12 faces et 20 sommets) |
|
|
Icosaèdre (20 faces et 12 sommets) |
|
Cette classification est insuffisante, et devra être complétée en tenant
compte de la nature des facettes .
►Polyèdres de
forme spéciale.
Nous considérerons trois classes de polyèdres :
Les prismes , et notamment les « parallélépipèdes » ;
Les pyramides ;
Les polyèdres réguliers.
Cette
dernière n’exclut pas les autres , car deux polyèdres
réguliers sont des variétés de prisme ou de pyramide.
|
|
II
) Les
polyèdres réguliers. |
|
Définition : On appelle
« polyèdre régulier » un polyèdre dont toutes les faces sont des
polygones réguliers égaux , et dont tous les dièdres sont
égaux. Tous ses angles polyédraux sont égaux.
On démontre qu’il existe seulement cinq polyèdres réguliers :
-
le tétraèdre régulier limité par 4 triangles équilatéraux égaux,
-
l’hexaèdre régulier ou cube limité par 6 carrés égaux,
-
l’octaèdre régulier limité par 8 triangles équilatéraux égaux,
-
le dodécaèdre régulier limité par 12 pentagones réguliers égaux et
l’icosaèdre régulier limité par 20 triangles équilatéraux égaux.
Construction. Sur
papier il faut dessiner des polygones réguliers égaux juxtaposés, et , par des pliages, chercher à construire des polyèdres
réguliers convexes.
Polyèdres à facette triangulaires ;
Autour d’un sommet
« S » peuvent s’assembler :
1°) Trois triangles équilatéraux, cet assemblage, complété par un 4ème
donne un tétraèdre régulier.
|
Les
polyèdres réguliers |
|
|
Intérêts des
polyèdres réguliers :
outre
leur intérêt théorique , signalons que :
1°) on trouve dans les êtres vivants : des petits animaux
microscopiques ont des formes très exactes d’octaèdres ,
de dodécaèdres et d’icosaèdres.
2°)On les trouve dans le règne minéral :
les cristaux d’alun font de parfaits octaèdres réguliers.
3°)leurs multiples symétries les font employer
comme motifs de décoration.
4°) le cube , l’icosaèdre sont employés dans
certains jeux (dés , etc.)
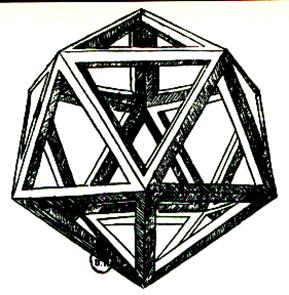
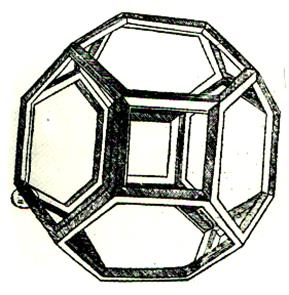
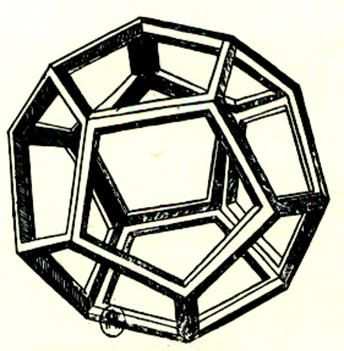
Exemples de polyèdres réguliers et semi -réguliers
dessinés par Léonard de Vinci le De Divina proportione
du mathématicien italien Fra Luca Pacioli .
|
|
|
|
|
|
BN. Roger-Viollet
|
III
) Le
tétraèdre. |
||
|
Vue
en transparence |
Vue
de dessus |
Vue
perspective. |
|
|
|
|
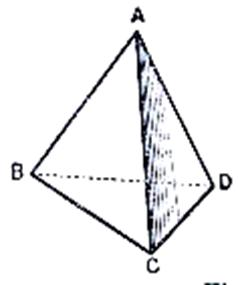
Description :
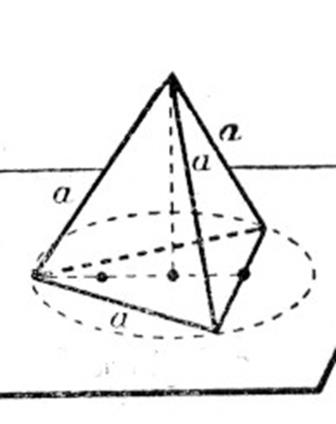
le tétraèdre est un solide borné par 4
facettes planes, et de quatre manières, une pyramide triangulaire.
Il a 4 facettes, qui sont des
triangles ; 4 sommets, qui sont des sommets de trièdres ; et 6
arêtes, deux à deux opposées, aucune diagonale.
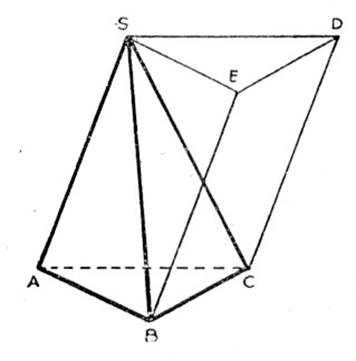
Quelques propriétés du tétraèdre quelconque. Souvent ,
mais pas toujours, les propriétés du tétraèdre rappellent celles des triangles,
et se démontrent de façon analogue.
On s’assurera que :
1°) les six plans médiateurs des arêtes concourent en un même point O,
qui sera centre de la sphère circonscrite au tétraèdre.
2°) Les six plans bissecteurs intérieurs
des dièdres concourent en un même
point « I » , qui sera centre d’une
sphère inscrite.
Il y a aussi des sphères exinscrites, mais elles sont difficiles à
étudier correctement.
3°) les quatre tétramèdianes ( nous appelons ainsi les segments joignant un des sommets
au point de concours des médianes de la facette opposée) concourent en un même
point « G » , situé au quart de chacune d’elles à partir de la base.
Ce point « G » est le centre de gravité de tétraèdre solide homogène.
4°) Par contre, les quatre hauteurs ne se coupent pas
, en général, en un même point : il n’y a pas d’orthocentre.
Tétraèdre
spéciaux.
Voici , entre autres, quelques tétraèdres
remarquables.
1°) Le tétraèdre trirectangle, qu’on obtient en tronquant un cube. Un
des trièdres , A, est trirectangle ; la facette
opposée BCD s’appelle « hypoténuse ». IL a quelques propriétés rappelant
celles du triangle rectangle. Toutefois, il n’est pas inscriptible dans une
demi- sphère.
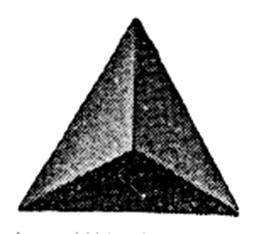
2°)Le tétraèdre régulier, la seule pyramide qui
soit vraiment un polyèdre régulier : ses quatre facettes sont des
triangles équilatéraux ; il a trois axes d’opposition, quatre axes de
rotation à 120°, six plan de symétrie.
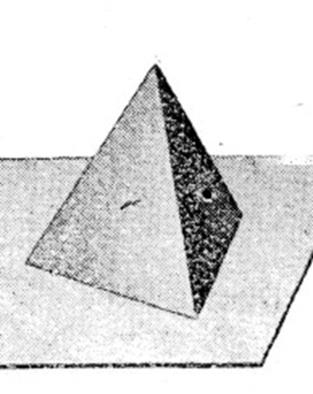
Remarque : pour bien se rendre compte il est conseillé de construire, en papier
fort ou en carton, des modèles de ces divers solides : tétraèdres scalène,
trirectangle, régulier, les arêtes mesurant de 10 à 15 cm . environ.
Observer les images ci dessous :
Elles vont par paire : l’une représente le solide en
« transparence » l’autre
représente le solide « plein »
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
1°) Donner une définition de « polyèdre ».
2°) Quelles sont les caractéristiques d’un polyèdre ?
3°) savoir nommer les polyèdres
réguliers et leurs caractéristiques (nombres de faces et de sommets.)
4°) Qu’est ce qu’un tétraèdre ?
Dessiner en perspective les polyèdres
réguliers.