Pré requis:

POINT LIGNE PLAN

ENVIRONNEMENT du dossier:

Index  « warmaths »

Objectif précédent   Liste des figures géométriques élémentaires

Objectif suivant 1°) quadrilatères 2°) Tracés de polygones  réguliers 3°) les polygones irréguliers 4°) les polygones étoilés 5°) les polygones réguliers (caractéristiques)

tableau    Polygones (2)   Polygones (sommaire)

DOSSIER: LES  POLYGONES  réguliers

1         Liste des polygones réguliers

1         Définitions et axes de symétrie (n°2)    (ici :  info leçon )

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité 1.             les polyèdres 2.       Constructions

Corrigé Contrôle

Corrigé évaluation

 

 

 

Définition de « polygone » : Un polygone est une portion de plan limitée par une ligne brisée fermée.

 

 

 

 

 

 

Info :  COURS

 

 

Définition d’un  polygone régulier

Un polygone est dit « régulier » lorsque tous ses cotés sont égaux ainsi que  tous ses angles . .   Remarque : L ’apothème est le rayon du cercle inscrit.

          Quels que soient ces polygones , pour chaque polygone régulier , leurs sommets peuvent toujours être placés sur un même cercle.

        Pour dessiner un polygone régulier il est commode de tracer le cercle dans lequel il sera « inscrit » ; c’est d’ailleurs une façon de diviser la circonférence en parties égales.

 

 

Les principaux polygones réguliers sont :
Le triangle équilatéral	3 cotés
Le carré	4 cotés
Le pentagone régulier	5 cotés
L’hexagone régulier	6 cotés
L ‘ octogone régulier	8 cotés

 

 

A ceux là s’ajoutent : En cliquant sur les mots vous avez accès à de plus amples informations sur la figure :

 

 

Les polygones   réguliers de plus de 4 cotés
	L’ heptagone	( 7 cotés)
	L’ennéagone	( 9 cotés)
	Le décagone	( 10 cotés)
	Le dodécagone	(12 côtés)

 

Quant aux autres polygones réguliers  , pour éviter l'emploi de termes techniques trop "prétentieux" , on les désigne par le nombre de leurs cotés.             Ainsi l'on dit : un polygone à 7 cotés , un polygone à 11 cotés , un polygone de 15 cotés,…etc.     Un triangle se désigne par trois lettres , un quadrilatère par quatre lettres , et un polygone quelconque par autant de lettres qu'il renferme d'angles.          Il y a dans un polygone  régulier autant d'angles qu'il y a de cotés.

 

 

 

 

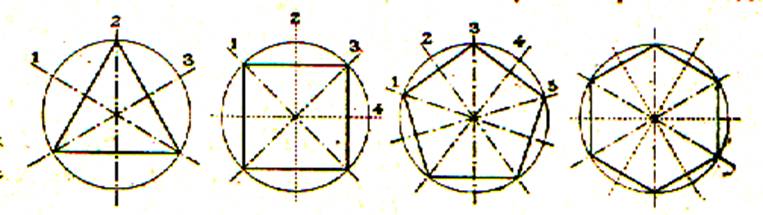
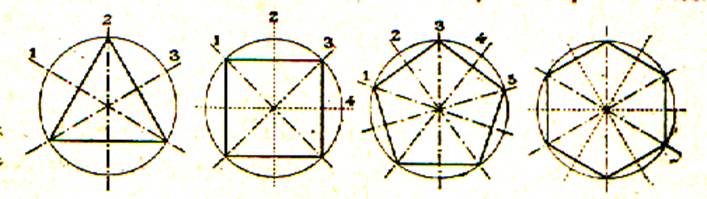
Les polygones réguliers possèdent des axes de symétrie :

 

Exemples

( voir les axes de symétrie dans les polygones réguliers)

      

 

    Un polygone régulier à autant d’axes de symétrie que de cotés.

          

 

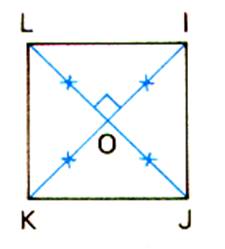
   Si le nombre des cotés est pair ( carré , hexagone) , il y a deux sortes d’axes , les uns portent les rayons ( droites qui joignent le centre du cercle aux sommets du polygones )   , les autres les apothèmes  ( droites  perpendiculaires aux côtés en leur milieu ).  Exemple : l’hexagone ( 6 côtés  a 6 axes de symétrie )

          

 

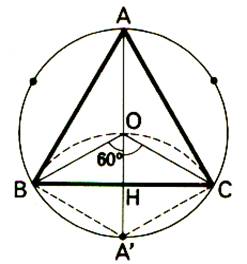
   Si le nombre des cotés est impair (triangle , pentagone) , ces deux sortent d’axes se confondent ;les axes de symétrie sont les perpendiculaires aux côtés en leur milieu .

 

 

Quand le nombre des cotés est pair , le centre du polygone est un centre de symétrie.

 

 

 

INFO sur les calculs du   Périmètre et de l’aire d’un polygone régulier :

 

 

            Pour obtenir le périmètre ou l’aire d’un polygone dont le nombre de côtés est supérieur à 4 côtés il faut décomposer le polygone en figures élémentaires simples ( triangles , rectangle ,carré , cercle ;)    faire le calcul pour chaque figure simple , et ensuite effectuer une addition des valeurs trouvées ( longueurs ou aire élémentaires)

Constructions :

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

Qu’est qu’un  polygone régulier ?

Citer les principaux polygones réguliers ?

Que possèdent – il de particulier ?

 

EVALUATION

 

Nommer les polygones réguliers suivants :