|
|
ENVIRONNEMENT du
dossier:
|
Objectif précédent : |
2°)périmètre de
polygones réguliers 3°) aires de
polygones réguliers . |
||
|
|
|
|
|
DOSSIER : Les caractéristiques
numériques d’un polygone régulier non étoilé .
|
TEST |
COURS |
Interdisciplinarité
|
|
Le polygone régulier et ses
caractéristiques : données numériques relatives aux polygones réguliers , non étoilés
Les rosaces sont des dessins d’ ornementation formés par des arcs de cercle pouvant être
dessinés ou être découpés .
|
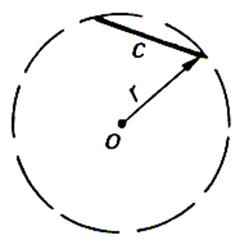
« C » = côté « r » = rayon « O » : centre |
|
|
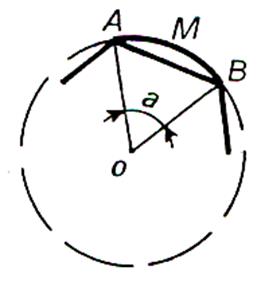
« a » angle au centre .
Angle au centre : on le calcul en divisant 360° par le
nombre de côtés du polygone régulier . |
|
|
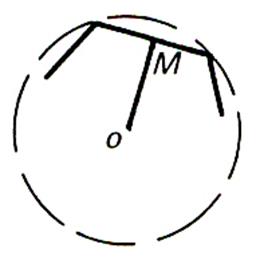
« M » étant milieu
d’un côté ,
le segment OM , qui est perpendiculaire au côté du polygone , est appelé « apothème »
du polygone régulier. |
|
|
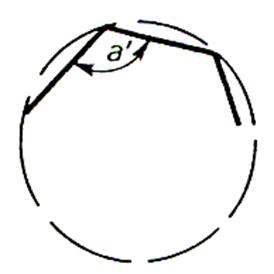
Angle intérieur : c’est l’angle formé par deux côtés
consécutifs. Il égale la somme des On l’obtient donc en
retranchant l’angle au centre de 180°. |
|
Calculs : Tous les calculs relatifs aux polygones réguliers s’effectuent à partir
du triangle rectangle OMA ( centre
« O » , sommet « A » , côté AB , « M » étant le milieu de AB .
TRAVAUX
AUTO- FORMATIFS
CONTROLE :
Quelles sont les caractéristiques numériques d’un polygone régulier non étoilé ?
EVALUATION
Série 1
|
Nommer les polygones de 5 cotés
ou plus |
|
|
5 cotés |
|
|
6 cotés |
|
|
7 cotés |
|
|
8 cotés |
|
|
9 cotés |
|
|
10 cotés |
|
Série 2
|
Combien de côtés ont les polygones suivants |
|
|
Le décagone |
|
|
L’hexagone |
|
|
L’octogone |
|
|
L’ heptagone |
|
|
Le pentagone |
|
|
L’ennéagone |
|