Pré requis:

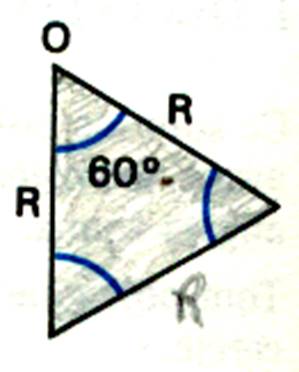
Voir le découpage d’un triangle quelconque en deux triangles rectangles

Quadrilatère convexe et non - convexe

Les polygones

Formulaire ( calcul des aires des figures élémentaires)

ENVIRONNEMENT du dossier:

					Polygones (5)
Index « warmaths »		AVANT : 1°) Aire et surface Notion	COURS	APRES : Liste des objectifs de calculs d’aire 2°) Aire de polygones irréguliers.	Complément d’Info : Sommaire sur : Les calculs d’aires
	DOSSIER : Calculs de l’ AIRE D’UN POLYGONE.

1. Aire d’un Polygone régulier convexe de plus de 4 côtés et Complément :

2. Aire d’un polygone quelconque Polygone irrégulier

Travaux ; devoirs			►►Travaux	Corrigé
TEST	Contrôle	évaluation ►Série de devoir niveau V	►►Et encore  en interdisciplinarité !!!	Contrôle	évaluation

Interdisciplinarités : Situations problèmes (matière concernée)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

2 cas sont a étudier : l’Aire d’un polygone quelconque et aire d’un polygone régulier convexe

COURS

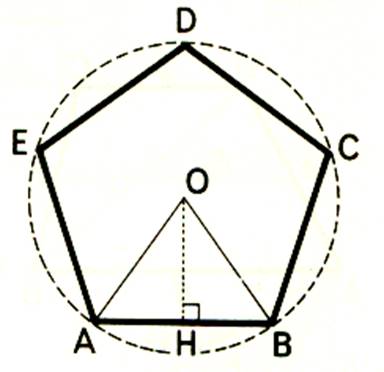
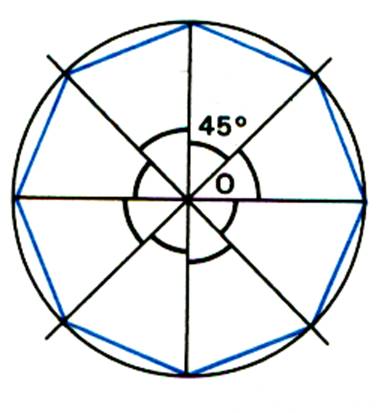
A ) Aire d’un polygone régulier convexe :

Pré requis : aire d’un triangle : L’aire d’un polygone régulier convexe est égale au demi- produit de son périmètre et de son apothème .
exemple : considérons le pentagone régulier ABCDE de centre O et d’apothème OH . Son aire s’obtient en multipliant par 5 celle du triangle OAB . Donc : S = = Or 5 AB est le périmètre du polygone ABCDE. Donc , l’aire du pentagone régulier s’obtient en multipliant le périmètre par la moitié de l’apothème. Il en est de même , quel que soit le nombre des côtés du polygone considéré.	exemple : pentagone
Autre exemple : L’aire de l’hexagone régulier inscrit dans un cercle de rayon R est donc : S = , soit S = (triangle de base)	Exemple : l’hexagone.

B ) Aire d’un polygone quelconque :

L’aire d’un polygone peut être obtenue en effectuant un découpage du polygone en surfaces élémentaires ( Carrés , rectangle , triangle rectangle ,……) La superficie totale s’obtient soit :

par décomposition en surfaces élémentaires et addition des aires

ou par différence ( aire d’un rectangle diminué de la somme des aires exclues)

1°) Par décomposition :

Exemple 1
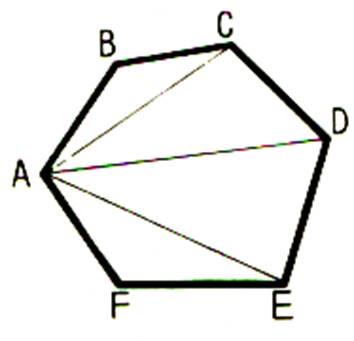
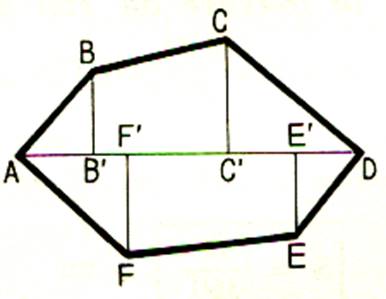
L’aire du polygone ABCDEF est la somme des aires des triangles ABC , ACD , ADE et AEF
Exemple 2
L’aire du polygone ABCDEF est la somme des aires des triangles rectangles ABB’ , CC’D , EE’D , AFF’ et des trapèzes rectangles BCC’B’ et EFF’E’ . Ce procédé est celui utilisé par les arpenteurs.

2° ) Par différence :

Exemple :
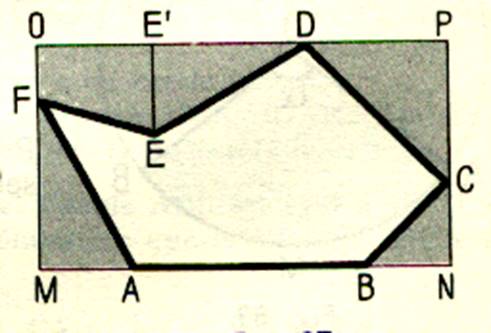
L’aire du polygone ABCDEF est égale à l’aire du rectangle circonscrit MNPQ diminuée de la somme des aires des triangles rectangles BNC , CPD , DEE’ et FMA et du trapèze rectangle EE’QF. Ce procédé est souvent utiliser pour connaître l’aire d’une pièce d’eau .

Calculs d’aires Exercice traités :

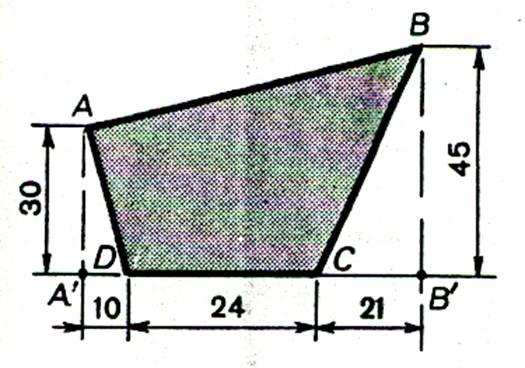
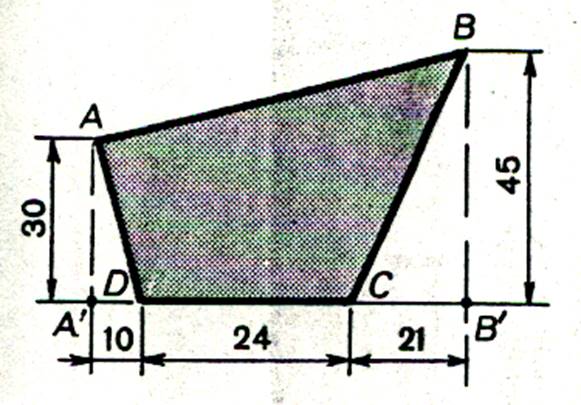
Calculer l’aire de la surface ( ABCD) ; les côtes sont en cm

Aire ( ABCD) = Aire ( AA’BB’) – [Aire ( BB’C) + Aire ( AA’D)]

Aire ( ABCD) = -

Aire = 1440 cm²

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) A quoi est égale l’aire d’un polygone régulier ?

2°) Citer le nom des deux possibilités pour obtenir l’aire d’un polygone quelconque.

EVALUATION:

1°) Faire le découpage suivant deux cas :

- Par décomposition ( clairière)

- Par différence ( pièce d’eau )

N°4

Soit un octogone ; son rayon du cercle = 5 cm. Calculer l’aire de l’octogone .

PROBLEME :

Calculer l’aire de la surface ( ABCD) ; les côtes sont en cm