Pré requis:

Les outils de contrôle
Représentation d’un plan dans l’espace
Deux droites parallèles
Deux droites sécantes

ENVIRONNEMENT du dossier:

Index accueil warmaths

Objectif précédent : 1°) Position d’une droite par rapport à un plan 2°) Voir le cours de collège ( 5^ème) sur l’étude descriptive de l’espace.

Objectif suivant 1°) Plan horizontal et vertical 2°) Le prisme et ses faces parallèles

°info +++) géométrie dans l’espace

DOSSIER :

Position relative de deux plans . « sécants ou parallèles »  (représentation graphique ) et l’angle dièdre .

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Deux plans peuvent être sécants ou parallèles .

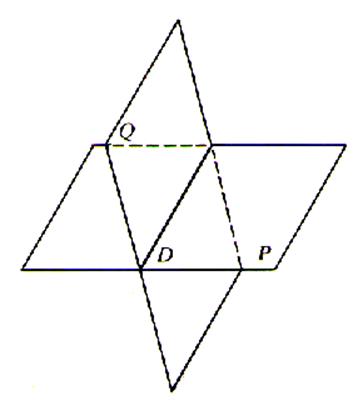
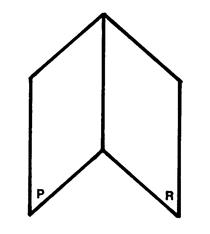
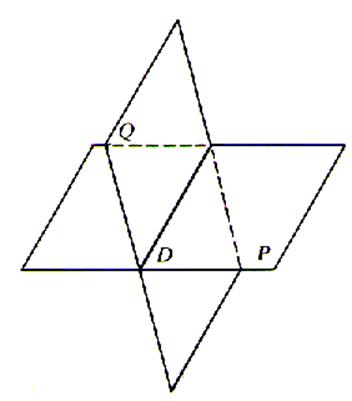
Plans sécants :
Les deux plans sont sécants . Deux plans sont sécants si il ont en commun une droite ( D )
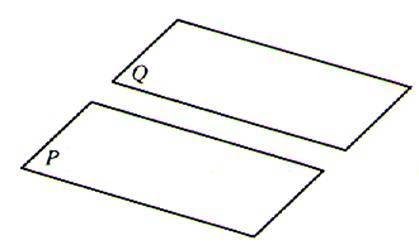
PLANS PARALLELES : Deux plans peuvent être confondus ou disjoints. Deux plans disjoints n’ont aucun point commun .

Deux plans confondus « P » et « Q » ont tous leurs points en commun .

Deux plans sécants se coupent suivant une droite (D)  : Cette droite d’intersection peut être « horizontale ou verticale »

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Compléter les phrases suivantes :

Deux plans peuvent être … …………… .….

Deux plans sécants se coupent suivant ………………….

Deux plans peuvent être ……………………………….

Deux plans confondus ont ………………………….. .

Deux plans disjoints n’ont ……………………………..

EVALUATION:

Représenter deux plans sécantes .

Représenter deux plans parallèles.

Corrigé : CONTROLE:

Compléter les phrases suivantes :

Deux plans peuvent être … sécants ou parallèles .….

Deux plans sécants se coupent suivant une droite

Deux plans peuvent être confondus ou disjoints.

Deux plans confondus ont tous leurs points en commun .

Deux plans disjoints n’ont aucun point commun .