Tableau de conversion dans le système métrique décimal

Index  warmaths.

Objectif précédent  

Le quadrillage

2°) carrelage et découpage

Objectif suivant

Les polygones : rosaces et carrelage

2°) symétrie et pavage

Liste des travaux et leçons sur les calculs d’aires.  

DOSSIER : découpage :  CARRELAGE ET PAVAGE

Mesure des surfaces .

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Les mesures agraires

Corrigé Contrôle  

Corrigé évaluation 

Activités et Travaux niv VI et V

Dossier 132 - 133

COURS

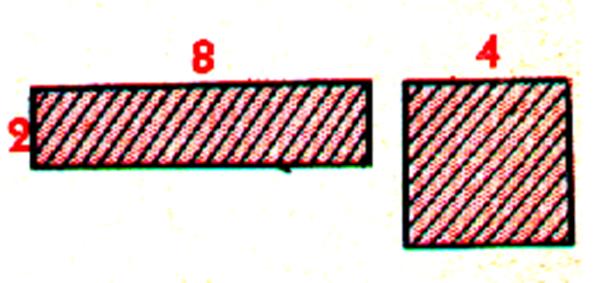
Mais il peut y avoir  des figures qui ne sont pas superposables tout en ayant la même aire , dans ce cas on dit que les deux surfaces sont « équivalentes ».

Soit par exemple , un rectangle ayant 8 cm de longueur  et 2 cm  de largeur et par ailleurs un carré ayant 4 cm  de coté :

Ces deux figures ne sont pas superposables et cependant elles ont la même aire .

Nous dirons que la surface du rectangle est équivalente à celle du carré.

Mesure des surfaces :

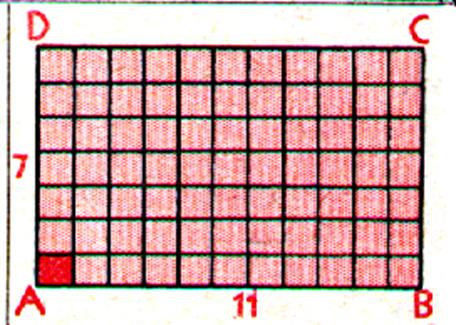
Mesurer une surface , c’est comparer cette surface à une autre surface choisie comme unité.

SOS Cours Conversion d’unités

L’unité fondamentale de longueur étant le mètre , on prend comme unité fondamentale pour  la mesure des surfaces l’aire d’un carré ayant pour coté 1 mètre , cette unité s’appelle le mètre carré.

De même que le mètre a  des multiples et des sous multiples , le mètre carré  a des multiples et des sous multiples.

Pour  rendre plus gai le décor , nous pourrions alterner les couleurs des carreaux ( ce que vous pouvez faire )

Exemples de carrelages

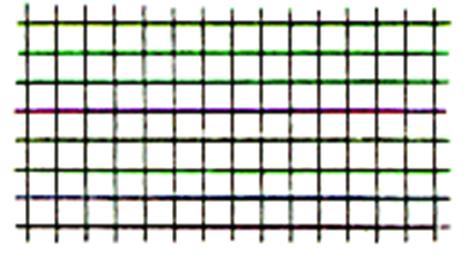
Les figures ci dessous donnent des exemples de combinaisons possibles avec des carreaux ayant la forme  de polygones réguliers .

Compléter les dessins  ci dessous   :

I)  Carrelage avec des carreaux de forme : CARRE

Ce type de carrelage est le découpage retenu pour estimer , ou calculer d’aire d’une surface plane.

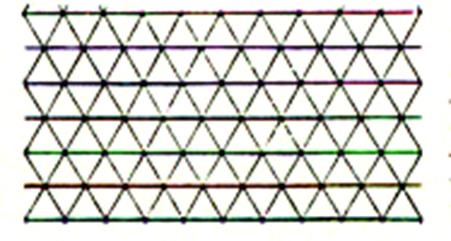
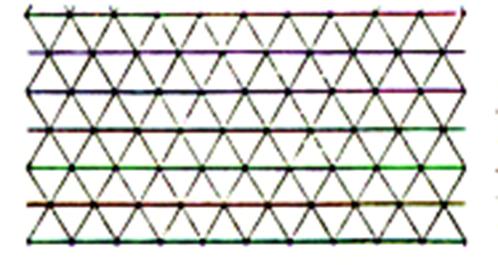
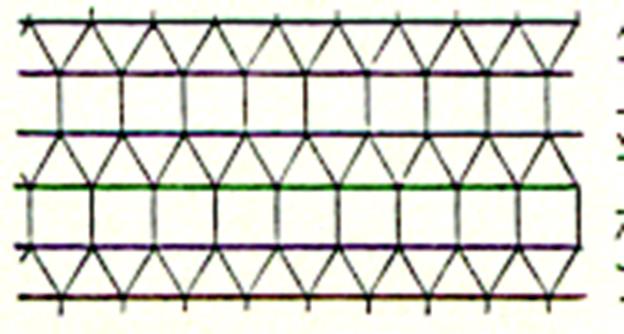
II ) Carrelage avec des carreaux de forme : Triangulaire

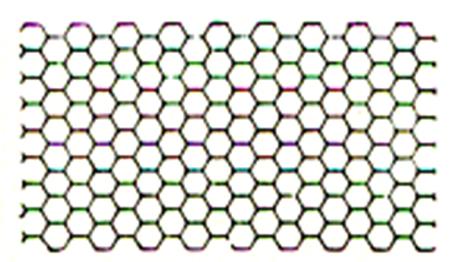
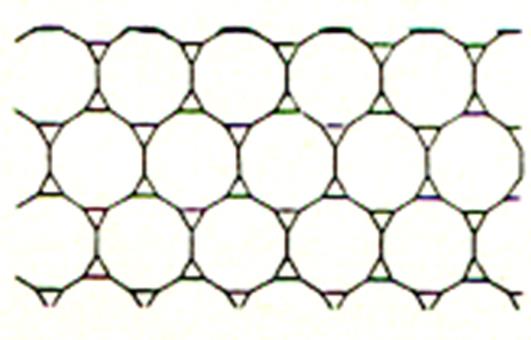
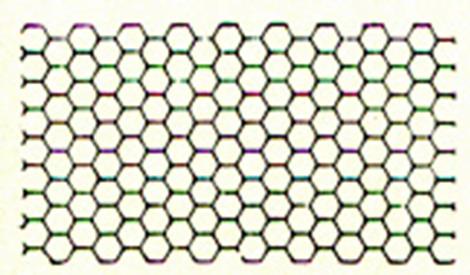
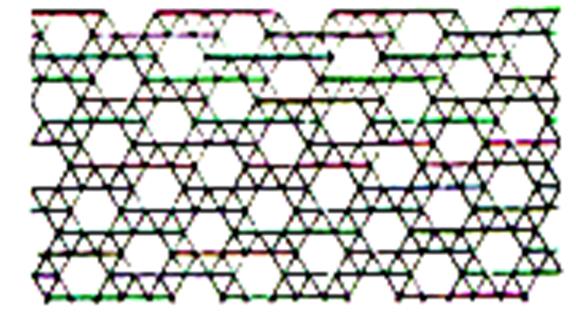
III ) Carrelage avec des carreaux de forme : hexagonale

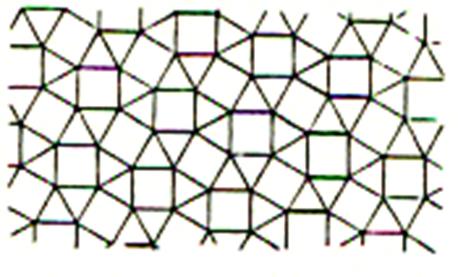
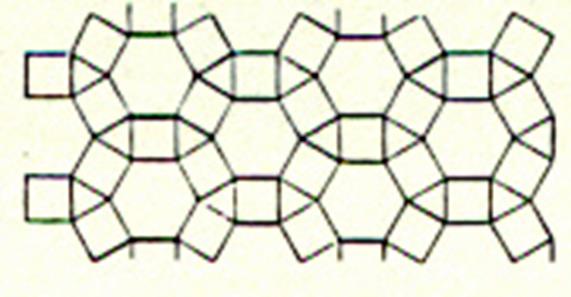
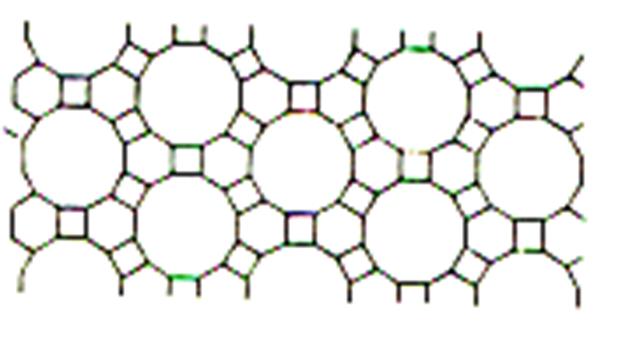
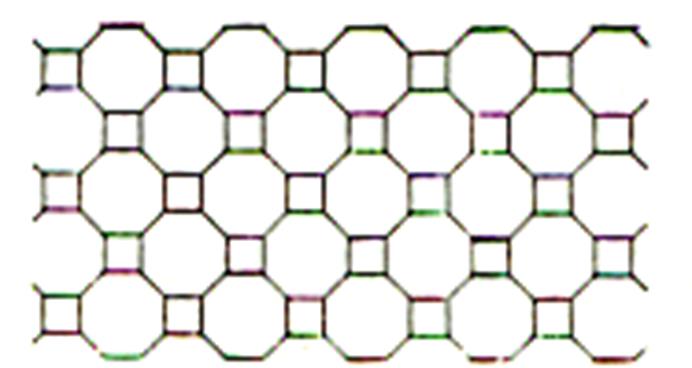
IV  ) Carrelage avec des carreaux de forme : octogonale associer à des carreaux de forme carrée.

PAVAGE DU PLAN . (abordé en 6^e)

( mesure des aires : info plus .)

Un pavage  du plan est un recouvrement de ce plan obtenu à la manière du carreleur : on prend « des pavés » ou « tuiles » que l’on dispose de façon à ce qu’ils s’emboîtent exactement les uns dans les autres . On décide de n’utiliser qu’un petit nombre de modèles.

Les pavages archimédiens :

Si l’on impose seulement aux pavés d’ être des polygones réguliers placés côté à côté  et tels que les configurations autour de chacun de leurs sommets soient toutes identiques , on obtient onze types de pavages . Ces pavages sont appelés « pavage archimédiens »

                Il n’y a  que trois pavages du plan dont les pavés sont tous égaux  à un polygone régulier (on impose aux pavés d’être placés côté contre côté) : ceux associés aux triangles équilatéraux , aux carrés et aux hexagones réguliers.

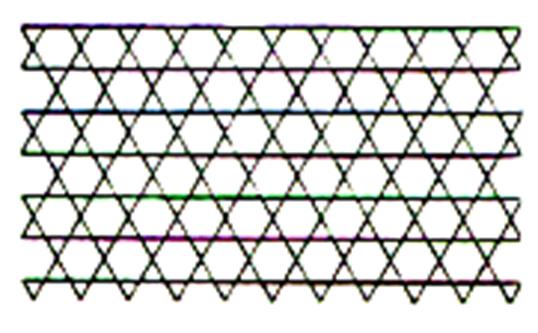
Triangles équilatéraux :

Carrés.

Hexagones .

CONTROLE :

Voir les travaux proposés dossier 132 133.

EVALUATION

INTERDISCIPLINARITE