Pré
requis:
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif
précédent |
Objectif suivant Le pavage
|
DOSSIER
LECTURE : PERMUTATION ET COMBINATOIRE
|
TEST |
COURS |
|
COURS
Le livre des
mutations : l’histoire traditionnelle chinoise attribue le Yi-King
ou livre des mutations au premier des Trois Augustes ,
Fou-Hi inventeur de l’écriture et des
rites du mariage , qui aurait vécu au cinquième millénaire avant notre ère . En
fait , ces textes , qui constituent la base des
philosophies taoïstes et confucianistes , ont vraisemblablement été écrits dans
le courant du premier millénaire avant
notre ère .
La combinatoire peut se définir comme la partie des
mathématiques qui étudie les configurations , c’est à dire les règles d’agencement d’objets en respectant certaines contraintes
.
Ainsi le rangement dans une grande boîte de différents objets de tailles inégales
relève de la combinatoire. Il suffit
d’avoir essayé une fois de remplir le coffre d’une voiture un jour de départ en
vacances pour savoir que ce n’est pas un problème facile .
Il en est de même lorsqu’on essaie de disposer des
nombres dans un carré quadrillé de telle sorte
que la somme des éléments sur la
verticale ou sur une horizontale soit constante . Cela s’appelle un carré magique
, et on en trouve jusque dans
l’un des plus vieux textes de l’histoire
de l’humanité :le Yi-King.
4 9 2 3 5 7 8 1 6
Exemple : Lo–Shu
On dit que ce carré magique est parfait car la somme
De deux nombres situés en position symétriques par
Rapport à son centre est toujours égale au double
du
nombre inscrit au centre :
4+6 = 3+7 = 8+2 = 1+9 = 2 fois 5
D’après la légende , ce
carré magique , appelé Lo–Shu
Emergea de la
rivière Lo porté par une tortue
divine.
Le premier ouvrage sur la combinatoire
, Ars Combinatoire , a été publié
par Leibniz en 1666 .
Mais ce sont Leonhard Euler
et Pierre – Simon de Laplace qui développèrent véritablement la combinatoire
moderne , suivi par William Hamilton , George Polyà , Paul Erdos et bien
d’autres .
C’est un domaine
des mathématiques qui trouve de nombreuses applications dans des
domaines très variés .
Par exemple , en chimie , pour démontrer les
différentes possibilités d’assemblage des molécules entre elles dans les
polymères, ou bine
en gestion et en recherche opérationnelle , pour minimiser les coûts de
fabrication ou pour organiser la
répartition des tâches dans une entreprise .
Entre ces problèmes concrets et le résultat
mathématique qu’on utilise , il y a toute une chaîne
d’étapes pour transformer , résoudre et interpréter le problème de départ .
Pour en donner une idée prenons le
problème des sept ponts de Königsberg , et voyons
comment Euler l’a résolu en 1736
|
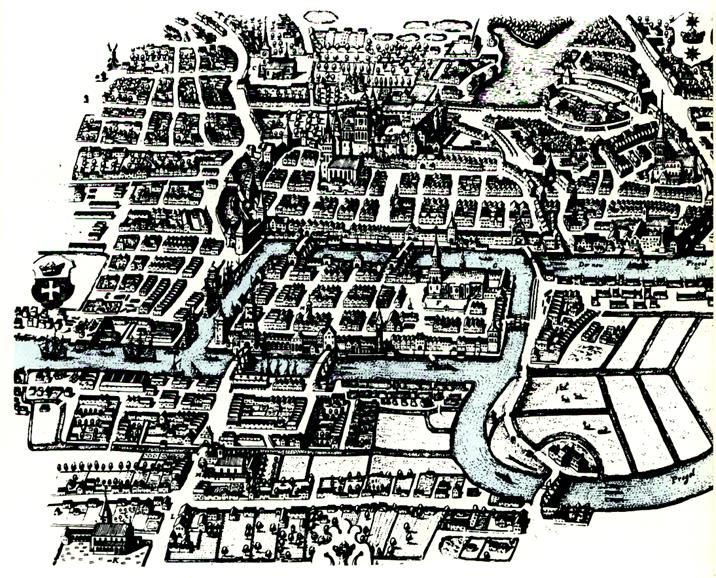
Les ponts de Königsberg : Au début
du XVIIe siècle les habitants
de la ville de Königsberg ( qui s’appelle
aujourd’hui Kaliningrad , située en Union Soviétique ) se posaient un
problème à la fois simple et amusant : Est-il possible de se promener dans le parc de Königsberg en
traversant une fois exactement chacun de ses sept ponts ? |
|
|
|
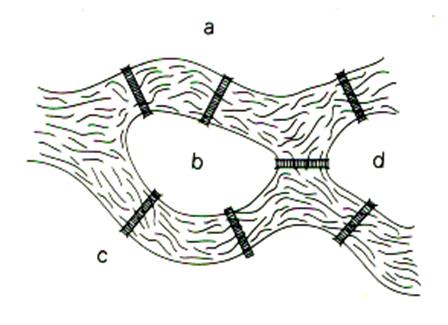
Euler est parti de la remarque suivante :
supposons que l’on observe le trajet d’un habitant de la ville qui
essaierait – comme beaucoup tentaient paraît-il de le faire – de visiter le
parc de Königsberg en empruntant exactement une fois chacun de ses ponts , et comptons combien de fois ce promeneur visite
l’île à laquelle aboutissent cinq ponts. S’il se contente d’une seule visite
, il n’empruntera que deux ponts. De même ,
en deux visites il n’empruntera que quatre ponts . Il doit donc
nécessairement effectuer une troisième
visite de l’île , mais alors il sera contraint de repasser une deuxième fois par l'un des
cinq ponts. Finalement , il est impossible de visiter
le parc de cette façon... |
|
|
|
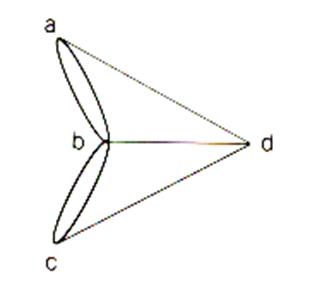
Le problème de Königsberg n’était pas très
important en lui- même , mais il a permit
à Euler
de créer une nouvelle branche des mathématiques , la théorie des graphes
, et d’introduire les outils nécessaires à la résolution des problèmes qui y
sont associés .
Faire
les activités suivantes :