|
¥ |
|
|
Pré requis: |
|
|
¥ |
|
|
Travaux dossier 8 ; dossier 10 |
|
ENVIRONNEMENT du
dossier:
DOSSIER :
1ère
partie : Notion ; établissement d’un tableau
de proportionnalité ;
2ème partie : les tableaux de 4 nombres
proportionnels .
|
COURS
|
Interdisciplinarité : |
|
|||||
|
|
|
|
|
|
|
|
COURS
1ère partie :
Notion ; établissement d’un tableau de proportionnalité ;
Approches :
on sait que : Une rose coûte 3 € .
|
Questions ? |
Réponses : |
|
Combien coûte 2 roses ? |
2 roses coûtent : 3 fois
2 = 6 € ou 3 |
|
Combien coûte 3 roses ? |
3 roses coûtent : 3 fois
3 = 9 € ou 3 |
|
Combien coûte 4 roses ? |
4 roses coûtent : 3 fois
4 = 12 € ou 3 |
|
Combien coûte 5 roses ? |
5 roses coûtent : 3 fois
5 = 15 € ou 3 |
|
Combien coûte 6 roses ? |
6 roses coûtent : 3 fois
6 = 18 € ou 3 |
|
Combien coûte 7 roses ? |
7 roses coûtent : 3 fois
7 = 21 € ou 3 |
|
Combien coûte 10 roses ? |
10 roses coûtent : 3 fois
10 = 30 € ou 3 |
|
Combien coûte 25 roses ? |
25 roses coûtent : 3 fois
25 = 75 € ou 3 |
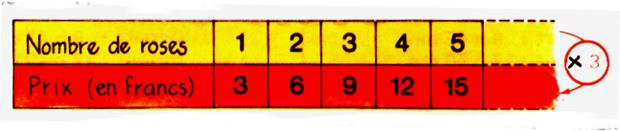
Pour simplifier l’écriture nous allons utiliser un
tableau comportant 2 lignes et autant de colonnes qu’il y a de calculs.
|
|
La première ligne indique le nombre de roses ; La deuxième ligne indique le prix à payer
Informations
importantes :
Pour passer de la première à la deuxième ligne on multiplie chaque
nombre de la première ligne par un même
nombre ; que l’on appelle « coefficient » ( ici le coefficient
multiplicateur est « 3 » )
Inversement , pour passer de le deuxième ligne , je divise le nombre de la seconde ligne par ce même
coefficient ; pour obtenir le nombre de la première ligne.
|
Nombres de roses |
1 |
2 |
3 |
4 |
5 |
6 |
9 |
10 |
25 |
« x » |
® ¿ |
|
Prix ( en
euro) |
3 |
6 |
9 |
12 |
15 |
18 |
27 |
30 |
75 |
|
( 1® 3 ; 2®6 ;3®9 ; ……. ;10® 30 ; 1et 3 ; 2 et 6 ; 3 et 9 ; 10
et 30 ; 25 et 75 ; sont appelés « nombres correspondants »)
Pour chaque situation identique : Les nombres correspondants des 2 lignes sont
dits « proportionnels »
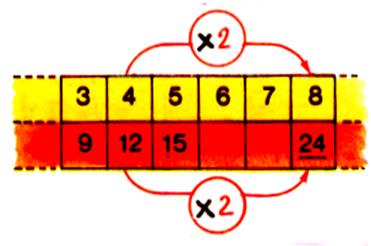
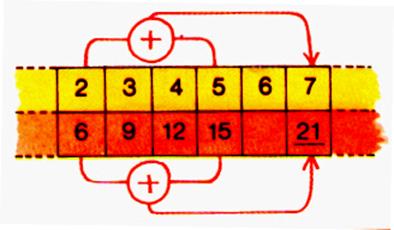
Les exemples suivants montrent comment on peut
utiliser les résultats déjà connus pour calculer , les prix de 8 roses ;
ou de sept roses ;…….
|
Soit en multipliant ! |
Soit en additionnant ! |
|
|
|
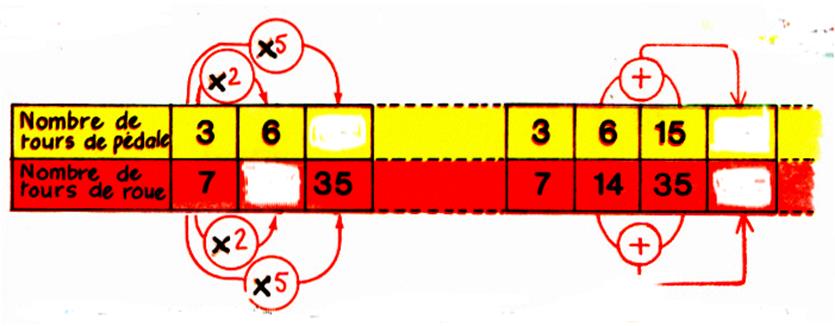
Exemple N°2 de tableau :
Soit un coureur cycliste ; on sait que pour 3
tours de pédale correspondent à 7 tours de roues .
Cette situation est aussi une situation de
proportionnalité :
|
|
|
Compléter le tableau : remplir les cases
« blanches » 6 tours de pédale ® 14 tours de roue ( 7 fois
2 = 14) 35 tours de roue ® 15 tours de pédale ( 3 fois 5 = 15 ) 21 tours de pédale ® 49 tours de roue ( 14 + 35 =
49 ) |
ACTIVITES :
1°) dans la mousse au chocolat , on indique 3 œufs
pour
a- compléter le début du tableau :
|
Nombre d’œufs |
3 |
9 |
12 |
18 |
20 |
® ¿ |
|
Masse de chocolat : ( en g ) |
|
|
|
|
|
b- Prolonger
ce tableau de 2 cases ( comme ci-dessous )
|
Nombre d’œufs |
3 |
9 |
12 |
18 |
20 |
24 |
|
® ¿ |
|
Masse de chocolat : ( en g ) |
120 |
|
|
|
|
|
240 |
Utiliser la première colonne numérique pour remplir
la 7e
Utiliser la 3e colonne pour rempli la 6e
.
2°) On vous donne deux tableaux de nombres . Un
seul est un tableau de nombre proportionnels . Lequel ?
|
a) |
|
b) |
||||||||
|
3 |
7 |
4 |
12 |
15 |
4 |
12 |
7 |
9 |
20 |
|
|
12 |
28 |
16 |
48 |
60 |
24 |
72 |
42 |
58 |
120 |
|
Si l’on modifie un seul nombre de l’autre tableau ,
il deviendra , lui aussi , un tableau de
nombres proportionnels . Recopier ce tableau corrigé .
3°) dans le tableau ci après , on calcule au moyen
de la fonction « …. a ![]() 9 » ou de la fonction inverse ( : 9 ) , les
nombres « a » , « b » , « c », « d » ,
compléter les cases vides .
9 » ou de la fonction inverse ( : 9 ) , les
nombres « a » , « b » , « c », « d » ,
compléter les cases vides .
|
¬ ¯ |
3 |
b |
8 |
7 |
d |
|
¬ : 9 ® |
|
a |
45 |
|
c |
99 |
162 |
4°) dans le tableau ci après
, ( le même que ci dessus) .
On désigne
la première ligne : ligne des nombres « x » ;
On désigne la seconde ligne : ligne des
nombres « y ».
On sait que le nombre « y » d’une colonne
est obtenu en multipliant son nombre correspondant « x » par
« 9 » ; on peut écrire la multiplication y = 9 fois « x »
Travail :
calculer au moyen de la fonction
« x ![]() 9 » ou de la fonction inverse (y : 9 ) , les nombres « a » ,
« b » , « c », « d » , compléter les cases vides
.
9 » ou de la fonction inverse (y : 9 ) , les nombres « a » ,
« b » , « c », « d » , compléter les cases vides
.
|
Ligne des « x » |
3 |
|
8 |
7 |
|
|
¬ : 9 ® |
|
Ligne des « y » |
|
45 |
|
|
99 |
162 |
5°) Un libraire solde des cahiers en les vendant
par lots de « 3 ».Un lot de « 3 » cahiers est vendu 5 €.
Parmi les nombres ci dessous
, encadrer ceux qui peuvent désigner un nombre de cahiers achetés par lots de « 3 » .
|
7 ;
10 ; 12 ; 16 ; 18 ; 20 ; 21 ; 25 ; 30 ( voir la table des
…3…….) |
Ecrire dans la première ligne du tableau ci dessous , les nombres que vous avez encadrés ; et
compléter .
|
Nombre de cahiers |
3 |
|
|
|
|
Prix ( en
€) |
5 |
|
|
|
Trouver le prix correspondant à chaque nombre de cahiers achetés .
6°) Des pamplemousses sont vendus par sachets de
« 6 » , au prix de 2€ le sachet . En utilisant un tableau du modèle ci dessous
, calculer :
-
le prix de 12 pamplemousses ,
-
le nombres de pamplemousses achetés avec 8 €
Utiliser les colonnes déjà remplies pour calculer
le prix de 42 pamplemousses .
|
Nombre de pamplemousses |
6 |
12 |
|
42 |
|
Prix (en euro) |
10 |
|
40 |
|
II )
Proportionnalité : 2e partie : les tableaux de 4
nombres proportionnels .
( SUITE : Info
plus :: le
produit en croix )
A )
Recherche des propriétés :
|
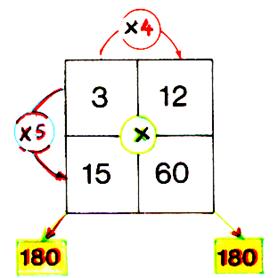
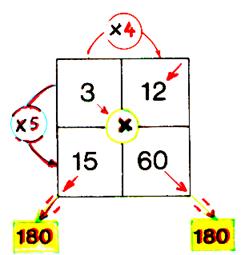
1°) Les nombres « correspondants » des
2 rangées sont proportionnels. (
12 :4 = 3 ; 60 : 4 =
15) 2°) Les nombres
correspondants des 2 colonnes
sont proportionnels : ( 15 :5 = 3 ; 60 : 5 = 12 ) . |
|
|
3°) Les « produits « en croix »
sont égaux
|
Info plus :: le
produit en croix 3
fois 60 = 180 12 fois 15 = 180 conclusion : 3 |
A retenir : Pour vérifier qu’un carré de 4 nombres est un carré de nombres
proportionnels , il suffit de vérifier l’une des trois propriétés ci- dessus .
B) Activités :
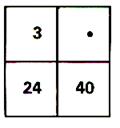
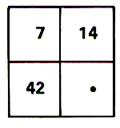
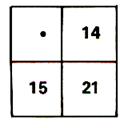
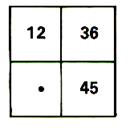
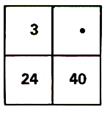
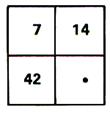
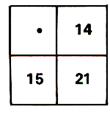
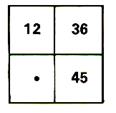
1°)Ecrire le nombre convenable dans la cave vide de
chacun de ces tableaux pour que les nombres correspondants soient
proportionnels.(2° : mettre un nombre au hasard et vérifier qu’il n’y a
pas proportionnalité)
( indiquer comment vous avez obtenu le nombre
cherché )
|
|
|
|
|
2°) Pour faire une citronnade , il faut mettre 5
morceau de sucre avec le jus de 2
citrons .
|
Nombre de citrons |
|
|
|
|
Nombre de morceau de sucre |
|
|
|
Placer dans le tableau les informations ci-dessus .
On doit presser
6 citrons , remplir le tableau , indiquer combien de morceau de sucre on
devra utiliser de morceaux de sucre.
J’ai assez de citrons pour faire 8 citronnades ; remplir le tableau .
3°) On achète 12 rosiers par lots de 3 pour 54 €. Construire un tableau ,pour lire
le prix de 3 ; 6 ; 15 , 18 ,
21 , 42 rosiers .
CONTROLE :
1°) Dans un
tableau de proportionnalité qu’appelle – t – on
« nombres correspondants » ; utiliser un exemple
numérique pour vous aider .
2°) Construire un tableau de proportionnalité .
EVALUATION INTERDISCIPLINARITE
1°) Dans la mousse au chocolat , on indique 3 œufs
pour
b- compléter le début du tableau :
|
Nombre d’œufs |
3 |
9 |
12 |
18 |
20 |
® ¿ |
|
Masse de chocolat : ( en g ) |
|
|
|
|
|
b- Prolonger
ce tableau de 2 cases ( comme ci-dessous )
|
Nombre d’œufs |
3 |
10 |
12 |
15 |
20 |
24 |
|
®
|
|
Masse de chocolat : ( en g ) |
120 |
|
|
|
|
|
2400 |
Utiliser la première colonne numérique pour remplir
la 7e
Utiliser la 3e colonne pour rempli la 6e
.
2°) On vous donne deux tableaux de nombres . Un
seul est un tableau de nombre proportionnels . Lequel ?
|
a) |
|
b) |
||||||||
|
3 |
7 |
4 |
12 |
15 |
4 |
12 |
7 |
9 |
20 |
|
|
12 |
28 |
16 |
48 |
60 |
24 |
72 |
42 |
58 |
120 |
|
Si l’on modifie un seul nombre de l’autre tableau ,
il deviendra , lui aussi , un tableau de
nombres proportionnels . Recopier ce tableau corrigé .
3°) dans le tableau ci après , on calcule au moyen
de la fonction « …. a ![]() 9 » ou de la fonction inverse ( : 9 ) , les
nombres « a » , « b » , « c », « d » ,
compléter les cases vides .
9 » ou de la fonction inverse ( : 9 ) , les
nombres « a » , « b » , « c », « d » ,
compléter les cases vides .
|
¬ ¯ |
3 |
b |
8 |
7 |
d |
18 |
¬ : 9 ® |
|
a = |
45 |
|
c |
99 |
162 |
4°) dans le tableau ci après
, ( le même que ci dessus) .
On désigne
la première ligne : ligne des nombres « x » ;
On désigne la seconde ligne : ligne des
nombres « y ».
On sait que le nombre « y » d’une colonne
est obtenu en multipliant son nombre correspondant « x » par
« 9 » ; on peut écrire la multiplication y = 9 fois « x »
Travail : calculer au moyen de la fonction « x ![]() 9 » ou de la fonction inverse (y : 9 ) , les nombres « a » ,
« b » , « c », « d » , compléter les cases vides
.
9 » ou de la fonction inverse (y : 9 ) , les nombres « a » ,
« b » , « c », « d » , compléter les cases vides
.
|
Ligne des « x » |
3 |
|
8 |
7 |
|
|
¬ : 9 ® |
|
Ligne des « y » |
|
45 |
|
|
99 |
162 |
5°) Un libraire solde des cahiers en les vendant
par lots de « 3 ».Un lot de « 3 » cahiers est vendu 5 €.
Parmi les nombres ci dessous
, encadrer ceux qui peuvent désigner un nombre de cahiers achetés par lots de « 3 » .
|
7 ;
10 ; 12 ; 16 ; 18 ; 20 ;
21 ; 25 ; 30 |
Ecrire dans la première ligne du tableau ci dessous , les nombres que vous avez encadrés ; et
compléter .
|
Nombre de cahiers |
3 |
|
|
|
|
|
Prix ( en
€) |
5 |
|
|
|
|
Trouver le prix correspondant à chaque nombre de cahiers achetés .
6°) Des pamplemousses sont vendus par sachets de
« 6 » , au prix de 2€ le sachet . En utilisant un tableau du modèle ci dessous
, calculer :
-
le prix de 12 pamplemousses ,
-
le nombres de pamplemousses achetés avec 8 €
Utiliser les colonnes déjà remplies pour calculer
le prix de 42 pamplemousses .
|
Nombre de pamplemousses |
6 |
12 |
|
42 |
|
Prix (en euro) |
|
|
40 |
|
7°)Ecrire le nombre convenable dans la cave vide de
chacun de ces tableaux pour que les nombres correspondants soient
proportionnels.(2° : mettre un nombre au hasard et vérifier qu’il n’y a
pas proportionnalité)
( indiquer comment vous avez obtenu le nombre
cherché )
|
|
|
|
|
8°) Pour faire une citronnade , il faut mettre 5
morceau de sucre avec le jus de 2
citrons .
|
Nombre de citrons |
2 |
|
|
|
Nombre de morceau de sucre |
5 |
|
|
Placer dans le tableau les informations ci-dessus .
On doit presser
6 citrons , remplir le tableau , indiquer combien de morceau de sucre on
devra utiliser de morceaux de sucre.
J’ai assez de citrons pour faire 8 citronnades ; remplir le tableau .
3°) On achète 12 rosiers par lots de 3 pour 54 €. Construire un tableau ,pour lire
le prix de 3 ; 6 ; 15 , 18 ,
21 , 42 rosiers .