Auteur : WARME R.                         Dossier : PROFESSEUR
NOM : ………………………………	Prénom : …………………………..	Classe :…………………..
Année    scolaire : ………………………	Dossier pris le : ……/………/………	Validation de la  formation :    O -  N              Le : …………………………………….. Nom du  formateur  : ……………………
ETABLISSEMENT : …………………………………………..

 

 

 

 

 

DOC .INFO : Professeur ; Formateur

10 / 25

DOC : livre  Elève .Cours  interactifs - et travaux +  corrigés.

Titre : PROPORTIONNALITE (applications)

DOSSIER  N°10 Cours INTERACTIF PROPORTIONNALITE applications : Echelle ; pourcentage ; indice.

Information « TRAVAUX auto formatifs » Cliquer sur  le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU : Formation  Niveau V  (inclus le CAP et CFA)		OBJECTIFS : - Savoir utiliser les connaissances sur les proportionnalités : - Savoir traiter les cas sur les échelles ; les pourcentages et les indices.
	Lire :  Notions

I ) Pré requis:

Lectures importantes :
Quelques définitions en rappel. ! ! ! !	Ÿ
Les opérations sur les fractions.	Ÿ
Les grandeurs proportionnelles	Ÿ
Les notions sur les pourcentages	Ÿ
L'échelle ( le matériel )	Ÿ

II ) ENVIRONNEMENT du dossier :

Index

Objectif précédent :   1°)La proportionnalité et l’application linéaire. 2°)

Objectif suivant : 1°) vie quotidienne. 2°) autres activités interdisciplinaires.  3°) La fonction linéaire. Et ses applications. 4°) Fonction linéaire (généralités)

1°) Tableau synoptique : 2°) Liste des cours  niveau V   3°) La fonction linéaire.

III  )LECON : N°10:     PROPORTIONNALITE applications  .

i 9	1°)  Echelles	Info plus !!! :i
i 9	2°)  Pourcentages	Info plus !!! :i ;Tests de fin de formation.
i 9	3°) Indice.	Info plus !!! :i

V)   INFORMATIONS  «  formation leçon » :

Test	COURS	Travaux  auto - formation.				Corrigé des travaux  auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE voir cas par cas ! ! Cliquer ici  : Série 1 ( échelle) Série  2 ( pourcentage) Série 3 ( indice) Série 4 Sciences  et le premier degré à deux inconnues . Série 5 Proportionnalité et les angles		CORRIGE contrôle:	CORRIGE évaluation :

V )   DEVOIRS  ( écrits):

Devoir diagnostique L tests.	Ÿ
Devoir  Auto  - formatif  (intégré au cours)	Ÿ
Devoir Formatif  « Contrôle : savoir » ;   (remédiation)	Ÿ
Devoir  Formatif  «  Evaluation   savoir faire »  (remédiation)	Ÿ
Devoir sommatif .	Ÿ
Devoir certificatif : (remédiation)	Ÿ

* remédiation : ces documents peuvent être réutilisés (tout ou partie) pour conclure une formation.

 

Travaux niveau VI et V   : Echelles	Travaux niveau VI et V : pourcentage	Travaux niveau VI et V   : indice
I► Voir le cours spécifique sur « échelles »	►  voir  au bas du sommaire sur les a%.	I►Voir le cours sur les indices »!
► prendre et faire le :  Dossier 141	Prendre et  faire :  Dossier   198

 

 

Leçon	Titre
N°10	PROPORTIONNALITE applications : Echelle ; pourcentage ;indice .

CHAPITRES

1°)  Echelles	Info plus !!!
2°)  Pourcentages	Info plus !!!
3°)  Indice .	Info plus !!!

 

 

i 9

I.                      Les échelles

Info plus ! ! ! !

 

Définition :                                       Le rapport :  est appelé « l'échelle  du plan » .

L’échelle  permet de représenter « la réalité »  avec des dimensions différentes tout en conservant les mêmes proportions.

 

On note « Dp » dimension du plan et « Dr » la dimension réelle .

D'où la formule :    

 

Résultat du calcul :   L ' "échelle" peut être une fraction ou un nombre décimal.

 

+Activité 1 : Mesures sur un plan de maison

 

on donne  le plan d'une maison, l'échelle  est         (Lire : « un cinquantième »)           

 

On peut dire  que :                                       1 cm sur le plan représente 50 cm dans la réalité.

 

Remarque : la fraction 1/50 à pour valeur décimale : 0,02

 

             

Si l'on cherche à savoir la longueur  réelle de la cuisine dont la mesure sur le plan est 9 cm, on peut construire un tableau de proportionnalité.

 

Mesure "réelle" en cm.	50	x   (9 fois 50 )  = 450 cm
Mesure plan en cm	1	9

Le coefficient de proportionnalité "k" est égal à              ( ou  = 0,02 ) 

 

 

 On en déduit l’équation :              y =  x     ;     D p = Dr

 

 

+Activité 2 : Carte routière

Une carte routière est à l'échelle  1 : 50 000  (un cinquante - millième)

On dira que :  1 cm sur le plan représente 50 000 cm dans la réalité .

Rechercher par quelle mesure   sera représentée sur la carte  une portion de route droite longue de 3,5 km .

On  peut convertir  en cm :  3,5 km = 3 500 m =  350 000  cm

Ou l'on peut convertir 50 000 cm  en km  = 0,500 km

 

On peut établir le tableau :

( x)  Mesures réelles en cm	50 000	350 000
(y)  Mesure sur le plan en cm	1	"y"

On en déduit que :               Dp =     Dr         ou            Dp =  0,000 02 Dr

 

Le coefficient de proportionnalité est de  «1/  50 000 » ou de  «0,000 02 »        ;  soit    l ' équation   " y = 0,000 02  x "

 

- A partir du tableau  ci dessus, on peut effectuer le calcul de "x" :

 

Le produit en croix peut s'effecteur à partir  de la proportion :     =

 

 

Soit  " 50 000 y =  350 000 ;  donc  y  = 350 000 / 50 000 "   donc " y =  7  cm "

 

+Activité 3 : Agrandissement

 

Une plaque de métal  de 12 mm de long sur 6 mm de large  a été  dessinée sur plan, le rectangle mesure  6 cm de long et 3 cm de large. Quelle est l'échelle  utilisée ?

 

=Pour calculer l'échelle avec laquelle elle a été représentée, il faut tout d'abord effectuer les conversions pour que les mesures  soient exprimées  dans la même unité (en mm par exemple) :

 

Les dimensions  du  plan  en mm seront : 6 cm = 60 mm et 3 cm = 30 mm.

D’où le tableau :

Mesures réelles en mm	12 mm	6 mm
Mesures "plans"  en mm	60  mm	30 mm

 

L'échelle est le rapport   soit    ;

 

-   l'échelle utilisée pour  tracer le plan est de "5"

Remarques :

- La valeur du rapport  de l'échelle est supérieure à 1 ; il s'agit  donc d'un agrandissement.

 

-          Le coefficient de proportionnalité est égal au rapport   

-           

On établit la formule, à utiliser :     Dp =  5 Dr    ; (égalité de la forme     y = 5 x)

 

(Voir suite de la leçon : agrandissement ou réduction)

 

II.      Les pourcentages

Info plus 1!!!! ;     Info N°2 +++

 

iPré requis : multiplication d'une fraction par un nombre.

 

Le rapport de deux grandeurs exprimées dans la même unité peut s'écrire sous forme de pourcentage :

 

"je dépense 25 € sur 100 €  ; se traduit par "je dépense 25% de mes 100 €" ;              *

 

Les 25 % de mes 100 € se traduit par l'opération :  = =  = 25

 

Ainsi        25%   =   = 0,25

 

 

+Activité 1 : Rechercher l'existence  d'un "k"  en vu d'obtenir  un  "a % "

 

Lors d'une période de soldes , un commerçant a affiché , pour chaque article  , le prix habituel  et le montant de la réduction  accordée :

 

Marchandise	prix habituel	réduction
Chemise	40 €	10 €
Pantalon	36 €	9 €
Veste	100 €	25 €
Polo	8 €	2 €

 

Pour vérifier qu'il y a « proportionnalité » , nous allons calculer le « coefficient »  multiplicateur  de chaque marchandise ; pour déduire qu'il existe un coefficient de proportionnalité "k" .

 

On établit le tableau :

Prix normal	40	36	100	8
Montant de la réduction	10	9	25	2

Le coefficient est égal au rapport :

 

Chemise  ;      Pantalon   ;        Veste     ;  Polo

 

On constate  que les coefficients obtenus  sont de même valeur : 0,25

 

Le coefficient de proportionnalité est donc k = 0,25

 

On peut écrire ce rapport  sous la forme  d'un pourcentage  pour signifier que la réduction  est de 25 € pour 100 €  ( voir la veste)

 

On écrira : la remise est  25% du prix habituel .

 

iUn pourcentage  permet de connaître la valeur qui correspond à 100 unités d'une grandeur .

 

Exemples :

 

 

.

 

 

 

+Activité 2 :    On veut retrouver une grandeur dont on connaît la valeur d’un certain pourcentage

 

On fait une remise de 20% sur un meuble. Calculer la valeur de ce meuble sachant que la valeur de ces 20 % représente 540 €.

 

i Si la valeur du meuble était de 100 € la remise serait de 20 €. 

 

Coût du meuble	100	"x"
Remise	20	540

 

D’où la proportion :   ; 

 

En résolvant cette équation il vient :  x =  = 2700

 

Donc le prix du meuble était de   2700 €

 

+Activité 3 : Rechercher le pourcentage d’une remise sur un article dont on connaît la valeur ainsi que la valeur de la remise.

 

Un article dont le prix de départ  est de  360 € est vendu avec une remise de 54 € sur le prix. Quelle serait la remise  pour 100 € marqué ?

 

On établit un tableau : 

Prix marqué	360	100
Remise	54	"x"

 

Proportion obtenue :      

 

En résolvant cette équation il vient :

 

Le pourcentage de remise sur le prix marqué est de 15 %

 

:

 

 

 

i 9

III ) LES INDICES

Info plus !!!

 

 

 

 

 

Un indice donne, à une époque " t _i " ,  ( Lire «  temps initial »)  le prix d'un produit dont le prix aurait été de 100 €  à une époque "t _o"  choisie comme base .

 

 

+Activité 1 :  En 2001, le kilogramme de tomates , est vendu 23,40 F ; en 2000 il était vendu  20 F ; à l'indice 100 ; l'année suivante le même kg de tomate est vendu 23,4 F. Trouver l'indice  d'augmentation .

 

L'indice et le prix d'un produit sont des grandeurs proportionnelles.

 

	An 2000	An 2001
indice	100	"x"
Prix au kg	20	23,40

 

L'indice est égale au calcul :

Soit        I  =    =  117

 

L'indice du prix en 2001 est de 117 .

 

L'augmentation en pourcentage  du prix du kg de tomate est de : 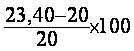  =  17     soit 17%

 

 

+Activité 2

 

En l'an 2001, le kilogramme de tomates, est à l'indice 117 ; en 2000 il était à l'indice 100 ; Cela ne signifie pas qu'en  l'an 2000 le kilogramme de tomates valait 100 F et qu'en 2001 il vaut 117 F.

 

Cela signifie que si le kg de tomates  valait 20 F à l'indice 100 ; le kilogramme vaut en 2001   :    117  = 23,4 F

 

L'indice et le prix d'un produit sont des grandeurs proportionnelles.

 

	An 2000	An 2001
Indice	100	117
Prix au kg	20	????

( R : 23,40)

 

iL'augmentation en pourcentage  du prix du kg de tomate est de :     =  17  soit 17%

 

Leçon	TRAVAUX d ’ AUTO - FORMATION sur
N°10	la PROPORTIONNALITE applications : Echelle ; pourcentage ;  indice .

 

 

A ) Echelle :

1°) A quel  rapport est égal l'échelle  du plan ?

 

 2°) Quand dit-on qu'il y a "agrandissement" ou "diminution"

 

 

B ) Pourcentage :

 

 3°) compléter la phrase :  Pour calculer  " a % " d'une grandeur A , ,on ………………… la grandeur A par  ………. .

 4°) Pour traiter un problème sur les pourcentages on peut utiliser  un tableau …………………………

 

5°) donner la forme du tableau et les informations qu'ils doit contenir:

 

6°) Quelle est la proportion que l'on doit établir  avant de faire un calcul :

 

C) Indice :

 

Commenté cette formule :

I_j/o  =  100

 

 

 

A)  ECHELLES :

 

1°) Sur une carte à l'échelle 1: 20 000, une portion de route mesure 6,5 cm. Calculer la longueur réelle de cette portion de route.

 

2°) Le plan d'un appartement est à l'échelle  1:25 . la longueur réelle de la chambre 1 est 4,50 m. Calculer la mesure  à mesurer sur  le plan.

 

3°) Le dessin d'une pièce de monnaie est à l'échelle 4:3; S'agit - il d'un agrandissement ou diminution ? Calculer la mesure réelle du diamètre  représenté  par 27 mm sur ce dessin .

 

4°) Dans chaque colonne  du tableau , on donne l'échelle et une mesure "plan" . Calculer les mesures réelles correspondantes.

 

Echelles	1 : 2	1 : 20	1 : 125	4 : 3	1 : 1000	3 : 1
Plan	15 mm	8 mm	62 mm	123 mm	7 cm	24 mm
réelles

 

5°) Dans chaque colonne  du tableau , on donne l'échelle et une mesure "réelle" . Calculer les mesures "plan" correspondantes.

 

Echelles	1 : 2	1 : 20	1 : 125	4 : 3	1 : 1000	3 : 1
réelles	15 mm	8 mm	62 mm	123 mm	7 cm	24 mm
Plan

 

B ) POURCENTAGES

 

1°) calcul mental : un commerçant accorde à ses clients une réduction de 15 % sur le prix d'achat . donner dans chaque cas le montant de la réduction : Pour  100 € l'achat la réduction sera de : Pour  200 € l'achat la réduction sera de : Pour  50 € l'achat la réduction sera de :

 

2°) Calculer 24 % de 560 €

 

3°) calculer 3,5 % de 500€

 

4°) Le prix d'un médicament est de 7,8 € . La sécurité sociale rembourse 75 % du prix de ce médicament . Calculer le montant du remboursement.

 

5°) sur une facture, les frais de transport représentent 8 % du prix de la marchandise. Ces frais s'élève à 16 € , calculer le prix de la marchandise.

 

6°) lors d'un examen, 280 candidats ont été admis sur 520 inscrits. Calculer le pourcentage d'admis sur le nombre d' inscrits.

 

7°) un ouvrier gagnait 1256 € par mois, son salaire va être augmenté de 4 %. Quel est le montant de l'augmentation ? et son nouveau salaire.

 

Cliquer ici pour : Exercices  et problèmes supplémentaires

 

 

C) INDICES

 

8°)  Un objet coûtait 2500€ en janvier 1995 ; son prix est passé  à  2550 € en 1996, puis  à 2680 € en 1997 ; 2720 €  en 1998 et 2750 € en 1998.

 

En prenant pour base 100 en 1995, calculer l'indice du prix de cet objet, arrondi à l'unité, pour les 4 années suivantes.

 

9°)  Le propriétaire  d'un appartement utilise le tableau ci - dessous pour calculer le loyer de l'appartement qu'il met en location . Le loyer de cet appartement était en 1994 de 2850 F.

Calculer le montant  du loyer pour les 3 années  suivantes.

 

Année	Indice 4ème trimestre
1994	1019
1995	1013
1996	1046
1997	1068

 

Pour les problèmes  suivants  , on donne la formule suivante  : 

 

10°) Le prix du litre d'essence était à l'époque  t_o de 1,75 €  ; il est de 2,35 € à l'époque  t_n  .Quelle est l'évolution du prix  de l'essence ( en indice) ?

 

 

11°) A une date donnée ( t₁), un objet était vendu 3020 €.

 Un objet de même type vaut 2490 €. 8 ans plus tard (t₂) .

Donner l'indice d'évolution du prix ( diminution ou augmentation).