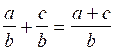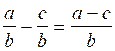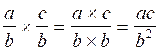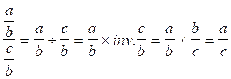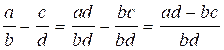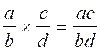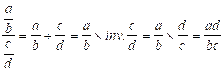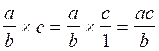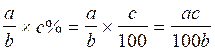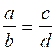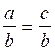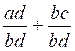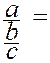|
|
5 / 25 |
|
INFORMATIONS PEDAGOGIQUES :
|
NIVEAU : |
OBJECTIFS : - Savoir faire des calculs avec des fractions de
mêmes dénominateurs
« Addition » ; « soustraction » ;
« multiplication » ; « division ». - Savoir faire des calculs avec des fractions de
dénominateurs différents « Addition » ;
« soustraction » ; « multiplication » ;
« division ». - Savoir faire des calculs avec une fraction et un nombre . .
« Addition » ; « soustraction » ;
« multiplication » ; « division ». |
|
Leçon |
Titre |
|
N°5 |
LES RATIONNELS : Opérations :
Addition ; soustraction ; multiplication ; division |
Important :Pour faciliter
les calculs et pour éviter les risques d’erreurs de calcul , il est
conseillé de simplifier jusqu’à rendre irréductible la ou les
fractions .
PARTIE
1 :
|
|
Contrôle / |
||||
|
SOMMAIRE
Addition , soustraction , multiplication et division |
|
|
|
|
|
|
1.Addition , soustraction
, multiplication et division de deux fractions de même
dénominateur. |
|
||||
|
2.. Addition , soustraction , multiplication et division de deux fractions de
dénominateur différent. |
|
|
|
||
|
3.Addition d’ ‘une fractions et d’un nombre . , soustraction
d’ ‘une fractions et d’un
nombre . |
|
|
|
||
|
4., multiplication d ‘une
fractions et d’un nombre . |
|
|
|
||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|
|
PARTIE 2
I ) Pré
requis 1 : i
liste des travaux de primaire 9
I ) Pré
requis 2:
A ) Les deux
formes de présentation du résultat sont :
|
Fraction irréductible |
|
|
Arrondir "à tant prés" ;troncature |
B ) suite
des pré requis
|
1.
Savoir définir ,reconnaître ,identifier
une fraction : Une fraction est le rapport
(une division )d’un nombre entier naturel par
un autre nombre entier naturel. |
|
|
2.
Savoir simplifier une fraction : Simplifier une fraction c’est diviser le numérateur et le
dénominateur par une même nombre non nul. |
|
|
3.
Savoir
rendre irréductible une fraction : Pour rendre une fraction irréductible il suffit de diviser le
numérateur et le dénominateur par leur PGCD |
|
|
4.
Savoir construire une fraction équivalente à une
fraction donnée : Pour obtenir une fraction équivalente à une fraction donnée il
suffit de multiplier ou diviser le numérateur et le dénominateur de la
fraction donnée par un nombre non nul. Pour vérifier : il faut faire le produit en croix) |
Remarques : Transformations d’une
écriture fractionnaire en fraction
|
Le nombre |
Devient la fraction : |
|
L’écriture fract. |
Devient la fraction : |
|
4 |
= 4 / 1 |
|
1 / 1,2 |
= 10 / 12 |
|
1,5 |
= 1,5 / 1 = 15 / 10 |
|
11 / 1,3 |
= 110 / 13 |
|
2,37 |
= 2,37 / 1 = 237 / 100 |
|
0,54 / 17 |
= 54 / 1 700 |
|
3,673 |
= 3,673 / 1 = 3673 / 1 000 |
|
3,5 / 7,95 |
= 350 / 795 |
II ) ENVIRONNEMENT du
dossier :
|
Objectif précédent : Cd :Cours
précédent ( dossier n° 2) |
Objectif suivant : |
III )
INFORMATIONS « formation
leçon » :
|
|
Travaux auto - formation. |
|
Corrigé
des travaux auto - formation. |
||||
|
|
|||||||
Ce
module sur les opérations est découpé en 5 leçons à étudier distinctes .
Ce
module est long à traiter
, tous les calculs élémentaires (bases)
qu’il aborde sont a connaître et maîtriser .
Il
faut compter en moyenne 2 mois d’études : à raison de :
-
15 jours par leçon . Ce travail
qui doit être conclu par un
devoir ponctuel sur les règles et
calculs élémentaires ; ( soit 1mois et demi )
(voir les travaux auto formatifs ci dessous)
-
les 15 derniers jours sont réservés au travail de synthèse :
chaînes d’opérations avec 3 et plus fractions.
-
Le tout est suivi par un devoir sommatif et des applications interdisciplinaires .
IV ) LES
DEVOIRS ( écrits):
Série 1 ( série particulière qui traite tous les exercices types avec renvois aux
objectifs cours .)
|
|
Série 2 (minimum formation)
|
|
|
|
|
|
|
|
|
|
Devoir
Formatif « Evaluation
1 savoir faire » ( remédiation) |
|
|
Devoir Formatif
« Evaluation 2 savoir faire »
( remédiation) |
|
|
|
|
|
Devoir sommatif
.N°2 |
|
|
|
*
remédiation : ces documents peuvent être réutilisés (
tout ou partie) pour conclure une formation .
|
|
V ) FORMATIONS
SUPPLEMENTAIRES :
|
Leçon ( cliquez
ici pour atteindre les
objectifs de formation) i |
||
|
Opérations avec les écritures fractionnaires |
||
|
Liste
des OBJECTIFS |
Niveau obtenu |
Bilan |
|
Ecriture
fractionnaire :
transformation: |
|
|
|
Savoir
mettre un nombre entier naturel (N ) sous forme de
fraction. |
||
|
Savoir
mettre un nombre entier sous forme de fraction de dénominateur donné. |
||
|
Savoir
représenter un décimal sous forme de fraction (comportant des entiers en
numérateur et dénominateur). |
||
|
Savoir
représenter un décimal sous forme de fraction irréductible. |
||
|
Savoir
remplacer une écriture fractionnaire
par une fraction . |
||
|
Savoir
remplacer une écriture fractionnaire par une fraction irréductible. |
||
|
Savoir
reconnaître et écrire sous forme décimale un nombre décimal qui est
représenté par une fraction. |
||
|
Opérations
avec une fraction et une fraction |
|
|
Opérations
avec une fraction et écriture
fractionnaire |
|
|
Opérations
avec une fraction et un nombre D. |
|
|
Opérations
avec une écriture fractionnaire et une écriture fractionnaire |
Définitions préalables
Fraction : La fraction est le rapport (une division ) d’un nombre entier
naturel par un autre nombre entier naturel
Exemple : 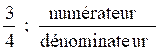
Rationnel Un
rationnel est le quotient
d’un entier par un entier « non nul ». ( on dit
aussi : « différent de zéro » ; noté :
¹ 0 )
Exemples : 16 : 2 = 9 9 est un rationnel
25:
4 = 6,25 6,25 est un rationnel
11
: 7 =
11/7 11/ 7 est un
rationnel
Ecriture
fractionnaire : On
appelle « écriture fractionnaire « une fraction possédant, au moins
un nombre décimal ».( Il y a au moins un nombre
décimal au numérateur ou au dénominateur.)
Pour des raisons « pratiques » il est souvent demandé d'exprimer le
résultat du calcul sous une forme qui vous est précisée:
exemple :« arrondi à …0,001… » ( pour plus d’information consulter le CD : les « nombres irrationnels)
|
Savoir additionner deux
fractions de même dénominateur ;
(cas où les dénominateurs sont différents) |
|
|
Savoir soustraire deux
fractions de même dénominateur ;
(cas où les dénominateurs sont différents)
|
|
|
Savoir multiplier deux fractions de même dénominateur ; (cas où les dénominateurs sont différents) |
|
|
Multiplication :
pourcentage |
|
|
Savoir diviser deux fractions de même dénominateur ; (cas où les dénominateurs sont différents) |
|
|
Savoir diviser un nombre par une fraction |
|
|
Savoir diviser une fraction par un nombre. |