|
Leçon |
CONTROLE |
|
N°5 |
CORRIGE TRAVAUX d ’ AUTO - FORMATION sur LES FRACTIONS et OPERATIONS |
Définitions préalables
1°) donner la
définition d’un fraction : donner un exemple avec 3 et 4
La fraction est le rapport (une division )d’un nombre entier naturel par
un autre nombre entier nature.
2°) Qu’est ce qu’un
rationnel ?
Un rationnel est le quotient d’un entier par un
entier non nul.
Donner des exemples :
16 : 2 = ? 9 ;
9 est un rationnel
25: 4 =
? = 6,25 6 ,25 est un rationnel
11 : 7 =
? = 11/7 11/ 7 est un rationnel
3°) qu’appelle - t -
on « écriture fractionnaire »
On appelle « écriture fractionnaire «
une fraction possédant , au moins un nombre décimal »
|
A. ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de DEUX
FRACTIONS DE MEME DENOMINATEUR . |
|
1. ADDITION |
1°) A quoi est égale la somme de deux fractions ? ( Forme littérale)
La somme de deux fractions est égale à une
troisième fraction qui aura pour « Numérateur » :
la somme des numérateurs et pour « Dénominateur » : le
dénominateur commun .
2°) Donner la Forme symbolique mathématique:
![]()
|
2.SOUSTRACTION |
1°) A quoi est égale la différence de deux fractions de même
dénominateur ? ( Forme
littérale)
La différence de deux fractions est égale à une
troisième fraction qui aura pour
« Numérateur » : la différence des numérateurs et pour
« Dénominateur » : le dénominateur commun.
2°) donner la Forme
symbolique mathématique:
![]()
|
3.MULTIPLICATION |
1°) A quoi est égale la différence de deux fractions de même
dénominateur ? ( Forme
littérale)
La multiplication
de deux fractions de même
dénominateur est égale à une troisième fraction qui aura pour:
« Numérateur » le produit des numérateurs et pour « Dénominateur »
le produit des dénominateurs.
2°) donner sa forme symbolique mathématique:
![]()
|
4 .DIVISION |
1°) Compléter la phrase :
Remarque
importante: Nous ne pouvons pas calculer
directement la fraction de deux fractions ,il faut impérativement transformer
2°) Transformer la fraction de fractions en division de
fractions :
![]() se transforme en
se transforme en ![]()
4°) A quoi est
égale le résultat de la division de deux
fractions de même dénominateur ? ( Forme littérale)
Le
résultat de la division de deux
fractions de même dénominateur est
égale au produit de la première fraction par l’inverse de seconde fraction
.
5° ) montrer
les étapes de transformation conduisant au résultat .
![]() se transforme en
se transforme en ![]() qui devient
qui devient ![]() =
= ![]() =
= ![]() =
=![]()
En conclusion : ![]() =
= ![]()
|
5 .ADDITION : |
1°) Soit les deux fractions ![]() que peut - on
déclarer sur l’addition de ces deux fractions ?: On
ne peut pas additionner des fractions de dénominateurs différents .
que peut - on
déclarer sur l’addition de ces deux fractions ?: On
ne peut pas additionner des fractions de dénominateurs différents .
2°)Ainsi avant de faire l’addition de deux fractions de
dénominateurs différents il faut
transformer chaque fraction en fraction dites « équivalentes » dont le nouveau dénominateur
est « bd » ( le produit des dénominateurs) .
3°) transformer ![]() en fraction équivalente de dénominateur valant
« bd »
en fraction équivalente de dénominateur valant
« bd »
solution : ![]()
4°) transformer ![]() en fraction
équivalente de dénominateur valant « bd »
en fraction
équivalente de dénominateur valant « bd »
solution : ![]()
5 ° ) faire l’addition des
fractions : ![]()
solution : ![]() =
=![]()
|
6. SOUSTRACTION: |
1°) Soit les deux fractions ![]() que peut - on
déclarer sur la soustraction de ces deux
fractions ?: On ne peut pas soustraire des fractions de
dénominateurs différents .
que peut - on
déclarer sur la soustraction de ces deux
fractions ?: On ne peut pas soustraire des fractions de
dénominateurs différents .
2°)Ainsi avant de faire l’addition de deux fractions de
dénominateurs différents il faut
transformer chaque fraction en fraction dites « équivalentes » dont le nouveau dénominateur
est « bd » ( le produit des dénominateurs) .
3°) transformer ![]() en fraction équivalente de dénominateur valant
« bd »
en fraction équivalente de dénominateur valant
« bd »
solution : ![]()
4°) transformer ![]() en fraction
équivalente de dénominateur valant « bd »
en fraction
équivalente de dénominateur valant « bd »
solution : ![]()
5 ° ) faire la soustraction des
fractions : ![]()
On remplace ![]() par
par ![]()
On peut
écrire ![]() =
= ![]()
On peut maintenant effectuer la soustraction des deux fractions: ![]() =
=![]()
|
7.MULTIPLICATION |
1°) à quoi est égale la multiplication de deux fractions
de dénominateurs différents ? (
écriture littérale) ?
La multiplication
de deux fractions de dénominateur
différent est égale à une troisième fraction qui aura pour « Numérateur » : le produit
des numérateurs et pour « Dénominateur » : le produit des
dénominateurs.
2°) donner la traduction
symbolique mathématique: ![]() =
= ![]() =
= ![]()
|
8. DIVISION |
1°) Compléter la phrase :
Remarque
importante: Comme pour la division de deux fractions de même
dénominateur , nous ne pouvons pas calculer
directement la fraction de deux fractions de dénominateur différent , il faut impérativement transformer
2°) Transformer la fraction de fractions en division de
fractions :
![]() se transforme en
se transforme en ![]()
3°) A quoi est
égale le résultat de la division de deux
fractions de même dénominateur ? ( Forme littérale)
Le
résultat de la division de deux
fractions de dénominateur différent est
égal au produit de la première fraction par l’inverse de seconde fraction
.
4° )
montrer les étapes de transformation conduisant au résultat .
![]() se transforme en
se transforme en ![]() qui devient
qui devient ![]() ;
;
En
conclusion : ![]()
![]()
3°) Donner la forme symbolique mathématique du
calcul de ![]() ?
?
solution
|
|
|
C)
ADDITION ; SOUSTRACTION ; MULTIPLICATION ; DIVISION d’
UNE FRACTION et d’UN NOMBRE . |
|
9. ADDITION |
1° ) On ne peut pas
additionner ( ![]() = ?….) une fraction avec un nombre
entier (naturel ou relatif) que faut-il faire pour obtenir un résultat ?
= ?….) une fraction avec un nombre
entier (naturel ou relatif) que faut-il faire pour obtenir un résultat ?
Il
faut transformer l ‘ addition
donnée en addition de deux fractions de même dénominateur.
2° ) Modèle mathématique: ![]() = ?
= ?
3°) donner la procédure à
appliquer pour transformer l ‘ addition
( ou la soustraction ) d’une fraction et un nombre en addition ( ou soustraction) de deux
fractions de même dénominateur en vue faire cette addition ou
soustraction ?.
Solution :
a) Rendre la fraction irréductible.
b) Mettre le nombre sous forme de fraction de dénominateur égal à
1
c) Transformer cette fraction
en fraction équivalente de dénominateur égal au dénominateur de la première fraction.
Modèle mathématique: ![]()
d) Poser la nouvelle égalité :
Modèle mathématique: ![]() =
= ![]()
e) Faire l’addition des deux fractions de même dénominateur.
![]()
f) il
faudra conclure (comme on l’a vu pour les exercices précédents ), après
vérification.
|
10.SOUSTRACTION |
1° ) On ne peut pas
additionner (![]() = ?.) une fraction avec un nombre entier
(naturel ou relatif) que faut-il faire pour obtenir un résultat ?
= ?.) une fraction avec un nombre entier
(naturel ou relatif) que faut-il faire pour obtenir un résultat ?
Il
faut transformer la soustraction
donnée en soustraction de deux fractions de même dénominateur.
2°) donner la procédure à
appliquer pour transformer la soustraction
d’une fraction et un nombre en
soustraction de deux fractions de même dénominateur en vue faire cette
soustraction ?.
solution :
procédure :
a) Rendre la fraction irréductible.:
b)Mettre le nombre sous forme de fraction de dénominateur égal à 1
Modèle
mathématique: c = ![]()
c) Transformer cette fraction
en fraction équivalente de dénominateur égal au
dénominateur de la première fraction.
Modèle mathématique: ![]()
d) poser la nouvelle égalité
Modèle mathématique: ![]() =
= ![]()
e) faire la soustraction des deux fractions de même dénominateur.![]()
f ) il
faudra conclure (comme on l’a vu pour les exercices précédents ), après vérification.
|
11 .MULTIPLICATION |
1°) peut - on multiplier un nombre par une
fraction ?
On ne peut pas
multiplier un nombre par une fraction , pour obtenir un résultat on prendra
appui sur la règle concernant la multiplication de deux fractions.
2°) donner la procédure permettant
de multiplier une fraction par un nombre.
Modèle mathématique: ![]() =
=
a) Placer le nombre sous forme de
fraction de dénominateur égal à 1 : ![]()
b) On passe de ce modèle
mathématique: ![]() à ce modèle
à ce modèle ![]()
c) On applique la procédure
concernant la multiplication de deux fractions:
![]() =
=![]()
d
) Rendre compte: ![]() =
=![]()
|
12. DIVISION |
Etude du 1° cas : « diviser une fraction par
un nombre( entier) »
1°) Donner la procédure permettant de calculer le résultat
de la division d’une fraction par un nombre : ![]()
1°) Première transformation : 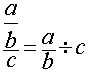
2°) Deuxième transformation 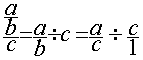
3°) Troisième transformation : 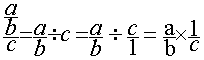
4°) Calcul :
appliquer la règle concernant la multiplication de deux fractions.
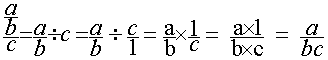
2°)Etude du second cas :
Division d’un nombre "a"
entier par une fraction
Donner la procédure
permettant de calculer le résultat de la division d’un nombre par une fraction: ![]()
a) Transformer la division d’un nombre par
une fraction en une division de fraction
par une fraction. 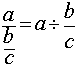
b) Multiplier la première fraction par l
‘inverse de la seconde. 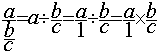
c ) Faire
la multiplication des deux fractions. 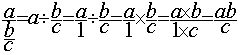
1° a quelle fraction est égale « a% » : a% = ![]()
2°) y = ![]() x ; transformer le deuxième membre y =
x ; transformer le deuxième membre y = ![]() =
= ![]() =
= ![]()
ou « y » est la valeur d’une augmentation ou diminution
« a » la valeur du taux
« x » le nombre sur lequel
s’applique le taux.
|
LECON N°5 |
Devoir : Ÿ Remédiation : Ÿ |
Nom :…………
|
Classe : Groupe : |
|
|
Date :…………… |
Rattrapage : Ÿ Soutien : Ÿ |
Prénom :…………
|
Note
contrôle : |
Note évaluation : |
|
|
Série
1 :
1°) Citer la règle concernant l ‘ addition de deux fractions
de même dénominateur .
2°) Citer la règle concernant la soustraction de deux
fractions de même dénominateur .
3°) Citer la règle concernant la multiplication de deux fractions de même
dénominateur .
4°) Citer la règle concernant la division de deux fractions
de même dénominateur. .
Série 2 :
1°) donner
la procédure à utiliser pour effectuer l
‘ addition de deux fractions de dénominateur différent .
2°) donner
la procédure à utiliser pour effectuer la soustraction de deux fractions de
dénominateur différent ..
3°) donner
la procédure à utiliser pour effectuer la
multiplication de deux fractions de dénominateur différent ..
4°) donner
la procédure à utiliser pour effectuer la division de deux fractions de
dénominateur différent .
Série 3 :
1°) donner
la procédure à utiliser pour effectuer l
‘ addition d’une fraction et d’un nombre
..
2°) donner
la procédure à utiliser pour effectuer la soustraction d’une fraction et d’un nombre
3°) donner
la procédure à utiliser pour effectuer la
multiplication d’une fraction et
d’un nombre
4°) donner
la procédure à utiliser pour effectuer la division d’une fraction et d’un nombre
5°) donner
la procédure à utiliser pour effectuer la division d’un nombre et d’une
fraction.