|
|
|
|
|
|
|
Voir :
relation d’équivalence et partition
d’un ensemble (à faire
) |
|
ENVIRONNEMENT du
dossier:
|
|
AVANT :
1°)L’ensemble N 2°) la fraction décimale , ordinaire et sa conversion exacte ou approchée |
APRES :
|
Complément d’Info :
|
TITRE : L’ensemble des nombres Rationnels noté : Q
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
Interdisciplinarités : (matière concernée) |
||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique |
Physique Chimie Electricité |
Statistique. |
|
COURS
Ensemble des
rationnels :
Approche intuitive : Dans l’ensemble F des nombres fractionnaires
on peut écrire : 
= 
=
=
=
=
;
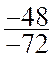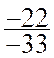etc.
Tous ces nombres peuvent être considérés comme le
même nombre écrit sous des formes différentes . L’ensemble de ces fractions forme une
classe d’équivalence . C’est ce nombre qui est dit
« rationnel » .
Un nombre rationnel peut être représenté par l’une
quelconque de ses formes.
Ainsi représente tous les nombres de la forme 
( k ÎZ*)
L’ensemble des nombres rationnels est donc l’ensemble
quotient de l’ensemble F des nombres fractionnaires par la relation d’égalité . Il se note : ensemble Q .
Dans ce nouvel ensemble il n’existe plus de nombres
différents équivalents entre eux , car tous les
nombres équivalents à forme un seul nombre rationnel .
Pratiquement nous confondrons « nombre
rationnel » et fraction représentative , nous
parlerons par exemple du « nombre rationnel » .
Etude théorique :
Reprenons l’étude de la relation « avoir même valeur » dans F .
= 
Û ad = bc
Elle possède bien les trois propriétés
caractéristiques d’une relation d’équivalence :
Réflexivité : = car :
ad = bc
Symétrie : = Þ =
Transitivité : (1) = et (2)
= 
Þ =
car (1) ad = b c et (2) c
f = de multiplions membre à
membre :
a d c f = b c
d e
Þ a f = e b
Þ =
Cette relation a donc pu , à juste titre être
dite , relation d’ équivalence de deux fractions . Elle détermine les classes
d’équivalences dites : « Nombres rationnels »
Opérations dans l’ensemble des rationnels :
Les opérations : addition ,
soustraction , multiplication , division
( sauf pour le diviseur nul ) possèdent les mêmes propriétés que dans
l’ensemble des nombres fractionnaires .
Représentation d’un rationnel par un nombre
décimal :
Nous savons dans quel cas un rationnel peut être
représenté par un nombre décimal (SOS Rappel ) . Il est alors unique .
Exemple : 
, forme
irréductible : 
;
sa forme décimale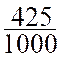 
=
0,425
S’il n’en est pas ainsi la division décimale du numérateur par le dénominateur , donne naissance à une suite décimale illimitée
qui permet , d’avoir des valeurs approchées décimales de ce nombre avec une approximation aussi grande qu’on le désire . ( voir :
encadrement ; arrondir et troncature)
Exemple : « calculer le quotient x
de 
;
exprimer « x » à 10-6 prés par
défaut et par excès
|
17 , 000000 44
280
0,38 63 63 63 …
160
280 période « 63 »
160
…. Ainsi on dire que
« x » est compris entre deux valeurs : 0,386363 et
0,386364
Qui se note :
0,386363 < x <
0,386364 0,386363 est la valeur approchée à 10-6 prés par défaut de « x »
0,386364 est la valeur approchée à 10-6 prés
par excès de « x » d’où l ‘encadrement du
résultat de la division 0,386363 < |
Une suite décimale périodique est une
suite de chiffres appartenant à la partie décimale du nombre décimal et qui se répètent :
Exemple 1 :…,… 63 63 63 … (
67,32 63 63 63 …)
Exemple 2 ; .., 7340 7340 7340…
( 3, 7340
7340 7340…)
On démontre
et nous admettrons que :
1°) Ttout
nombre rationnel donne naissance par division à une suite de décimale
périodique illimitée ( la période étant composée de 0
, dans le cas d’égalité à un nombre décimal )
2°) Sauf pour une suite décimale illimitée de 9 , toute suite décimale illimitée peut
être considérée comme engendrée par un
nombre rationnel .
TRAVAUX AUTO FORMATIFS.
Compléter
les phrases suivantes
1°) tout nombre rationnel donne naissance par division à ………….
2°) Sauf pour une suite décimale
illimitée de 9
, toute suite décimale illimitée peut être considérée …………………………….. .
1°)Quelle est la forme irréductible
du nombre rationnel représenté par :
a ) 
; b)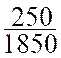 
;
c ) 0,275 ; d) 3,48
( SOS cours)
2°) Quelle est la forme décimale (sans zéro à droite des
chiffres significatifs) du nombre rationnel représenté par :
; 
;
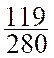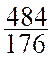
( SOS Cours)
3°) Déterminer la suite décimale périodique engendrée par les fractions
suivantes :
; 
;
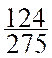
CORRIGE : CONTROLE.
1°) tout nombre rationnel donne naissance par division à une
suite de décimale périodique illimitée ( la période
étant composée de 0 , dans le cas d’égalité à un nombre décimal )
2°) Sauf pour une suite décimale illimitée de 9 , toute suite décimale illimitée peut
être considérée comme engendrée par un
nombre rationnel .
CORRIGE EVALUATION.
1°)
a ) ; (
info procédure)
b) ;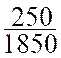
( info procédure)
c )
0,275 ; (info procédure)
d) 3,48 (info procédure )
2°)
= 0,24
=
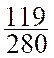0,425 ;
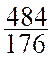= 2,75
3°)
= 0,386363636363636363636363636363636 ;
=
0,621621621621621621621621621621622 ;
=
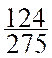0,450909090909090909090909090909091