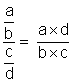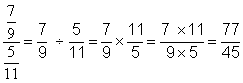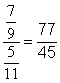|
Auteur :
WARME R.
|
||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|
ETABLISSEMENT :
………………………………………….. |
||
|
|
5 B / 26 |
-Pré
requis : Savoir faire des calculs avec des fractions de mêmes
dénominateurs « Addition » ;
« soustraction » ; « multiplication » ;
« division ». |
||||||||||||||
|
TITRE :
LES FRACTIONS DE
DENOMINATEUR DIFFERENT (Opérations) ADDITION ; SOUSTRACTION ; DIVISION et MULTIPLICATION ; de DEUX FRACTIONS de
DENOMINATEURS DIFFERENTS. |
||||||||||||||||
|
Informations
« TRAVAUX
d’auto - formation » |
||||||||||||||||
|
INFORMATIONS PEDAGOGIQUES : |
||||||||||||||||
|
NIVEAU : |
OBJECTIFS : - Savoir faire des calculs
avec des fractions de dénominateurs différents
« Addition » ; « soustraction » ; « multiplication » ;
« division ». |
|||||||||||||||
|
PREAMBULE
|
||||||||||||||||
|
N°5 |
LES
FRACTIONS DE DENOMINATEUR DIFFERENT (Opérations) |
|||||||||||||||
|
|
|
|||||||||||||||
|
Il faut valider
les acquis précédents avant d’étudier le chapitre « B » (chapitre
suivant). |
|||||||||||||||
|
||||||||||||||||
|
Les fractions sont de la forme :
|
|||||||||||||||
|
1
.ADDITION : de DEUX FRACTIONS de
DENOMINATEURS DIFFERENTS. |
|||||||||||||||
|
|
Soit les deux fractions ► On ne peut pas additionner des fractions de
dénominateurs différents : |
|
|||||||||||||
|
On doit
transformer les fractions en fractions équivalentes dont on donnera un
dénominateur égal au produit des dénominateurs. Ici
le dénominateur commun sera «
bd » |
|||||||||||||||
|
Procédure à respecter pour additionner 2 fractions de
dénominateurs différents. |
|||||||||||||||
|
Activité : « additionner |
|
Exemple : Calculer : |
|||||||||||||
|
Il faut : |
|
|
|||||||||||||
|
1°) Ainsi avant de faire l’addition de deux
fractions il faut transformer
chaque fraction en fraction dite « équivalente »
dont le nouveau dénominateur est égal
au produit des deux dénominateurs « bd » |
|
1°) Ainsi avant de faire l’addition de deux
fractions il faut transformer
chaque fraction en fraction dite « équivalente »
dont le nouveau dénominateur est égal
au produit des deux dénominateurs « 7 fois 11 » soit = 77 |
|||||||||||||
|
2°)
on transforme la première
fraction !
|
|
2°)
on transforme la première
fraction !
|
|||||||||||||
|
3°) on transforme la deuxième fraction !
|
|
3°) on transforme la deuxième fraction !
|
|||||||||||||
|
4°) On
remplace la première addition par l’addition des fractions
équivalentes :
Après
transformations , on se trouve en présence d’une addition de deux
fractions de même dénominateur . |
|
4°) On remplace la première addition par
l’addition des fractions équivalentes :
Après transformations , on se trouve en présence d’une addition de deux fractions de même dénominateur . |
|||||||||||||
|
5°) On
calcule l’addition : On peut
écrire :
On peut
maintenant effectuer l’ addition des deux fractions équivalentes. |
|
5°)
Calcul de l’addition :
l’addition
est rendue possible parce que nous avons deux fractions ayant le même
dénominateur. |
|||||||||||||
|
|
|
|
|||||||||||||
|
Autre
exemple : |
|||||||||||||||
|
Calculer |
|
|
|||||||||||||
|
Procédure à suivre : |
|
|
|||||||||||||
|
1°) Au préalable on
simplifie ou ,dans la mesure du
possible’ on essaie de rendre irréductible la ou les fractions.: |
|
ce
qui est le cas de pour |
|||||||||||||
|
2°) On
remplace l’addition |
|
On a
remplacé |
|||||||||||||
|
3°) On calcule le
« dénominateur commun » : 5 fois 4 = 20 |
|
Il est
égal au produit des dénominateurs. |
|||||||||||||
|
4°) Transformation chaque fraction en fraction équivalente . (Dont le dénominateur sera 20) première fraction : deuxième
fraction : |
|
Vérification : Vérification : |
|||||||||||||
|
5°)
On remplace l’addition avec les fractions de départ par une nouvelle addition
avec des fractions équivalentes : |
|
On dit
que les additions sont équivalentes. Nous avons maintenant
deux fractions de même dénominateur , nous pouvons faire l’addition |
|||||||||||||
|
6°) Calcul de l’addition
et
|
|
|
|||||||||||||
|
7°) Conclusion : |
|||||||||||||||
|
On reprend
l’énoncé : l’addition de
départ ! |
On donne le résultat sous
forme irréductible |
|
|||||||||||||
|
|
|
On peut donner aussi le
résultat sous forme décimale |
|||||||||||||
|
8°) Vérification :
Dans tous les cas il faut vérifier si
notre résultat est conforme ; pour cela
on calcule la division dans chaque fraction : 3/5 = 3 ¸ 5
= 0,6 et
3 / 12 = 3 ¸ 12 =
0,25 |
|||||||||||||||
|
Ensuite
, on remplace les deux fractions par les valeurs décimales calculées
précédemment et l’on compare : |
|
|
|||||||||||||
|
On compare 0,85 avec
|
|||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
2.
SOUSTRACTION: de DEUX
FRACTIONS de DENOMINATEURS DIFFERENTS. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Soit les deux fractions ► On ne peut pas soustraire des fractions de dénominateurs
différents : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On
doit transformer les fractions en
fractions équivalentes dont on donnera un dénominateur égal au produit des
dénominateurs. Ici le dénominateur commun sera
« bd » |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Procédure à respecter pour additionner 2 fractions de
dénominateurs différents. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Activité : « soustraire » dans
le sens a /b - c / d |
|
Exemple : Calculer : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Il faut : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1°) Ainsi avant de faire la soustraction de deux
fractions il faut transformer
chaque fraction en fraction dite « équivalente »
dont le nouveau dénominateur est égal
au produit des deux dénominateurs « bd » |
|
1°) Ainsi avant de faire la soustraction de deux
fractions il faut transformer
chaque fraction en fraction dite « équivalente »
dont le nouveau dénominateur est égal
au produit des deux dénominateurs « 7 fois 11 » soit = 77 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2°)
on transforme la première
fraction !
|
|
2°)
on transforme la première
fraction !
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3°) on transforme la deuxième fraction !
|
|
3°) on transforme la deuxième fraction !
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4°) On
remplace la première soustraction par la soustraction des fractions
équivalentes :
Après transformations , on se trouve en présence d’une
addition de deux fractions de même dénominateur . |
|
4°) On remplace la première soustraction par soustraction
des fractions équivalentes :
Après transformations , on se trouve en présence d’une addition de deux fractions de même dénominateur . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5°) On
calcule la soustraction : On peut
écrire :
On peut
maintenant effectuer la soustraction des
deux fractions équivalentes. |
|
5°)
Calcul de la soustraction :
la
soustraction est rendue possible parce que nous avons deux fractions
ayant le même dénominateur. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Autre
exemple : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculer |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Procédure à suivre : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1°) Au préalable on
simplifie ou ,dans la mesure du
possible’ on essaie de rendre irréductible la ou les fractions.: |
|
ce
qui est le cas de pour |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2°) On remplace la
soustraction |
|
On a
remplacé On obtient une nouvelle soustraction , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3°) On calcule le
« dénominateur commun » : 5 fois 4 = 20 |
|
Il est
égal au produit des dénominateurs. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4°) Transformation chaque fraction en fraction équivalente. (Dont le dénominateur sera 20) première fraction : deuxième
fraction : |
|
Vérification : est « vraie »
parce que dans le produit en croix 3
fois 20 = ( 60) est égal à 5 fois 12 =
( 60) Vérification : est « vraie » parce que 1 fois 20
est égal à 4 fois 5 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5°)
On remplace la soustraction avec les
fractions de départ par une nouvelle addition avec des fractions équivalentes : |
|
On dit que
les soustractions sont équivalentes. Nous avons
maintenant deux fractions de même dénominateur , nous pouvons faire la soustraction
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6°) Calcul de la soustraction : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7°) Conclusion : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On reprend
l’énoncé : l’addition de
départ ! |
On donne le résultat sous
forme irréductible |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
On peut donner aussi le
résultat sous forme décimale |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8°) Vérification :
Dans tous les cas il faut vérifier si
notre résultat est conforme ; pour cela
on calcule la division dans chaque fraction : 3/5 = 3 ¸ 5
= 0,6 et
3 / 12 = 3 ¸ 12 =
0,25 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ensuite
, on remplace les deux fractions par les valeurs décimales calculées
précédemment et l’on compare : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On compare 0,35 avec
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si l’addition et la soustraction de deux
fractions de dénominateurs
différents posent un réel
problème , il n’en est pas de même
pour la multiplication et la division ( ou fraction ) de
fractions : il n’y a
aucune transformation particulière , il faut
appliquer directement les
règles énoncées pour les fractions de même dénominateur . (Voir suite du cours
.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. MULTIPLICATION de DEUX FRACTIONS de
DENOMINATEURS DIFFERENTS. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Il n’y a
pas de transformation particulière à effectuer , ainsi la multiplication
de deux fractions de dénominateur différent ne pose pas de problème particulier . On retiendra la règle suivante : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Règle : (
écriture littérale)La multiplication de deux fractions de dénominateur différent est égale à une
troisième fraction qui aura pour
« Numérateur » : le produit des numérateurs et pour
« Dénominateur » : le produit des dénominateurs. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Traduction
symbolique mathématique |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple : calculer : |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Faire le produit des numérateurs |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Faire le produit des dénominateurs |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
conclusion : |
|
15 / 77 est le résultat : forme irréductible |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Résultat sous forme décimale , 15 / 77 » 0,194805194805194805194805194805195
ce qui peut se ramener au nombre » 0,195 qui est le résultat exprimé à 0,001 prés |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4.
DIVISION de DEUX
FRACTIONS de DENOMINATEURS DIFFERENTS. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
iNous ne
pouvons pas calculer directement la fraction de deux fractions , il faut impérativement
transformer l’écriture |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Donc l’écriture : |
|
se transforme
en :
|
Commentaire : La fraction de fractions
doit être transformée en division de deux fractions. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La fraction de fractions |
|
Commentaire 1: La première fraction étant
au dessus de la barre de fraction
qui se trouve alignée avec le
signe « égal ». |
devient : |
Commentaire 2 : la deuxième fraction étant située sous la barre de fraction alignée avec le signe égal. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Bien que la fraction de fractions soit transformée en
division ; la division de deux fractions ne se fait pas ; il faut
transformer la division en
multiplication en respectant la procédure suivante: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On sait que |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
se transforme en |
qui devient |
En conclusion : Transformation finale |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Commentaire : Première transformation de la fraction de deux fractions en division de deux fractions. |
Deuxième transformation : la multiplication par l’inverse ! |
|
On a transformé la fraction de fractions par une « multiplication » . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Rappel ( Cd ³ ) INVERSE d'un nombre.(ou fraction) : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
l’ inverse de |
|
est égal à |
|
et inv. de |
|
est égal à |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Et l’on applique ,ensuite, les
règles de la multiplication de deux fractions. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Règle : ( forme littérale ) Pour calculer la division de deux fractions il suffit de
multiplier la première fraction par l’inverse de seconde
fraction. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Forme symbolique mathématique : |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple : |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculer : |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
77 / 45 = |
Résultat calculé :( »1,71111111111111111111111111111111) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
conclusion |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
» 1 , 71 à
0,01 près ( il faudrait
faire la
vérification ! !) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+Faire les exercices suivants : |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Addition
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Soustraction ( pour
cet exercice il faut avoir fait la leçon sur les nombres relatifs |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Soustraction |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Multiplication |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fraction de fractions |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Division de fractions |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
iComme vous l’avez remarqué : on
peut multiplier ou diviser directement
deux fractions de dénominateur différent , on ne peut pas additionner ou
soustraire deux fractions qui
n’ont pas le même dénominateur . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Leçon |
Titre |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TRAVAUX
d ’ AUTO - FORMATION sur LES FRACTIONS ( OPERATIONS ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TRAVAUX N°5 B
d ’ AUTO - FORMATION : CONTROLE |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Définitions
préalables 1°) donner la
définition d’un fraction : donner un exemple avec 3 et 4 . Exemples ?: 2°) Qu’est ce qu’un
rationnel ? . Donner des exemples : 16 : 2 = ? ……………………………………………… 25: 4 =
? ……………………………………………… 11 : 7 =
? ………………………………………………… 3°) qu’appelle - t
- on « écriture
fractionnaire » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B ) ADDITION ;
SOUSTRACTION ; MULTIPLICATION ; DIVISION de DEUX FRACTIONS DE DENOMINATEURS DIFFERENTS. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 .ADDITION : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
°) Soit les deux fractions 2°)Ainsi avant de faire l’addition de deux fractions de
dénominateurs différents il faut
transformer chaque fraction en fraction dites « ………………. » dont le nouveau dénominateur est « bd » ( appelé :…………………………………..)
. 3°) transformer 4°) transformer 5 ° ) faire l’addition des
fractions :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6. SOUSTRACTION: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1°) Soit les deux fractions 2°)Ainsi avant de faire l’addition de deux fractions de
dénominateurs différents il faut
transformer chaque fraction en fraction dites « ……………. » dont le nouveau dénominateur est « bd » (appelé :
………………………………) . 3°) transformer 4°) transformer 5 ° ) faire la soustraction des
fractions : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7.MULTIPLICATION |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1°) à quoi est égale la multiplication de deux fractions
de dénominateurs différents ? (
écriture littérale) ? 2°) donner la traduction
symbolique mathématique:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8.
DIVISION |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1°) Compléter la phrase : Remarque
importante: Comme pour la division de deux fractions de même
dénominateur , nous ……………………. calculer
directement la fraction de deux fractions de dénominateur différent , il faut impérativement transformer 2°) Transformer la fraction de fractions en division de
fractions :
4°) A quoi
est égale le résultat de la division
de deux fractions de même dénominateur ? ( Forme littérale) 5° )
montrer les étapes de transformation conduisant au résultat .
3°) Donner la forme symbolique mathématique
du calcul de : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
TRAVAUX N°5
d ’ AUTO - FORMATION : EVALUATION
1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Définitions
préalables |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1°) avec
« 3 » et « 4 »
écrire une fraction ? 2°) souligner
les rationnels . 16 + 2 = 18
; 16 : 2 = 8 ; 16 -2 = 14 25: 4 =
6,25 ; 25 ´ 4 = 100 ; 25 - 4
= 21 11 + 7 =
18 ; 7 - 11 = -4 ; 11 : 7 =
11/7 3°) entourer l ’
« écriture fractionnaire » 16 /
2 ; 17 / 5 ;
20,2 / 2 ; 10 / 0,5 ;
6,3 / 7,8 ; .456/ 3625 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B ) ADDITION ; SOUSTRACTION ;
MULTIPLICATION ; DIVISION de DEUX
FRACTIONS DE DENOMINATEURS DIFFERENTS. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B) Série 1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5 .ADDITION : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculer : |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
; donner
le résultat sous forme irréductible et
sous forme décimale à 0,001 prés . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6. SOUSTRACTION: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculer |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
; donner
le résultat sous forme irréductible et
sous forme décimale à 0,001 prés . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7.MULTIPLICATION |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculer |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
; donner
le résultat sous forme irréductible et
sous forme décimale à 0,001 prés . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8. DIVISION |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculer |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
; donner le résultat sous
forme irréductible et puis sous forme décimale à 0,001 prés . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
B) Série 2 |
|
|
|
Addition |
|
|
|
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la
leçon sur les nombres relatifs |
|
|
|
|
|
|
|
Soustraction |
|
|
|
|
|
|
|
Multiplication |
|
|
|
|
|
|
|
Fraction de fractions |
|
|
|
|
|
|
|
Division de fractions |
|
|
|
|
|
|