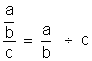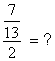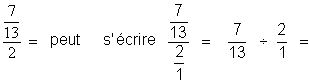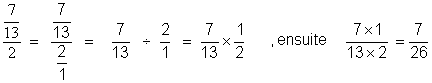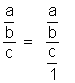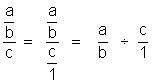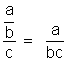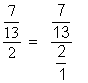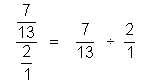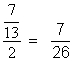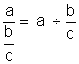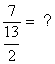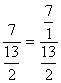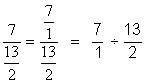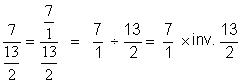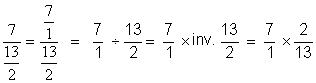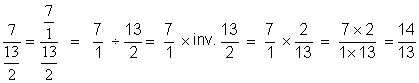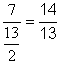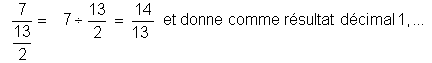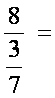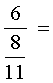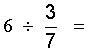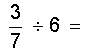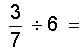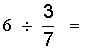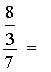Auteur : WARME R.

NOM : ………………………………

Prénom : …………………………..

Classe :…………………..

Année    scolaire : ………………………                                        

Dossier pris le : ……/………/………

Validation de la  formation :    O -  N

 Le : ……………………………………..

Nom du  formateur  : ……………………

ETABLISSEMENT : …………………………………………..

DOC. Info : Professeur ; Formateur

5 - E - Fractions

/ 26

DOC : livre  Elève .Cours  interactifs - et travaux +  corrigés.

TITRE : La  FRACTION    et   un nombre  (DIVISION )

DOSSIER  N°5  ;  INTERACTIF ;LES FRACTIONS (Opérations)

Informations :« TRAVAUX   d’auto - formation » ;Cliquer sur  le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU :

Formation  Niveau V  (inclus le CAP et CFA).

OBJECTIFS :

- Savoir faire des calculs avec une fraction et un  nombre  :. « division ».

D -   Division d ‘une fractions  et d’un nombre .



2 cas à connaître



IV)   INFORMATIONS  «  formation leçon » :

Test

COURS 

Travaux  auto - formation.

1°)Activités précédentes.(problèmes)

Corrigé des travaux  auto - formation.

Contrôle

Evaluation :

2°)INTERDISCIPLINARITE : voir cas par cas ! !

CORRIGE contrôle

CORRIGE  évaluation

Travaux niveau VI et V : en relation avec l’objectif.

Dossier 158 : prendre une fraction d’un nombre.

Dossier 159 : calcul d’un nombre dont on connaît une fraction.

Cette leçon est découpée en trois chapitres distincts . Elle est longue à traiter , tous les calculs élémentaires (bases)  sont a connaître et maîtriser .

Il faut  compter  en moyenne 2 mois  d’études :  à raison  de :

-          15 jours par chapitre , travail  qui doit être  conclu par un devoir ponctuel  sur les règles et calculs élémentaires ; ( soit 1mois et demi )

-          les 15 derniers jours sont réservés au travail de synthèse : chaînes d’opérations avec 3 et plus fractions.

-          Le tout est suivi par un devoir sommatif et des applications interdisciplinaires .

Liste de tests et devoirs à traiter dans l’ordre ..

Ÿ

Série 2 (minimum formation)

 Devoir diagnostique L tests.

Ÿ

 Devoir  Auto  - Formatif  ( intégré au cours)

Ÿ

  Devoir Formatif  « Contrôle : savoir » ;   ( remédiation)

Ÿ

 Devoir  Formatif  «  Evaluation  1 savoir faire »  ( remédiation)

Ÿ

Devoir  Formatif  «  Evaluation  2 savoir faire »  ( remédiation)

Devoir sommatif N°1

Devoir sommatif .N°2

Ÿ

Devoir certificatif : ( remédiation )

Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon

PREAMBULE

N°5 - E

DIVISION d’une FRACTION par un nombre et vice versa  

i9  

DIVISION d’une FRACTION par un nombre et vice versa  ou  d’ un nombre par une fraction .

Cd³ 1 INFO +

Cd³ 2 INFO +

Cd³ 3 INFO +

Attention: on ne doit pas confondre:

 ; qui est « diviser » une fraction par un nombre   ( 1° cas)

                                 et

  qui est «diviser » un nombre  par une fraction »    (2° cas)      

i remarquer  que ce qui  les différencie  est  la position du signe « égal » devant l ‘ une  ou l’autre  des deux barres de  fraction.

Cas 1 : on doit   « Diviser » une fraction par un nombre( entier) »      

Cas 1 :       nous prendrons l’exemple :  :    

Exemple : Cas 1 :    

On transforme l’écriture : «  d’une fraction  par un nombre »   par  « une fraction de « fractions » » ou  la  « division d’une fraction par une fraction »  .

On se souvient que pour diviser deux fractions entre elles il suffit de multiplier la première fraction ( celle du dessus) par l’inverse de la seconde.

      ; »  0,269   ( résultat sous forme décimale à 0,001 près )

Généralisation :

1°) on transforme la fraction divisée par un nombre par la fractions de deux fractions ( la deuxième ayant un dénominateur égal à « 1 »)

2°) on transforme la fraction de fractions en divisions de deux fractions.

3°) On transforme la division en « multiplication de la première fraction par l’inverse de la seconde.

4°) On effectue la multiplication de deux fractions .

5°) rendre compte.                    

Reprise de l’exemple :

1°) Première transformation

2°) Deuxième transformation

Transformer « le nombre  "2" » en fraction de numérateur égal à 1.    

3°) Troisième transformation : seconde. »

« On multiplie la première fraction par l ‘inverse de la seconde fraction ! »

4°) Calcul :  appliquer la règle concernant la multiplication de deux fractions.

5°)  rendre compte :         ;       ou          »  0,269   ( résultat sous forme décimale à 0,001 près )

Cas 2 : on doit   « Diviser » un nombre par  une fraction

cas 2 :          exemple :  

Pour obtenir un résultat ,on opèrera par transformations   successives

On pose « 7 » =   et l’on  remplace   «7 » par la fraction « 7 /1 » :

Nous nous trouvons en présence  d’une fraction de fractions ; que nous transformons en  division de deux fractions

:

Nous remplaçons  la division  de deux fractions par la multiplication de la première par l’inverse de la seconde :

:        ,

Nous savons que l’inverse de 13 /2 est 2/13 ; nous opérons une autre transformation :

       ,

Nous effectuons la multiplication des deux fractions :

Il nous reste à « rendre compte » :

     qui est la  forme irréductible du résultat .

  ou l’on peut calculer « 14 / 13 » et  donner une forme décimale arrondie :

                               1,077 est le résultat arrondi à 0,001 près .

En conclusion :  il faudra faire très attention à la position du signe «  = » ; on peut en effet

ion peut constater que les deux cas donnent des résultats différents ,il est donc trés important de vérifier la position du signe « égal »

alors que :

+Faire les exercices suivants :  

Fraction de fractions

Division de fractions

Leçon

Titre

N°5 E

TRAVAUX d ’ AUTO - FORMATION sur

La division d’une  FRACTION et un nombre ( OPERATIONS )

TRAVAUX  N°5 E  d ’ AUTO - FORMATION :  CONTROLE

Définitions préalables

1°)  Donner la définition d’un fraction : donner un exemple avec 3 et 4

. Exemples ?:

2°)  Qu’est ce qu’un rationnel ?

.

Donner des exemples :

16 : 2 = ?    ………………………………………………

25: 4  =   ?    ………………………………………………

11 : 7  =   ?  …………………………………………………

3°) qu’appelle - t  - on  «  écriture fractionnaire » 

DIVISION d’ UNE FRACTION et d’UN NOMBRE .

Cd³ INFO +

cas  1 : « diviser une fraction par un nombre « c » .

1°) Donner la procédure permettant d’ obtenir  le résultat de la division d’une fraction par un nombre :         

cas 2 :   Division d’un nombre "a"   entier  par une fraction.

 Donner la procédure permettant d ‘obtenir  le résultat de la division d’un nombre  par une fraction :         

TRAVAUX  N°5 E   d ’ AUTO - FORMATION :  EVALUATION

 série 1

Cd³ INFO +

Division d ‘une  fraction par un nombre 

Division d ‘un nombre    par une fraction

Série 2

1°)  Calculer   et  donner le résultat sous  forme d’une fraction simplifiée ; puis sous la forme décimale à 0,001  prés.

a) 

b)

2°)  Calculer   et  donner le résultat sous  forme d’une fraction simplifiée ; puis sous la forme décimale à 0,001  prés

a)

b)