|
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : 1°) Calcul
du a% |
Objectif suivant : Lecture: Indice de vie économique |
DOSSIER : Les
indices simples : Appelés :
" indice simple
" , ou "indice analytique" , ou
"indice élémentaire" , "indice particulier :
Ij/o = 
100
|
TEST |
COURS |
L'indice
simple est un nombre sans unité qui traduit l'évolution dans le temps d'une
grandeur mesurable.
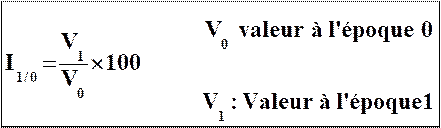
La base de
l'indice est 100 : c'est l'indice de l'époque 0
Si I1/0
> 100, il y a une augmentation entre les époques 0 et 1
Si I1/0
< 100, il y a une diminution entre les époques 0 et 1.
Exemple :
Le prix du faux-filet
était de 21,95 F le Kg en 1970 année de référence, et de 135 F le Kg en 1995,
année de comparaison.
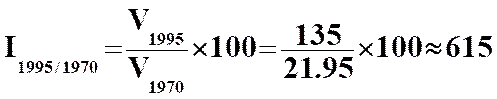
On dit que l'indice simple du
faux-filet en 1995 est de 615 sur la base 100 en 1970
La notion d'indices statistiques apparaît chaque fois que l'on
doit comparer deux grandeurs dans l'espace ou dans le temps à travers leur rapport.
L’indice : l’indice est un nombre
(supérieur à 0 ) qui a pour but de traduire de
l’évolution dans le temps d’une grandeur mesurable :
" évolution des prix , de la bourse , d’une production , de l’évolution en
terme d’emplois (indice du chômage)"
.
Exemple : une
entreprise a payé à l'époque to une matière première "x" , 30 € le
kg; trois ans plus tard ( en t 3 ) elle la paye 36 € le
kg.
Ces
deux prix peuvent être comparés selon trois procédés:
a ) soit en faisant leur différence . En trois ans, le prix de la matière première
"x" a augmenté en valeur absolue
de 36 € - 30 € = 6 € le kg. On notera
que ce procédé ne donne qu'une information imparfaite sur cette
augmentation. En effet, elle ne tient pas compte de l'importance du prix à l'instant to . En d'autres termes, nous aurions eu
le même résultat avec des prix différents, par exemple 23 € et 29 € le kg .
b) soit en estimant l'accroissement de
prix en valeur relative :
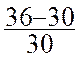= 0,2
ou 0,2 fois 100 = 20 %
c) soit
en faisant le rapport suivant : donnant un "Indice" :
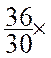100
= 120
Nous avons pris comme base de calcul le
nombre "100" ; par convention, nous prendrons une base "100" pour les calculs
d'indices.
Ce rapport « 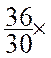100 »
soit « 120 » est
appelé " indice simple " , ou
"indice analytique" , ou "indice élémentaire" ,
"indice particulier".
Généralité : on appelle "indice
simple" d'un phénomène mesurable le rapport des valeurs
Vj
et Vo prises par le
phénomène aux temps "j"
(époque ou année courante) et "O"
(époque ou
année de base )
Ij/o = 100
Remarques :
1°) la variable est ici
"chronologique" ( le temps) . Elle peut , dans d'autres cas
, être spatiale et prendre en compte le changement de lieu.
2°)On
retiendra que le taux d'accroissement est égal à l'indice moins la base ( 100)
et qu'il s'exprime en pourcentage .
Activité 2 : Exemple d’
établissement d’un indice :
Enoncé :
A une date donnée ( t1),
un objet était vendu 3020 €.
Un objet de même type vaut 2490 €. 8
ans plus tard (t2) .Donner l'indice d'évolution du prix ( diminution ou augmentation)
Analyse :
L’objet est vendu moins cher !
On ne cherche pas la valeur de
diminution !
Si l’on fait la division du prix payé 2490 €. en t2
par 3020 €. en t1 on trouve un
nombre :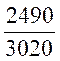 
»
0,8245
Ce nombre de « 0,8245 » s’ appelle
« coefficient multiplicateur » associé à la « diminution » .
La diminution est de 1 – 0,8245 =
0,1755
Cette diminution peut s ‘exprimer
en pourcentage .
Pour ce faire on multipliera le nombre par 100.;
ainsi le taux de diminution est de 0,1755
100 = 17,55 ; soit
17,55 %
Un bien valant 100 €
. , subissant la même variation , vaudrait
82,45 € . 8 ans plus tard.
Le nombre « 82,45 »
représente l’indice du prix de l’objet
(ou du bien) au temps t2 ,
(8 ans plus tard) , si l’on prend 100
pour indice du prix au temps t1 .
Et 17,55 % le taux de diminution du prix de l'objet depuis le date t1 .
L’indice
simple :
L’indice simple traduit l’évolution
dans le temps d’une grandeur mesurable. Il n’ a
pas d’unité .
Attention l'indice simple
ne s’exprime pas en « a% »!!!!
Si l’on appelle « V0 »
la valeur d’une grandeur à l’époque t0
Si l’on appelle « V1 »
la valeur d’une grandeur à l’époque t1
L’indice de la grandeur à l’ époque t1 par rapport à l’époque t0
est un nombre ,sans unité ,tel
que :
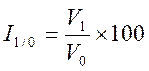
Commentaire :
Si
I1/0 > 100 il y a une augmentation entre les époques t0
et t1.
Si I1/0
< 100 il y a une diminution entre les époques t0 et t1.
Les indices simples ,
que nous venons de définir , ne prennent en compte que la variation d'une seule
composante d'un phénomène . ( exemple le prix du litre
d'essence) . Or il est très rare qu'une
composante explique , à elle seule ,
l'évolution d'un phénomène économique complexe : ( par exemple l'évolution du
prix du baril de pétrole , n'est pas
seulement la conséquence de la variation du prix du litre de super , mais aussi celle des variations de prix
d'autres produits et services ) Il faut donc disposer d'outils
statistiques permettant de tenir compte
de plusieurs composantes .
On fera appelle aux indices synthétiques , ces indices répondent permettent de tenir
compte de plusieurs composantes , en
combinant l'évolution simultanée de plusieurs phénomènes , chacun d'eux étant
mesuré par un indice simple .
( cliquer ici pour info plus !!!! sur les indices
synthétiques )
Activité : On donne le tableau
sur les indices du coût de la construction .Il permet de calculer les
augmentations de loyer pour de nombreux appartements . La base "100" est le quatrième trimestre
1953 .
Remarque :L'indice et le prix de ce
produit sont des grandeurs proportionnelles:
( pour faire une transformation puis calculs il faut connaître trois valeurs
sur quatre)
D'où le tableau :
|
|
Année 1953 |
Année
1997 |
|
Indice |
100 |
1068 |
|
Prix |
"x" |
1068
€ |
D'où
"x" = 100 €
|
|
Année |
Indice
4e trimestre |
|
Un loyer qui était de 1068 € en
1997 était de 100 €. On remarque qu'en 1995 l'indice de la construction a baissé . |
1986 |
881 |
|
1987 |
890 |
|
|
1988 |
919 |
|
|
1989 |
927 |
|
|
1990 |
952 |
|
|
1991 |
1002 |
|
|
1992 |
1005 |
|
|
1993 |
1016 |
|
|
1994 |
1019 |
|
|
1995 |
1013 |
|
|
1996 |
1046 |
|
|
1997 |
1068 |
Activité 2 : Le loyer d'un atelier était de 2814 € en 1992 pour un indice de 1005.
Question : On cherche le montant du loyer en 1997
, l'indice étant de 1068.
On complète le tableau de proportionnalité
:
|
|
Année 1992 |
Année
1997 |
|
Indice |
1005 |
1068 |
|
Prix |
2
814 € |
"x" |
On sort
la proportion :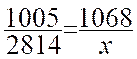 
; on transforme
"x" =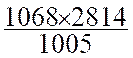 
"x" = 2990,40 €
Activité 3:
En 1998 , le
prix d'un poste de télévision était 3200
€ . Le prix en 2001 est de 3328 € . En prenant pour
base 100 l'année 1998 , chercher l'indice du prix en
2001.
On complète le tableau de
proportionnalité :
|
|
Année 1998 |
Année
2001 |
|
Indice |
100 |
"x" |
|
Prix |
3200
€ |
3328
€ |
On sort
la proportion :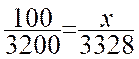 
; on transforme
"x" =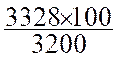 
"x" = 104 ; l'indice est de 104
CONTROLE :
1°) Qu'est ce
qu'un indice ?
2°) Qu' est ce qu'un indice simple
?
3°)
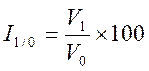: que signifie cette formule ?
On
donne la formule suivante :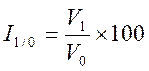
1°) Le
prix du litre d'essence était à l'époque
to de 1,75 €; il est de 2,35 € à l'époque tn .Quelle est l'évolution du prix de l'essence ( en
indice) ?
2°) A
une date donnée ( t1), un objet était vendu
3020 €.
Un
objet de même type vaut 2490 €. 8 ans plus tard (t2) .Donner
l'indice d'évolution du prix (s’agit t- il
d’une diminution ou
augmentation ?).
3°) une entreprise a payé à
l'époque to une matière première "x" , 30 € le kg;
trois ans plus tard ( en t 3
) elle la paye 36 € le kg. Quel est
l'indice d'évolution ? que est le taux de cette évolution ?
4°) Le loyer d'un atelier
était de 2814 € en 1992 pour un
indice de 1005.
Question : On cherche le montant du loyer en 1997
, l'indice étant de 1068.
5°) En 1998 ,
le prix d'un poste de télévision était
3200 € . Le prix en 2001 est de
3328 € .
En prenant pour base 100 l'année 1998 , chercher
l'indice du prix en 2001.