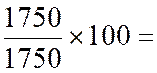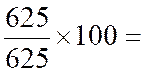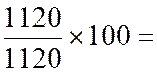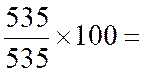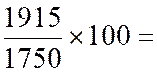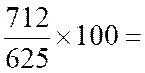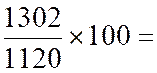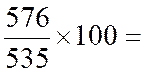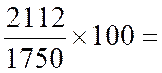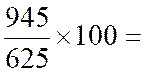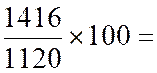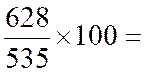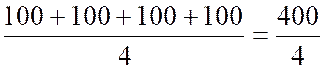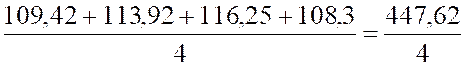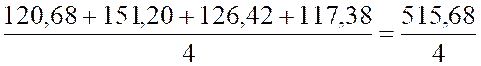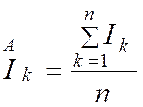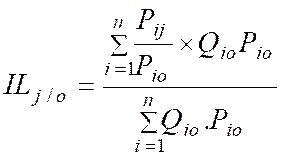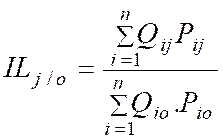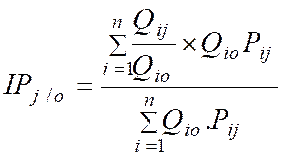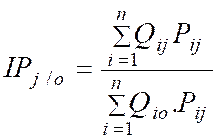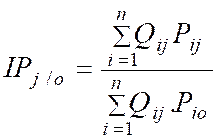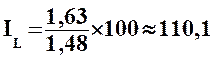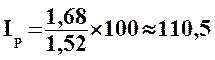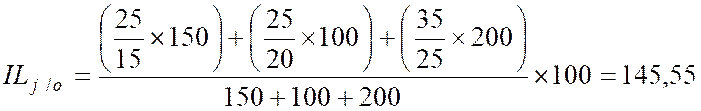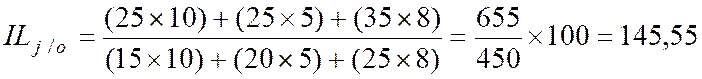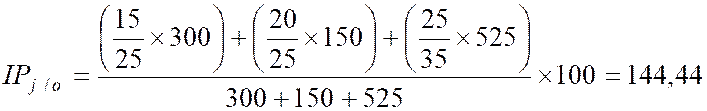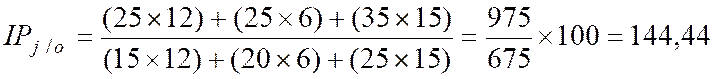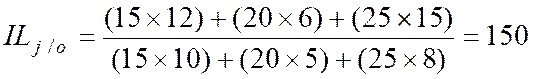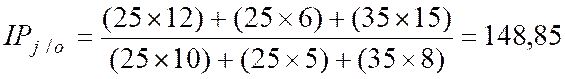ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant |
DOSSIER : Les indices composés ou
synthétiques.
1. Notion d'indice synthétique:
2. Choix de la moyenne utilisée ;
3. Résumé
sur les indices de la vie économique :
Le problème
que pose la pondération ;L’indice des prix :
·
La méthode de Laspeyres
·
La méthode de Paasche
· Etude 1
et 2 d'un exemple appliquant les deux
méthodes.
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
1°)
Notion d'indice synthétique:
Les indices simples ,
que nous avons défini , ne prennent en compte que la variation d'une seule
composante d'un phénomène . ( exemple le prix du litre
d'essence) . Or il est très rare qu'une
composante explique , à elle seule ,
l'évolution d'un phénomène économique complexe : ( par exemple l'évolution du
prix du baril de pétrole , n'est pas
seulement la conséquence de la variation du prix du litre de super , mais aussi celle des variations de prix
d'autres produits et services ) Il faut donc disposer d'outils statistiques permettant de tenir compte de plusieurs
composantes .
On fera appelle aux indices synthétiques , ces indices répondent permettent de tenir
compte de plusieurs composantes , en
combinant l'évolution simultanée de plusieurs phénomènes , chacun d'eux étant mesuré
par un indice simple .
Cette procédure (
synthétique) pose différents problèmes:
-
celui du choix de la moyenne utilisée ;
-
celui de la pondération , c'est à dire de la
"charge" (ou coefficient) relative de chaque composante dans l'ensemble .
Exemple : une entreprise dispose , au
cours du premier trimestre de l'époque t3 d'un stock de produits
répartis en quatre catégories A , B , C , D , dont les quantités exprimées en
tonnes , sont les suivantes :
|
Mois |
Catégorie
A |
Catégorie
B |
Catégorie
C |
Catégorie
D |
|
Janvier Février Mars |
1780 1975 2146 |
654 745 962 |
1120 1380 1456 |
542 586 634 |
Il faut effectuer le calcul des indices
simples par catégories de produits , puis en faire une moyenne.
2°)
Choix de la moyenne utilisée :
Exemple :
Soit une entreprise : une entreprise dispose , au cours du
premier trimestre de l'époque t3 d'un stock de tablettes
tactile répartis en quatre catégories A
, B , C , D , dont les quantités exprimées « millier » , sont les
suivantes :
|
Mois |
Catégorie
A |
Catégorie
B |
Catégorie
C |
Catégorie
D |
|
Janvier Février Mars |
1750 1915 2112
|
625 712 945 |
1120 1302 1416 |
535 576 628 |
Il semble logique de retenir comme
indice synthétique la moyenne arithmétique des indices simples des éléments qui
composent l'indice .
|
|
Mois |
Indice de la catégorie « A » |
Indice de la catégorie « B » |
Indice de la catégorie « C » |
Indice de la catégorie « D » |
|
|
|
Janvier |
|
|
|
|
|
|
|
Février |
|
|
|
|
|
|
|
Mars |
|
|
|
|
|
Le mois de
janvier est choisi comme base = 100 .
|
|
Déterminons,
mois par mois, la moyenne des indices. |
|
|
|
Janvier :
|
|
|
|
Février :
|
|
|
|
Mars :
|
|
|
|
Nous
pouvons généraliser
, en considérant « n » indices simples :
Remarque :
il est possible de faire ce type de calcul à partir des autres moyennes . ( exemples : moyenne géométrique , moyenne
harmonique ;..) |
|
|
|
|
|
L'indice
composé
permet d'étudier les prix de plusieurs
grandeurs entre deux périodes (période 0 et période 1).
3°)
Les indices de la vie économique :
Problème
posé par la pondération. Et calculs de
l’indice des prix il existe deux méthodes de calculs .
a) La
méthode de Laspeyres :
On sélectionne plusieurs articles et on calcule leurs prix en
fonction des quantités de référence à l'époque 0. Puis on calcule les prix de
ces articles pour les mêmes quantités qu'à l'époque 0 pour l'époque 1.
On fait
ensuite la somme des prix pour l'époque 0 et la somme des prix pour l'époque 1.
On calcule
ensuite l'indice de Laspeyres IL (Indice de base 100) de la façon
suivante :
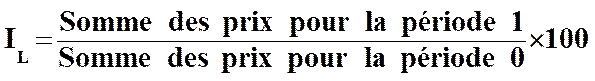
autrement :
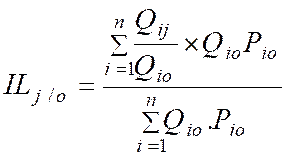 (1)
(1)
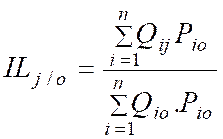 (2)
(2)
|
l'indice de Laspeyres IL |
Indice
des quantités. |
|
Indice
des prix. |
|
|
|
|
|
|
|
|
Formule simplifiée |
(2) |
Formule simplifiée |
|
|
C'est avec cette
méthode que l'INSEE calcule l'indice de la consommation des ménages (hors
tabac).
b °) La
méthode de Paasche :
Le principe
est exactement le même que la méthode précédente, sauf qu'ici on prend les
quantités de l'époque 1 comme référence.
|
l'indice de Paasche IP |
Indice
des quantités. |
|
Indice
des prix. |
|
|
|
|
|
|
|
|
Formule simplifiée |
(3) |
|
|
|