|
23 / 26. |
DOC : livre Elève
.Cours interactifs - et travaux + corrigés. |
FL3
:
|
DOSSIER N°23 |
Information « TRAVAUX d’auto - formation » |
|
05/06 NIVEAU : Formation Niveau V |
OBJECTIFS : - Savoir reconnaître l’équation, la représentation graphique , une
fonction linéaire. - Savoir reconnaître le tableau de proportionnalité représentant la
fonction linéaire. |
I
)
Pré requis:
|
¥ |
|
|
INFO : Les différentes représentations graphiques de fonctions. |
¥ |
|
¥ |
|
II
)
ENVIRONNEMENT du dossier :
|
Objectif
précédent : |
Objectif
suivant : |
Complément
de lecture : 1°)Les
fonctions : |
|
|
|
|
|
|
III )
LECON n° 23 :
Ses modèles
de représentation mathématique ; passage d’un modèle à l’autre
CHAPITRES
:
IV)
INFORMATIONS « formation
leçon » :
|
|
Travaux auto - formation. |
Corrigé
des travaux auto - formation. |
||||
|
Contrôle |
évaluation |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*
remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour
conclure une formation .
|
Titre |
|
|
N°23 |
Ses modèles de représentation
mathématique ; passage d’un modèle à l’autre |
CHAPITRES
:
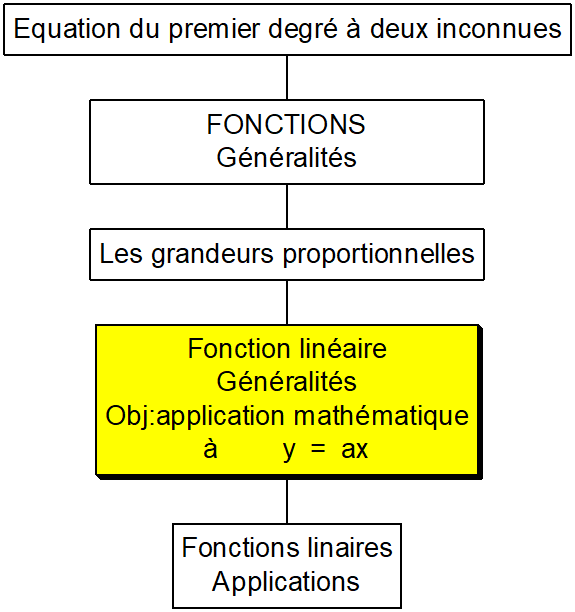
Il faut traiter dans l’ordre :
|
MODELES
MATHEMATIQUES de représentation
de la fonction linéaire |
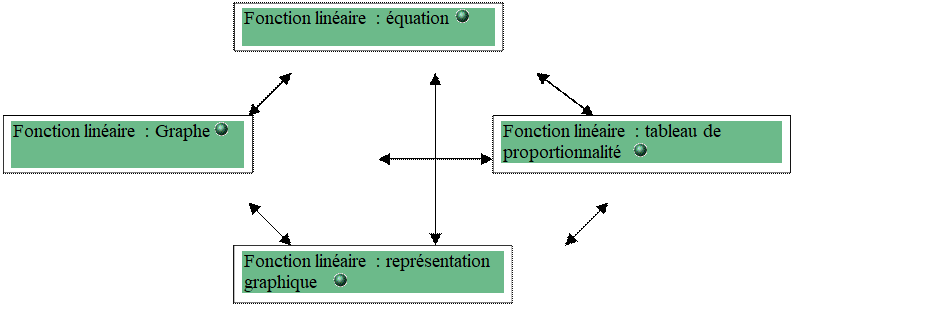
cet objectif traite des généralités sur la fonction linéaire :
Une
fonction linéaire peut s’identifier à partir de quatre modes de représentation :
I ) Equation
II ) Graphe
III )
Tableau de variation (de proportionnalité)
I V ) Représentation graphique.
Dans ce cours nous prenons
l’équation:
y = 
x est pris
comme exemple.
(elle est de la forme « y = a x
» ; dans l’exemple
« a » = ; » 0, 67 )
Les
transformations possibles :
|
|
Equation
|
Graphe
|
Tableau
|
Représentation graphique
|
Equation
|
|
|
|
|
Graphe
|
|
|
|
|
Tableau
|
|
|
|
|
Représentation graphique
|
|
|
|
|
On peut obtenir une équation
à partir : d’un graphe ; d’un tableau de
proportionnalité ; d’une représentation graphique.
L’ équation de la fonction linéaire est de la forme y = ax
La notation mathématique de la fonction
linéaire f : x
ax
traduction
en langage littérale : « fonction » où « x » a pour image « a » fois « x ».
Ce
que signifie : « a
x »
« a » est un nombre
donné, (bien entendu différent de zéro ; dans ce cas la fonction linéaire
n’existerait pas pour « 0 » multiplié par « x » égal
« 0 » ) ;
«a» est appelé « coefficient directeur » dans la
représentation graphique .
« x » est la variable de la fonction.
Exemple :
y = x est une équation d’une fonction linéaire
parce qu’elle est de la forme y = ax
la
fonction se notera f : xx
traduction
en langage littérale : « fonction » où « x » a pour image « » fois « x ».
Ce
que signifie : « x »
«»
est appelé « coefficient directeur »
dans la représentation graphique . « x »
est la variable de la fonction.
On dira :
La
fonction linéaire de coefficient « »
fait correspondre à chaque valeur de la variable « x » le nombre
« x ».
L’équation représentant de la fonction
linéaire est une équation du premier
degré à deux inconnues de la forme y = x
Plus
généralement : (on dira que J
L’équation représentant de la fonction
linéaire est une équation du premier
degré à deux inconnues de la forme y = a
x ; « a » étant le coefficient de l’équation de la fonction
linéaire
Le rapport
de « y » sur « x »
est , pour la fonction linéaire, égal au rapport « x »
sur « x » ;
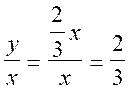
Dans la fonction linéaire ce nombre est constant il
est égal à «»
Ce nombre «»
est appelé « coefficient de proportionnalité » ;
Le tableau s’appellera « tableau de
proportionnalité ».
A ) Obtention d’ une équation à partir
d’un graphe
CALCUL DE « a » à partir d’un couple de nombres représentant une fonction
linéaire :
En vue d’obtenir une équation de
la forme y = ax
On analyse le
graphe : G = {( 0 ; 0) ; (3 ;2) ; (9 ; 6 ) }
On reconnaît que la droite passe
par zéro .on peut dire le troisième couple de nombres (9 ; 6
) est de la forme (x ; ax) ;
Nous pouvons en déduire que le graphe représentant une fonction linéaire
est d’équation y = ax .
;le nombre « 9 » est la valeur de
« x » ;le nombre « 6 » est la valeur de
« y » ;nous remplaçons ces valeurs dans l’équation ( y =ax devient
6 = a 
9 , nous en déduisons que a =
, après simplification a =
nous concluons : le graphe G = {(
0 ; 0) ; (3 ;2) ; (9 ; 6 ) } donne l’équation de
la fonction linéaire y = x
B ) Obtention d’ une équation à partir
d’un tableau de proportionnalité
On nous donne le tableau suivant :
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
On
nous déclare que le tableau est un tableau de proportionnalité !
On sait qu’en faisant le calcul du rapport 
on trouve une valeur à « a »
Ainsi on prend un point ( E ) on identifie
x = 2 et y = 6
On fait le calcul : 
= a
= 3
Donc si « a » = 3; l’équation de la
fonction linéaire représentant le tableau sera
y = 3x
Vérification : les couples de nombres forment une suite de rapports ; ils faut
vérifier si ils forment une suite de nombres proportionnels ou une
suite
de rapports égaux
= ? = 
= ?
= 
= ?=
= ?== ?=
il faut faire les calculs ! ! !
ou
voir la « somme
des rapports égaux »
C ) Obtention d’ une
équation à partir d’une représentation
graphique.
On choisit un point et l’on
relève ses coordonnées : Le point A à
pour abscisse x =+10 ; et pour
ordonnée y = + 5
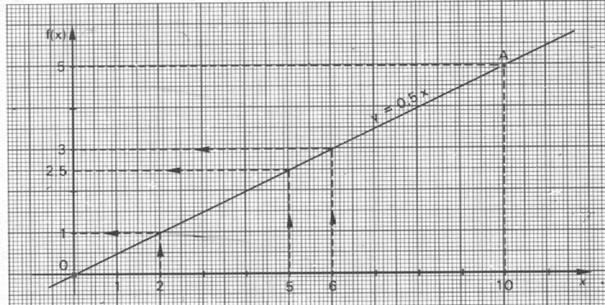
Il
faut faire le rapport de pour
avoir le coefficient « a » :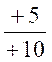 
= 0,5
Conclusion : la droite à pour
équation y = 0,5 x
|
II )
GRAPHE de la fonction linéaire |
On peut obtenir un graphe à partir : d’une équation ; d’un
tableau de proportionnalité ; d’une représentation graphique.
Le graphe est un ensemble (ou suite)
de couples de nombres ;du type : ( x ; ax)
le premier nombre est
attribué à « x » appelé « variable »
le deuxième nombre est associer
au produit « ax ».
Si « a » vaut ,le
couple aura la forme et sera
noté :( x ; x)
le
Graphe de la fonction linéaire se présentera sous la forme :
G = { ( x1 ; ax1) ;
(x2 ;ax2 ) ; ......... }
A ) Construction d’un graphe à partir de l’équation : y = x
Obtention
d’un couple de nombres (à partir
d’une équation) :
On donne une valeur à « x »
(exemple : 9 )
on
obtient un autre nombre en utilisant
l’équation y = x ; (y = 9
=(18 :3 ) = 6)
en résumé : si
« x » = 9 alors x
= 6
nous
obtenons le premier couple de nombres du graphe de la fonction « x » : (9 ; 6)
On remarque que l’on peut citer
un couple particulier : (0 ;0) ( en effet si « x » = 0 alors x
Nous
obtenons un premier modèle mathématique de la forme :
G
= { ( 0 ; 0 ) ; ( x1 ;
x1) ;
(x2 ; x2
) ; ......... }
le couple (x1 ; x1) dans un repère cartésien signifie :
qu’ à x1 on
associe l’abscisse « x »
qu’ à « x1 »
on associe l’ordonnée « y1 »
En modèle « limité » nous
pouvons utiliser le graphe suivant :
le graphe représentant l ’ équation y = x est G = {( 0 ; 0) ; ( 3 ; 2
) ;(9 ; 6 ) ; }
deux points suffissent , le troisième point servira pour vérifier si
le tracé est « bon »
soit le graphe obtenu précédemment G = {( 0 ;
0) ; (9 ; 6 )}
ces
deux couples de nombres permettent de tracer la représentation graphique de la fonction .
B) Obtention d’un graphe à partir d’une représentation graphique .
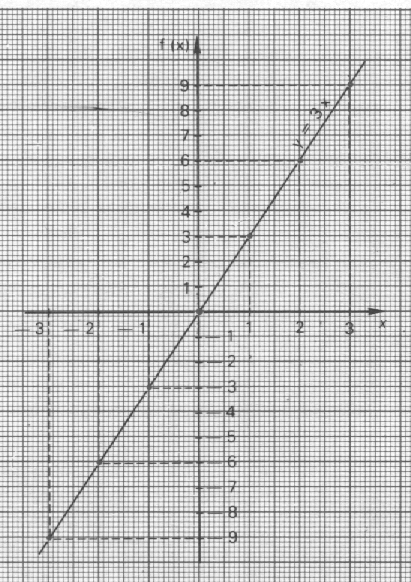
G = { ( -3 ; -9) ; (-2 ;-6 ) ;
(-1 ;-3 ) ; ( 0 ; 0 ) ;
(1 ; 3 ) ; (2 ;6 ) ; ( 3 ;9
) ; ......... }
C) Obtention d’un graphe à partir d’un tableau de variation
On nous donne le tableau suivant :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
Pour construire le graphe il suffit de reprendre
les couples de nombres dans l’ordre
croissant de « x » ; ce qui donne le graphe :
G = { ( -3 ; -9) ; (-2 ;-6 ) ;
(-1 ;-3 ) ; ( 0 ; 0 ) ;
(1 ; 3 ) ; (2 ;6 ) ; ( 3 ;9 ) }
Plus
généralement on dira :
que le Graphe de la fonction linéaire est de la forme :
G = {( 0 ; 0 ) ; ( 0 ; 1
) ; ( x1 ; ax1) ; (x2 ;ax2
) ; ......... }
Ce graphe est « fini » si il est obtenu à partir d’un
tableau ; il est « infini »
si il est obtenu à partir d’une équation ou d’une représentation graphique.
Avec comme les deux couples
particuliers :
( 0 ; 0 ) et ( 1 ; a )
|
III) TABLEAU de variation dit « tableau de
proportionnalité » |
(regroupant les couples ( x ; ax) )
On
peut obtenir un tableau de proportionnalité à partir d’ un graphe:
d’une équation ;; d’une représentation graphique.
Voir Fonction généralité « tableau de variation » :
A ) On
peut obtenir un tableau de proportionnalité à partir d’ un graphe
Soit le
graphe :
G = { ( -3 ;
-9) ; (-2 ;-6 ) ; (-1 ;-3 ) ; ( 0 ; 0
) ; (1 ; 3 ) ; (2
;6 ) ; ( 3 ;9 ) ; ......... }
On
place les couples de nombres dans le tableau suivant :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Le
tableau de variation sera :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
B) On peut
obtenir un tableau de proportionnalité à partir d’une équation.
Soit
l’équation y = 3x
1°
)On trace le tableau :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
2°)
on choisit des valeurs pour « x »
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
a x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
|
|
|
|
|
|
|
3°)
on donne la valeur à « a » , et l’on effectue tous les calculs pour
trouver « y ».
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y = 3x |
3 |
3 -6 |
3 -3 |
3 0 |
3 3 |
3 6 |
3 9 |
Conclusion :
Le
tableau de proportionnalité représentant la fonction : y = 3x est :
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
Remarque :
le tableau peut se réduire à 3 colonnes de valeurs : ( suffisant pour
tracer une droite)
|
|
|
A |
B |
C |
O |
D |
E |
F |
|
3 x |
x |
|
-2 |
|
0 |
1 |
|
|
|
|
y |
|
-6 |
|
0 |
3 |
|
|
C ) On peut obtenir
un tableau de proportionnalité à partir d’une représentation
graphique.
Sur la droite on place des points que l’on
nomme : A ;B ; C ; O ;D ;E ;F Le
nombre de points est défini à partir de contraintes imposées ! !
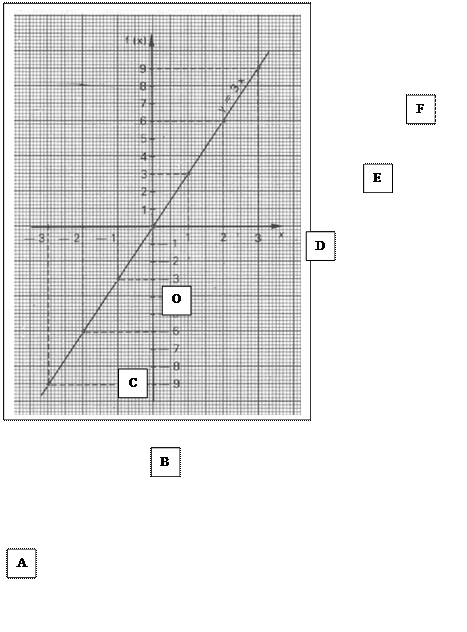
On
trace le tableau :
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Le tableau est « rempli » à partir des
résultats trouvés sur la droite :
Pour chaque point on relève son
abscisse et son ordonnée
|
|
A |
B |
C |
O |
D |
E |
F |
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
-9 |
-6 |
-3 |
0 |
3 |
6 |
9 |
Les coordonnées du point A peuvent se noter
verticalement :
A -3 au lieu de A (-3 ; -9 )
-9
A chaque point (A ;B ;.....) est associé les deux nombres qui
serviront de coordonnées
Plus généralement :
Modèle
de tableau de proportionnalité :
|
|
|
A |
O |
|
B |
C |
|
D |
E |
|
|
|
|
relation |
x |
xA |
0 |
1 |
Valeurs choisies
de la variable |
|
||||||
|
« ax » |
y |
yA |
0 |
a |
Valeurs «des « y » obtenues par calcul |
|
||||||
xA
et yA sont
les coordonnées du point A
ces valeurs peuvent se noter verticalement :
A xA ou horizontalement A (xA ,yA)
yA
On
peut obtenir une représentation graphique
à partir d’une équation , d’ un
tableau de proportionnalité ou à partir d’ un graphe.
A ) Obtention d’ une représentation graphique à partir
d’une équation
Soit l’équation
y = 3 x
La
représentation graphique d ’ une équation passe par la recherche de plusieurs couples de nombres ,utilisés
comme coordonnées .
Deux points suffissent pour tracer la droite ;plus
un troisième qui servira de moyen de vérification (il doit se trouver sur cette
droite )
L’ensemble des points A, B ,C ,D, .... ont pour
coordonnés les couples de nombres (x ;
3x ) .
On peut tracer un tableau :
|
|
O |
A |
B |
|
|
0 |
1 |
2 |
|
y |
0 |
3 |
6 |
Tracé :
B A O
B ) Représentation graphique d’une fonction
linéaire à partir d’un graphe :
Soit
G = { (
0 ; 0 ) ; (1 ; 3 ) ;
(2 ;6 ) }
Procédure :
A chaque couple on attribue une lettre
majuscule :
Le premier couple représente les coordonnées du
point « O » : O (
0 ; 0)
Le deuxième couple représente les coordonnées du
point « A » : A (1 ;
3 )
Le troisième couple servira de « vérificateur » si x =
2 ; y = 6
Représentation graphique : voir la représentation graphique précédente.
C ) Représentation
graphique d’une fonction linéaire à
partir d’un tableau :
On donne le tableau suivant :
|
|
O |
D |
E |
|
x |
0 |
+1 |
+3 |
|
y |
0 |
+2/3 |
+2 |
y
|
|
2
1
+
x
1 2 3
Il suffit
de placer les points O ;D ;
E dans le repère cartésien.
Commentaire :
Le coefficient directeur « »
est un nombre relatif .
« »
peut s’appeler :
n Coefficient de
proportionnalité (dans le tableau)
n Coefficient directeur de la droite
de la fonction linéaire.
n Coefficient directeur de la droit
d’équation y = x ;
dans la représentation graphique
Dans un repère cartésien « orthogonal » ;
dans la représentation graphique de l’équation y = x ; «» est appelé « pente de la
droite », la « pente » étant
appelée aussi « tangente » ;
la
pente est obtenu par le rapport de
« y » sur
« x ».
Voir les relations trigonométriques dans un triangle rectangle
Plus généralement :
Les caractéristiques de la représentation
graphique d’une fonction linéaire
sont :
n c’est
une droite (D)
n cette
droite passe par l’origine « O » d ’ abscisse (0) et d’ordonnée
(0) , noté (0 ;0)
n elle
possède un point caractéristique ; à
d’abscisse valeur « 1 »
correspond la valeur de « a » ;
noté P :(1 ; a)
« a»
s’appelle coefficient directeur de la
droite , c’est un nombre relatif :
Remarques :
si « a »
est « positif » ,dans
la représentation graphique la droite monte de la gauche vers la droite ,on
dira que la fonction est « croissante ».
si « a »
est « négatif » ,dans la
représentation graphique la droite descend du haut gauche du repère vers le bas
droite ,on dira que la fonction est « décroissante ».
|
V ) RELATION
entre « a » et la « pente » et « la
tangente » et « coefficient directeur de la droite » |
|
« a » est
aussi appelé « PENTE » et
« TANGENTE »
«»
est aussi appelé
« pente » ou « tangente » de la droite. (voir
relations trigonométriques dans le
triangle rectangle )
A
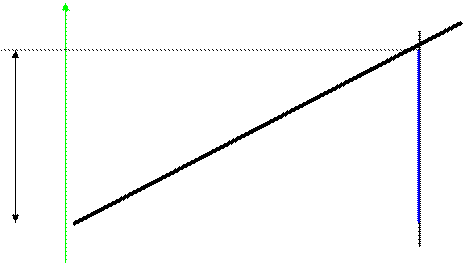
yA
0
·
xA
A’
la pente
est égale au rapport de la longueur « yA »
sur la longueur « xA » (uniquement
vraie si nous sommes dans le sens croissant ) ;
Autrement :
on dit aussi égale au rapport de la mesure algébrique du segment
AA’ sur la mesure algébrique du
segment OA’ ;
on dit aussi
au rapport du coté
opposé a
l’angle (AA’ ) sur le coté adjacent (OA’)
on dit
aussi égale à l’abscisse du point A sur
l’ordonnée du point A
|
Leçon |
Titre |
|
N°23 |
TRAVAUX d ’ AUTO - FORMATION sur |
a)
Quelle condition doit remplir un « tableau numérique » pour
être le représentant d’une fonction ?
b)
Que désigne le mot « variable » ?
1°)
Donnez le modèle mathématique de l’équation
représentant la fonction linéaire.
2°)
Que peut-on représenter à partir d’une
équation représentant la fonction
linéaire ?.
3°)
Soit la notation « ax » , comment nomme - t - on les facteurs ?
4°)
Donnez la forme des couples qui forment eux mêmes le graphe de la fonction linéaire.
5°) Donner forment du graphe de la fonction
linéaire. ( donner les deux couples particuliers)
6°) Représenter le tableau de
« proportionnalité ; précisez ce qu’il « contient ».
7°
) « a » (dans le produit de
facteurs associés à la fonction linéaire) possède trois appellations
, quelles sont - elles ?
8°
) Définissez « la
représentation graphique »
précisez ,en citant les caractéristiques
principales ; placer les dans un repère cartésien.
9° ) Comment
reconnaît - on une fonction dite « linéaire » ?
Soit les fonctions :
|
y1
= 2x |
y2
= - 2x |
y3
= - |
1°) Dans un repère cartésien orthonormé ; Faire
la représentation graphique de chaque fonction .
|
A l' équation y1 = 2x |
On associe la droite D1 (lire :droite indice 1) |
|
A l' équation y2 = - 2x |
On associe la droite D2 (lire :droite
indice 2) |
|
A l' équation y3 = - |
On associe la droite D3 (lire :droite indice 3) |
2°) En
étudiant le graphique , donner les coordonnées du point d’intersection des deux
droites D1 et D2;
3°)
tracer D3
Ensuite : avec un rapporteur donner la valeur de l’angle faite entre les
droites D1 et D3 .
Quel commentaire pouvez-vous avoir sur la position des droites l’une par
rapport à l’autre ?
4° ) Faite
le calcul du produit a1 par a3 .
5°) tracer la droite d'équation y4 = 
mesurer l’angle fait par D2 et D4 ; faire le produit a2 a4
6°)comparer les résultats de la question 4° et 5°;
quelle conclusion peut - on en tirer ?