|
Niveau.
V |
DOSSIER : FONCTIONS LINEAIRES / les grandeurs
proportionnelles / Objectif cours
51 |
|
||
|
|
|
|
||
Pré requis:
|
Arithmétique (problèmes) |
|
Classe 4ème |
ENVIRONNEMENT du dossier:
|
Notions sur
les grandeurs proportionnelles sur les
grandeurs proportionnelles. |
DOSSIER :
Les grandeurs proportionnelles (le coefficient de
proportionnalité) et la fonction linéaire .
|
TEST |
COURS |
|
|||||
|
|
|||||||
|
Résumé
des informations remises ou diffusées
sur la proportionnalité vue au collège. |
|||||||
COURS
Info « Repère » :
|
|
Grandeurs directement
proportionnelles et coefficient de proportionnalité :
En arithmétique on a étudié les grandeurs
directement proportionnelles :
Prix et longueur ; prix et
masse ; prix et litres de carburant , distance
parcourue et temps de parcours , salaire gagné et durée du travail , etc.
Ainsi nous savons que : deux grandeurs sont
directement proportionnelles lorsque les divers valeurs de l’une sont
proportionnelles aux valeurs correspondantes de l’autre .
Ainsi un piéton marchant à la vitesse constante de 6 km à l’heure
parcours en 1 heure : 6 km ; en 2 heures : 12 km ; en 3
heures : 18 km …en 6 heures : 36 km.
On a bien 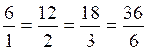 car tous ces
quotients sont égaux à 6.
car tous ces
quotients sont égaux à 6.
Le quotient de deux valeurs
correspondantes des grandeurs considérées est constant .
On l’appelle « coefficient
de proportionnalité » .
Quand on désigne par « x » la mesure du temps et par
« y » la mesure de la
distance parcourue correspondante , le coefficient de
proportionnalité s ‘exprime par le quotient : ![]() = 6 , d’où on déduit
la relation y = 6x
= 6 , d’où on déduit
la relation y = 6x
Plus généralement , « y » et
« x » étant les mesures correspondantes de deux grandeurs
proportionnelles , « a » le coefficient de proportionnalité , ces
mesures sont liées par relation .
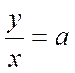 qui s’écrit également y =
a x
qui s’écrit également y =
a x
commentaires :
ces relations s’appliquent non seulement aux nombres arithmétiques
, mais encore aux nombres
algébriques .
Ainsi :
Deux grandeurs sont directement proportionnelles lorsque la mesure de
l’une « y » s’obtient en
multipliant la mesure correspondante de l’autre « x » par un nombre constant « k »,
appelé « coefficient de proportionnalité » :
![]() =
=![]() =
= ![]() =
= ![]() = k
= k
Représentation graphique :
|
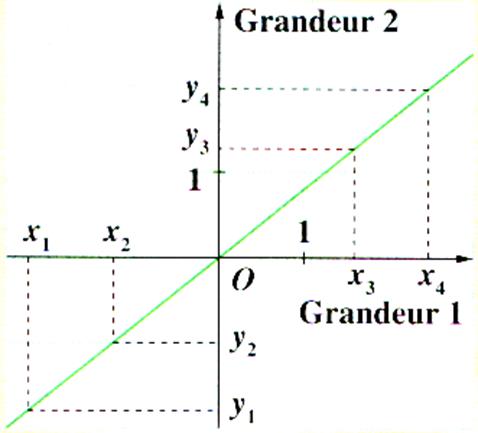
La 1ère grandeur et la 2ème grandeur sont
proportionnelles. |
|
|
![]()
|
1ère
grandeur |
x1 |
x2 |
x3 |
x4 |
|
2ème
grandeur |
y1 |
y2 |
y3 |
y4 |
Attention : le calcul de
rapport se fait toujours « "deuxième grandeur divisée par la première
grandeur » .
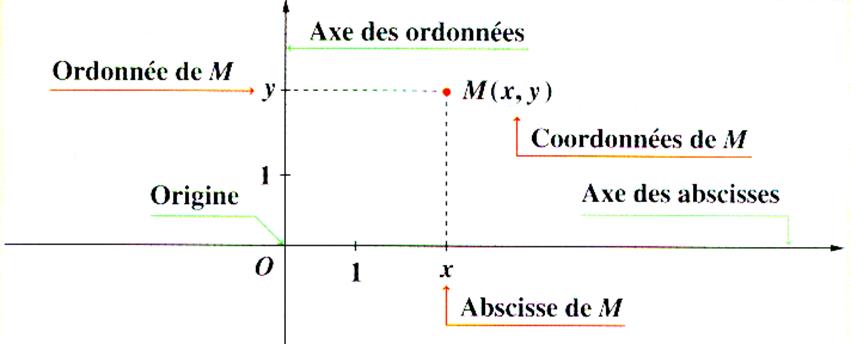
On reconnaît graphiquement que deux
grandeurs sont proportionnelles quand les points de coordonnées ( x ,
y ) sont alignés sur une droite qui passe par l’origine du repère .
|
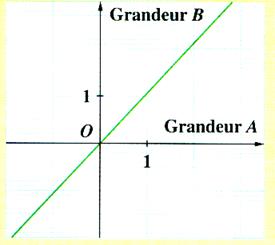
Représentation graphique : Les grandeurs A et B sont proportionnelles |
|
|
|
|
|
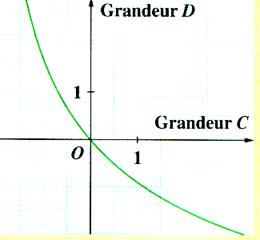
Représentation graphique : Nous sommes en présence d’une courbe . Les grandeurs C et D ne sont pas
proportionnelles |
|
APPLICATION : problème
Un
piéton marche à la vitesse de 6 km à l’heure.
Représenter
graphiquement la distance parcourue .
Solution :
prendre comme unité de temps l’heure et comme unité de longueur le kilomètre.
En
« x » heures , le piéton parcourt une
distance de « y » km égale
à : y = 6 x
La
représentation graphique est une droite de la fonction dite
« linéaire » y = 6x
TRAVAUX AUTO FORMATIFS.
1°) « y » et « x » étant les mesures correspondantes
de deux grandeurs proportionnelles , « a »
le coefficient de proportionnalité , ces mesures sont liées par une relation ; laquelle ? qui s ‘écrit également ?
2°) Quand dit –on que deux
grandeurs sont « directement proportionnelles » ?
1°) Les
deux suites [
9 ;11 ;19 ;25 ;31 ;]
et [27 ;
33 ;57 ;75 ;93 ;] sont - elles des suites
de nombres proportionnelles ?
|
9 |
11 |
19 |
25 |
31 |
|
27 |
33 |
57 |
75 |
93 |
2°) Si l’on paye dans un restaurant 1200 €
pour un mois (30 jours)de pension
,que paiera-t-on pour :
5 jours ; 12jours ; 21 jours
3°)
Calculer la mesure de la d.d.p. aux bornes
d’un résistor
dans les cas suivants :
|
calibre |
Echelle |
lecture |
d.d.p. |
|
3 V |
[ 0 ;
30 [ |
22
divisions |
|
4°)
Quelle est l’intensité du courant traversant le circuit ?
|
Calibre |
Echelle |
lecture |
|
0,1
A |
( 0 ;
100) |
|
5°) Une voiture consomme 18,4 l d’essence pour
effectuer le trajet Paris - Caen ( 230 km) .Quelle sera sa consommation pour effectuer le
trajet Paris - Cherbourg
long de 340 km ?
Que devons nous admettre pour résoudre le problème ?
6°) La
masse et le volume d’un corps sont deux grandeurs directement
proportionnelles .Le coefficient de proportionnalité s’appelle la « masse
volumique » du corps.
Calculer
le volume d’un corps de masse 52 kg dont
la masse
volumique
est de 23 kg /dm3
7° ) De l’égalité 3,4 x 7,8 = 2,4
x 11,05 ; déduire toutes les proportions possibles.
8° ) Calculer x dans chacun des cas suivants :
|
|
|
|
|
|
|
|
|
|
|
|
9°
) Les deux suites [
9 ;11 ;19 ;25 ;31 ;]
et [27 ; 33 ;57 ;75 ;93 ;]
sont - elles des suites de nombres proportionnelles ?
10°) A et B étant des grandeurs directement proportionnelles , compléter le tableau :
|
Mesure de A |
. |
21 |
35 |
|
70 |
280 |
|
|
Mesure de B |
2 |
|
10 |
18 |
|
|
3,5 |
11°)
Idem.
|
10 |
|
15 |
|
27 |
|
|
2,2 |
3 |
4,8 |
|
12°)
La suite de nombres S1
[3,5 ;5,7 ;4 ;9] est proportionnelle à la suite de
nombres S2 [a ;b ;c ;d] Le coefficient de
proportionnalité S1 sur S2 est de
3 . Calculer a ;b ;c ;d
|
|
3,5 |
5,7 |
4 |
9 |
|
k =3 |
|
|
|
|
14 ) La
longueur (L) du cercle est donnée en fonction du diamètre (D); compléter le tableau
suivant :
|
D |
5 |
10 |
12 |
25 |
28,2 |
|
L |
|
|
|
|
|
Les deux grandeurs sont-elles
proportionnelles ?
15 °)
Un cycliste parcourt 12km en 45mn .Un autre 17km en 50mn .Les distances
parcourues sont-elles directement
proportionnelles aux durées du parcours ?
16° ) Trois associés
ont investi dans la même entreprise :le premier :10 000 € ,le deuxième : 14
000 € ;le troisième :26 000 €. Ils ont gagné 13 680€.
Partager le gain proportionnellement aux
mises des associés .