FL 6 généralités

DOSSIER : FONCTIONS LINEAIRES   /  Objectif cours 42

 

Pré requis

 

Fonction "généralités"
Les Grandeurs proportionnelles

 

ENVIRONNEMENT du dossier

 

INDEX warmaths	Objectif précédent : 1°) lire : activité 2°) Graphe d’une fonction	Objectif suivant 1°) Graphe d’une fonction affine	Tableau       1°)La fonction linéaire  (présentation)

DOSSIER Comment  construire Le GRAPHE  de LA FONCTION LINEAIRE

1°) GRAPHE  de la fonction linéaire

2°) Construction d’un graphe à partir de l’équation :

3° ) Obtention d’un graphe à partir d’une représentation graphique

4°) Obtention d’un graphe à partir d’un tableau de variation

5°) Résumé.

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

 

COURS

 

 

MODELES     MATHEMATIQUES  de représentation de la fonction linéaire

 

                   cet objectif traite des généralités sur la fonction linéaire :

                      

                         Une fonction linéaire peut s’identifier à partir de quatre modes de représentation :

A) Equation

B) Graphe

C) Tableau de variation (de proportionnalité)

D) Représentation graphique.

 

 

                           Dans ce cours nous prenons   l’équation:

                                      y = x   est pris  comme exemple.

      (elle est de la  forme « y  =  a x  »   ; dans l’exemple  « a »  =   )

Les transformations possibles :

	Equation	Graphe	Tableau	Représentation graphique
Equation
Graphe
Tableau
Représentation graphique

 

1°) GRAPHE  de la fonction linéaire

 

On peut obtenir un graphe à partir : d’une équation ; d’un tableau de proportionnalité ; d’une représentation graphique.

 

                 Le graphe est un ensemble (ou suite)  de couples de nombres  du type : ()

                       le premier nombre est attribué à « x » appelé « variable »

                       le deuxième nombre est associer au produit  «  ».

                Si « a »  vaut         ,le   couple aura la forme et sera noté :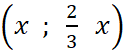   

                        le Graphe de la fonction linéaire se présentera sous la forme :

 G = { ( x₁ ; ax₁) ; (x₂ ;ax₂ ) ; ......... }

 

 

 

2°) Construction d’un graphe à partir de l’équation : y = x

    Obtention d’un couple de nombres  (à partir d’une équation) :

 

On donne une valeur à « x »   (exemple : 9 )

     on obtient un autre nombre  en utilisant l’équation  y = x   ; (y = 9 =(18 :3 ) = 6)

 

en résumé :   si « x » = 9 alors x = 6

      nous obtenons le premier couple de nombres du graphe de la fonction «  » :  (9 ; 6)

 

             On remarque que l’on peut citer  un couple particulier : (0 ;0)   ( en effet si «  » = 0 alors x

Nous obtenons un premier modèle mathématique de la forme :

     G = {  ( 0 ; 0 ) ; ( x₁ ; x₁) ; (x₂ ; x₂ ) ; ......... }

le couple  (x₁ ; x₁)  dans un repère cartésien signifie :

                qu’ à  x₁ on associe  l’abscisse « x »

                qu’ à  « x₁ » on associe  l’ordonnée « y₁ »

 

En modèle « limité »  nous  pouvons utiliser le graphe suivant :

le graphe représentant l ’ équation  y = x   est    G = {( 0 ; 0) ; ( 3 ; 2 ) ;(9 ; 6 ) ; }

 

deux points suffissent  , le troisième point servira pour vérifier si le tracé est « bon »

 

soit le graphe obtenu précédemment G = {( 0 ; 0) ; (9 ; 6 )}

 

ces deux couples de nombres permettent de tracer la représentation graphique de la fonction .

 

 

3° ) Obtention d’un graphe à partir d’une représentation graphique .

 

 

 

 

 

 

 

 

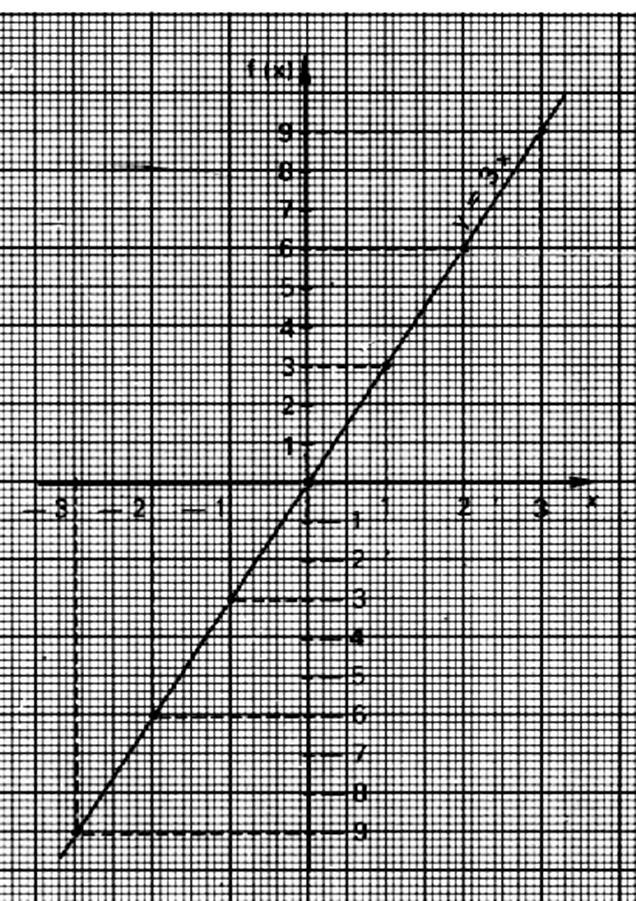
G = { ( -3 ; -9) ; (-2 ;-6 ) ; (-1 ;-3 ) ; ( 0 ; 0 ) ;  (1 ; 3 ) ; (2  ;6 ) ; ( 3 ;9 ) ;  ......... }

 

 

 

4°) Obtention d’un graphe à partir d’un tableau de variation

 

On nous donne le tableau suivant :

		A	B	C	O	D	E	F
		-3	-2	-1	0	1	2	3
		-9	-6	-3	0	3	6	9

Pour construire le graphe il suffit de reprendre les couples de nombres  dans l’ordre croissant de « x » ; ce qui donne le graphe :

 

G = { ( -3 ; -9) ; (-2 ;-6 ) ; (-1 ;-3 ) ; ( 0 ; 0 ) ;  (1 ; 3 ) ; (2  ;6 ) ; ( 3 ;9 )  }

 

 

5°) Résumé.

 

Plus généralement on dira :

                   que le Graphe de la fonction linéaire est de la forme :

 G = {( 0 ; 0 ) ; ( x₁ ; ax₁) ; (x₂ ;ax₂ ) ; ......... }

 

Ce graphe est « fini » si il est obtenu à partir d’un tableau ; il est « infini » si il est obtenu à partir d’une équation ou d’une représentation graphique.

Avec comme les deux couples particuliers :

       

                                                     ( 0 ; 0 )  et  ( 1 ; a ) 

 

 

 

 

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

1°) Donner la forme des couples  qui forment eux mêmes le graphe de la fonction  linéaire.

 

 

2°)  Donner la forme du graphe de la fonction linéaire. ( donner les deux couples particuliers)

 

EVALUATION :

 

1° Etablir un graphe  à partir  d’une représentation graphique.

			Sur la droite on place des points que l’on nomme : A ;B ; C ; O ;D ;E ;F   Le nombre de points est défini à partir de contraintes imposées ! !

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

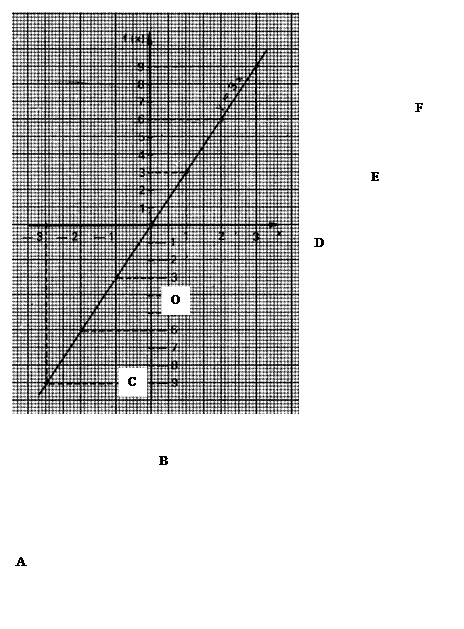
  Pour obtenir la graphe il faut  rechercher  des couples de nombres , ils sont les coordonnées des points fixés .

 

L’ensemble des points A, B ,C ,D, ....              ont pour coordonnés les couples de nombres (x ; 3x )

 

2 ° )   Etablir un graphe à partir de l’équation suivante :  «  y = 3x « 

 

 

(il peut compter un infinité de couples : le minimum est de 3 couples  )

 

 

3° ) soit le tableau de proportionnalité suivant ; donner le graphe

 

		A	B	C	O	D	E	F
3 x	x	-3	-2	-1	0	1	2	3
	y	-9	-6	-3	0	3	6	9