|
Fractions équivalentes
(égalité de deux fractions) |
Environnement du dossier :
|
Objectif précédent : |
DOSSIER : L’égalité de
deux fraction est le : PRODUIT EN CROIX
|
|
COURS |
Devoir évaluation |
Interdisciplinarité |
|
IMPORTANT:
Comment vérifier si deux fractions sont équivalentes ? on fera
« le produit en ...croix » .
Procédure permettant de vérifier si deux fractions sont équivalentes:
Pour
s’assurer (ou vérifier) que
deux fractions sont
équivalentes, il suffit de transformer l’égalité des deux fractions.
1°) On transforme ce l’égalité
mathématique ci dessous :
=
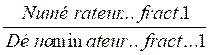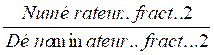
en une autre égalité de deux produits: : Numérateur..fract.1 x Dénominateur .fract. 2 =
Numérateur fract.2 x Dénominateur fract 1
que l’on appelle « égalité de deux produits » , obtenue en faisant le produit en croix .
2°) On effectue les multiplications
3°) et on compare les résultats
4°) On conclut:
a) si les produits sont égaux ;les fractions sont dites équivalentes.
b) si les produits ne sont pas égaux ;les
fractions données ne sont pas égales
Exemple: On reprend l’exercice
précédent:
Enoncé : La fraction 22 /30
est-elle équivalente à la fraction
583/795 ?
On applique la procédure:
► On énonce:
est égale à 
si 22 x
795 est égal à 583 x 30
► On effectue les
calculs:
22 x
795 =
17 490 et 583 x
30 = 17 490
►On compare les résultats :
22 x 795 est égal
à 583 x 30 ( 17490=17490)
► On tire une Conclusion: les
fractions et sont
équivalentes; se qui se traduit
par l’égalité : =
En résumé:
Deux fractions (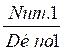
et 
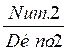) sont
équivalentes (c’est à dire) : 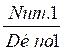= 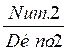si Num.1 x
Déno.2 = Num.2 x Déno.1
Traduction
en langage littérale:
Deux fractions sont équivalentes
si le produit du numérateur de la première fraction par le dénominateur de la
seconde fraction est égal au produit du numérateur de la deuxième fraction par
le dénominateur de la première fraction.
Remarques importantes:
On appelle cette méthode : le produit en croix.
Lorsque nous aborderons la lecon sur les
proportionnalités on dira:
que le produit des extrêmes est égal au produit des moyens ,
(les extrêmes étant Num.1 et Déno.2, les moyens étant Déno.1 et Num.2)
= 
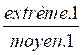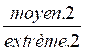si extrème.1
x extreme.2 =
moyen.1 x moyen.2
Applications :algèbre
« résoudre »
avant
de résoudre il faut transformer l ‘égalité donnée ;en appliquant le produit en croix
|
|
|
|
|
|
|
|
|
|
5x
=12 |
|
7 |
|
7x=3 |
|
7 |
|
3|
Utiliser pour calculer la quatrièmes proportionnelle |
Cliquer ici |
La
règle de trois
La règle de trois s ’ applique
à la forme mathématique :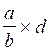 
= ? (=
c )
Cette écriture doit se transformer sous la forme =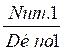
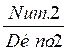
tel
que : 
=
; l ‘ égalité est
vraie si : ad = b c
Nous obtenons le produit « en croix » suivant : a 
d = c b
CALCULS PARTICULIERS
forme : « une fraction
est égale à un nombre »
= c ; on
recherche ou « a » ou « b »
Alors
faire la transformation : = 
est effectuer le produit en croix .tel
que : a 1 = c b ;soit :
a = cb
ou = devient 
= b ;pour
obtenir b = 
EXERCICES :
Transformer l’égalité , par le produit en croix Lne pas
faire le calcul , c’est à dire « ne
pas résoudre » )
a )
= 5
; b
) 
= 7 ;
réponses :
a) x = 13 5 ;
b )
13 = 7 x
TRAVAUX AUTO FORMATIFS.
1° ) Dans quel domaine des
mathématiques utilise-t-on les fractions équivalentes ?
2 ° ) Par quel signe sont séparées deux fractions
équivalentes?
3° ) Que représente deux
fractions équivalentes , autre qu ‘une égalité ?
4 ° ) Donnez le modèle
mathématique représentant deux fractions équivalentes.
5 ° ) Donnez la
procédure permettant d’obtenir une fraction équivalente à une fraction
donnée,donnez le modèle mathématique.
6° ) Comment peut-on
procéder pour ordonner ( classer dans un
ordre croissant ou décroissant ) des fractions
?
7° ) Comment procède -t
- on pour vérifier si deux fractions sont équivalentes ?
8 ° ) Enoncer la
procédure permettant d’effectuer « le produit en croix ».
I) On nous donne deux fractions ;
et 
;sont-elles
équivalentes? (prouvez le )
II ° ) CALCUL
ALGEBRIQUE :
Transformer , par le produit en croix , les
fractions équivalentes :
|
|
|
|
|
|
|
|
|
et encore :
a) = 5
b) = 7 ;