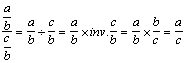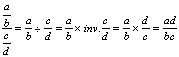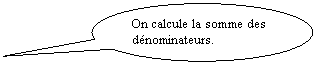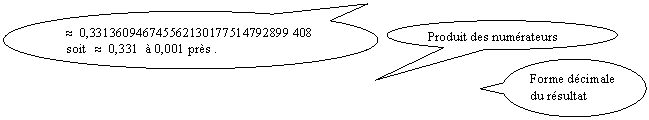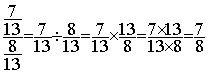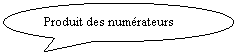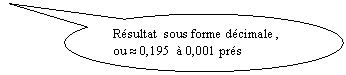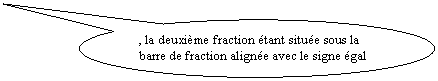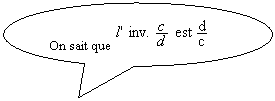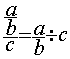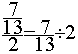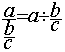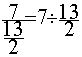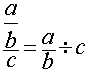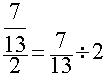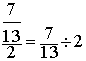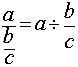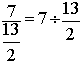|
Leçon
|
Titre
|
|
N°5
|
LES FRACTIONS :
Opérations : Addition ;
soustraction ; multiplication ; division
|
Important :Pour faciliter les calculs et pour éviter les risques d’erreurs de
calcul , il est conseillé de simplifier
jusqu’à rendre irréductible la ou
les fractions .
* chaque opération est traitée, à chacune correspond une
information plus particulière .
|
Définition : La somme de deux fractions est égale à
une troisième fraction qui aura pour
« Numérateur » : la somme des numérateurs et pour
« Dénominateur » : le dénominateur commun.
|
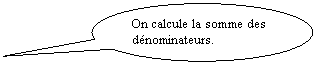 .
.
Forme mathématique:

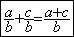
Exemple
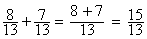
Règle :
(Forme
littérale)
|
Définition : La différence de deux fractions est égale
à une troisième fraction qui aura pour
« Numérateur » : la différence des numérateurs et pour
« Dénominateur » : le dénominateur commun.
|

Forme
symbolique mathématique:
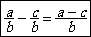
Exemple
 Calcul de :
Calcul de : 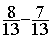
 Solution :
Solution : 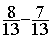 =
= 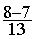 =
= 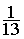
Expression
du résultat :
Conclusion : 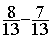 =
= 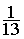 ; »
0,333333333333333333333333333333333
; »
0,333333333333333333333333333333333

Règle : ( Forme littérale)
|
La
multiplication de deux fractions de même dénominateur est égale à une
troisième fraction qui aura pour: « Numérateur » le produit des
numérateurs et pour « Dénominateur » le produit des dénominateurs.
|

Forme
symbolique mathématique:

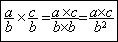

Exemple :
Calcul de 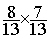
Solution : 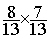 =
= 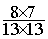 = ou
=
= ou
= 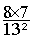
Calculs : 8
fois 7 = 56 et 13² = 169
Soit : 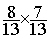 =
= 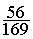
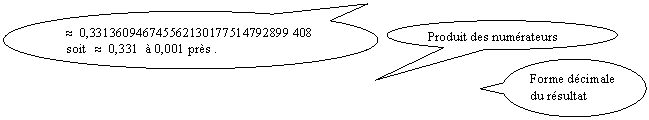
En
conclusion 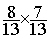 =
= 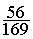 ou » 0,331
ou » 0,331
 Remarque
importante: Nous ne pouvons pas calculer directement la fraction de
deux fractions ,il faut impérativement transformer
Remarque
importante: Nous ne pouvons pas calculer directement la fraction de
deux fractions ,il faut impérativement transformer
Donc
l’écriture : 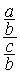 se
transforme en
se
transforme en 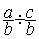
 La fraction de deux fractions
La fraction de deux fractions 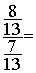 devient
devient 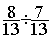
Bien que la fraction de deux fractions soit transformée en
division ;le calcul de
la division de deux fractions ne se fait pas ; il faut « passer » par la multiplication en
respectant la procédure suivante:
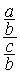 se transforme en
se transforme en 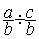 qui
devient
qui
devient 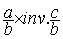 =
= 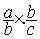 =
= 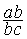 =
=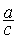
En conclusion : 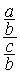 =
= 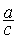
En
résumé :
|
Règle : ( forme littérale ) Pour
calculer la division de deux fractions il suffit de
multiplier la première fraction par l’inverse de seconde
fraction.
|
Autrement
dit : Le résultat de la division de deux fractions de même
dénominateur est égal au produit de la
première fraction par l’inverse de seconde fraction .
Forme
symbolique mathématique :
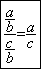
Exemple :
calculer 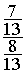

Solution :
 Déroulement :
Déroulement : 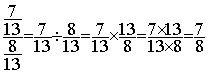
Conclusion : 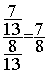 = 0,875
= 0,875
+Faire les exercices
suivants :
|
Addition
|
|
|
|
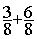 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs)
|
|
|
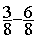
|
|
|
|
Soustraction
|
|
|
|
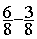 = =
|
|
|
|
Multiplication
|
|
|
|
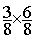 = =
|
|
|
|
Fraction de fractions
|
|
|
|
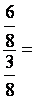
|
|
|
|
Division de fractions
|
|
|
|
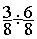 = =
|
|
|
Réponses : 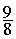 ;
; 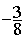 ;
; 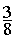 ;
; 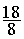 ;
; 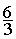 ;
; 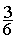
Il faut
valider les acquis précédents avant d’étudier le chapitre « B »
(chapitre suivant)
|
i9
voir ci- dessus.
i29
|
B ) ADDITION ;
SOUSTRACTION ; DIVISION et
MULTIPLICATION ; de DEUX
FRACTIONS de DENOMINATEURS DIFFERENTS.
|
:i
Cd³ INFO +
|
 Soit les deux fractions
Soit les deux fractions 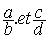 On ne peut pas additionner des
fractions de dénominateurs différents :
On ne peut pas additionner des
fractions de dénominateurs différents :

Ainsi
avant de faire l’addition de deux fractions il faut transformer
chaque fraction en fraction dite « équivalente »
dont le nouveau dénominateur est égal
au produit des deux dénominateurs « bd » .

a) 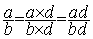
 b)
b) 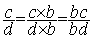
On remplace l’addition 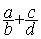 par
par 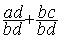

On peut écrire
l’égalité : 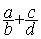 =
= 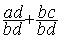
On peut maintenant effectuer l addition des deux fractions:
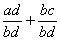 =
=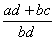
Exemple : Calculer 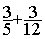
Procédure :
1°) Au préalable on simplifie ou ,dans la mesure du
possible’ on essaie de rendre irréductible
la ou les fractions :
ce qui est le cas de pour 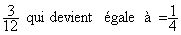
2°) On
remplace l’addition 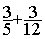 devient égale à
l’addition
devient égale à
l’addition 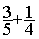
On a remplacé 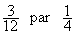 , On obtient
une nouvelle addition ,
, On obtient
une nouvelle addition ,
3°) On calcule le « dénominateur commun » :
5 fois 4 = 20
4°) Transformation
chacune des deux fractions
. (Dont le dénominateur sera
20)

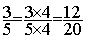 ;
; 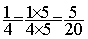
5°) On remplace l’addition avec
les fractions de départ par une nouvelle addition avec des fractions équivalentes :
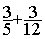 =
= 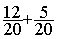
Nous avons maintenant
deux fractions de même dénominateur , nous pouvons
faire l’addition .
6°) Calcul de l’addition :
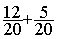 =
= 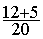 =
= 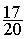
7°) Conclusion :
|
On reprend l’énoncé : l’addition de
départ !
|
On donne le résultat sous
forme irréductible
|
On peut donner aussi le
résultat sous forme décimale
|
|
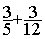 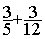
|
= 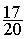
|
= 0,85
|
8°) Vérification : Dans tous les cas il
faut vérifier si notre résultat est
conforme ; pour cela on calcule la
division dans chaque fraction :
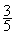 = 3 ¸ 5 = 0,6
;
= 3 ¸ 5 = 0,6
; 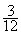 = 3 ¸ 12 = 0,25
= 3 ¸ 12 = 0,25
Ensuite , on
remplace les deux fractions par les valeurs décimales calculées
précédemment et l’on compare :
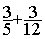 =
0,6 + 0,25 = 0,85
=
0,6 + 0,25 = 0,85
On compare 0,85 avec 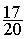 , bien
entendu nous trouvons le même nombre
donc on peut maintenant conclure que :
, bien
entendu nous trouvons le même nombre
donc on peut maintenant conclure que :
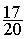 =
= 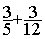
Soit les
deux fractions 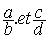 On ne peut pas soustraire des fractions de dénominateurs
différents :
On ne peut pas soustraire des fractions de dénominateurs
différents :
Ici le
dénominateur commun sera «
bd »
On doit
transformer les fractions en fractions équivalentes dont on donnera un
dénominateur égal au produit des dénominateurs.
Avant de faire une soustraction il faut :
Transformer chaque
fraction en fraction dite
« équivalente » dont le nouveau dénominateur est « bd » .

a) 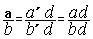
 b)
b) 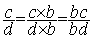
 On
remplace
On
remplace 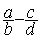 par
par 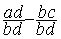
On peut écrire 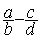 =
= 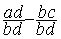
On peut maintenant effectuer la soustraction des deux fractions:
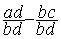 =
=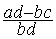
Exemple :
Calculer 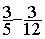
 Procédure :
Procédure :
1°) Rendre irréductible la ou les
fractions : ce qui est le cas de 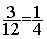
2°) réécrire la nouvelle opération : 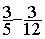 devient égal à
devient égal à
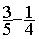
3°)calculer
le dénominateur commun : 5 fois 4
= 20
4°) Transformation les deux
fractions de départ par des fractions équivalentes , ayant toutes deux un même dénominateur .

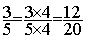 ;
; 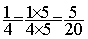
5°) Remplacer les fractions de la
soustraction d’origine par les fractions équivalentes :

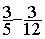 =
= 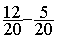
6°) calcul de la soustraction :
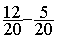 =
= 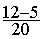 =
= 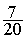
7°) 1ère conclusion :

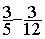 =
= 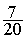 =
0,35
=
0,35
8°) Vérification : 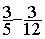 = 0,6 -
0,25 = 0,35 ; et
= 0,6 -
0,25 = 0,35 ; et 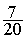 =
0,35 ; conclusion
=
0,35 ; conclusion
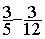 =
= 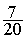
|
Si l’addition et la soustraction de deux
fractions de dénominateurs
différents posent un réel
problème , il n’en est pas de même
pour la multiplication et la division ( ou fraction ) de
fractions : il n’y a aucune transformation particulière , il faut
appliquer directement les
règles énoncées pour les fractions de même dénominateur .
|
Voir suite du cours .
Il n’y a
pas de transformation particulière
à effectuer , ainsi la multiplication de deux fractions de dénominateur
différent ne pose pas de problème
particulier .
On retiendra la règle suivante :
|
Règle : ( écriture
littérale)La
multiplication de deux fractions de dénominateur différent est égale à une
troisième fraction qui aura pour
« Numérateur » : le produit des numérateurs et pour
« Dénominateur » : le produit des dénominateurs.
|
Traduction
symbolique mathématique: 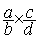 =
= 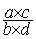 =
= 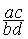
 Exemple : calculer :
Exemple : calculer : 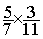
Solution :

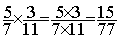

conclusion : 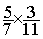 =
= 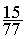 » 0,194805194805194805194805194805195
» 0,194805194805194805194805194805195
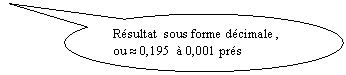
 iNous ne pouvons pas calculer directement la fraction de
deux fractions ,il faut impérativement transformer
l’écriture .
iNous ne pouvons pas calculer directement la fraction de
deux fractions ,il faut impérativement transformer
l’écriture .
 Donc
l’écriture :
Donc
l’écriture : 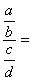 se transforme en
se transforme en 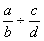
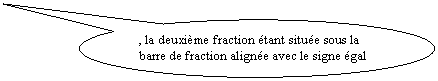 La fraction de fractions
La fraction de fractions 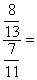 devient
devient 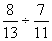
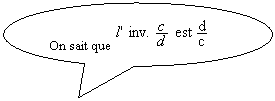 Bien que
la fraction de fractions soit transformée en division ; la division de deux
fractions ne se fait pas ; il faut transformer la division en multiplication en respectant
la procédure suivante:
Bien que
la fraction de fractions soit transformée en division ; la division de deux
fractions ne se fait pas ; il faut transformer la division en multiplication en respectant
la procédure suivante:
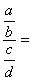 se
transforme en
se
transforme en 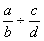 qui
devient
qui
devient 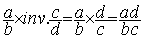
En conclusion : 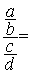
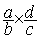
Et l’on applique ,ensuite, les règles de la multiplication de deux
fractions.
|
Règle : ( forme littérale ) Pour
calculer la division de deux fractions il suffit de
multiplier la première fraction par l’inverse de seconde
fraction.
|
Forme symbolique
mathématique :
Exemple : 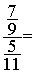
 ( »0,244444444444444444444444444444444)
( »0,244444444444444444444444444444444)
conclusion : 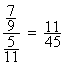 ; »0,24 à 0,01
près ( il faudrait faire la vérification ! !)
; »0,24 à 0,01
près ( il faudrait faire la vérification ! !)
+Faire les
exercices suivants
|
Addition
|
|
|
|
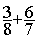 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs
|
|
|
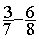 = =
|
|
|
|
Soustraction
|
|
|
|
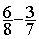 = =
|
|
|
|
Multiplication
|
|
|
|
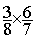 = =
|
|
|
|
Fraction de fractions
|
|
|
|
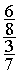 = =
|
|
|
|
Division de fractions
|
|
|
|
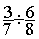 = =
|
|
|
iComme vous
l’avez remarqué :
on peut multiplier ou
diviser directement deux fractions de
dénominateur différent , on ne peut pas additionner ou
soustraire deux fractions qui
n’ont pas le même dénominateur .
Addition d’une fraction avec un nombre entier
(naturel ou relatif)
Modèle mathématique: 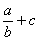 = ?
= ?
 Exemple:
Exemple: 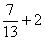 = ?
= ?
idans
l’addition , Que le nombre soit devant
ou derrière la fraction le résultat ne changera pas : 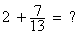 ( cela ne
sera pas vrai avec la soustraction )
( cela ne
sera pas vrai avec la soustraction )
Procédure pour transformer l ‘ addition
( ou la soustraction ) en addition ( ou soustraction) de deux
fractions de même dénominateur.
1°)Rendre la
fraction
irréductible.:
Exemple : 7 /13
= 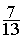
2°)Mettre le nombre
sous forme de fraction de dénominateur égal à
1
Modèle mathématique: c = 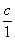 ;
Exemple : 2
=
;
Exemple : 2
= 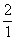
3°)Transformer cette fraction en fraction
équivalente de dénominateur égal au dénominateur de la première
fraction.
Modèle mathématique: 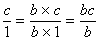
Le dénominateur de la première fraction est 13
donc 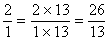 =
=
4°) Poser la nouvelle égalité
Modèle mathématique: 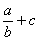 =
= 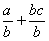
donc 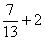 =
= 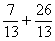
5°) Faire l’addition des deux fractions de même dénominateur. 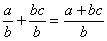
donc 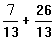 =
= 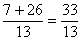
6° ) il faudra conclure (comme on l’a vu pour les
exercices précédents ), après vérification.
Soustraction d’une fraction avec un nombre entier
(naturel ou relatif)
 Modèle mathématique:
Modèle mathématique: 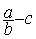 = ?
= ?
 Exemple:
Exemple: 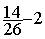 = ?
= ?
iContrairement
à l’addition , pour la soustraction , si l’on permute
le nombre et la fraction on n’aura pas
le même résultat: 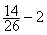 ¹
¹ 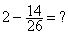
Procédure pour transformer la
soustraction d’un nombre et d’une
fraction en soustraction de deux fractions de même dénominateur.
( nous ne
traiterons que l’exemple de
soustraction : 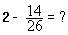 )
)
procédure :
1°)Rendre
la fraction
irréductible.:
Exemple : la fraction irréductible de 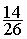 est
est 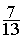
2°)Mettre le nombre
sous forme de fraction de dénominateur égal à 1
Modèle mathématique: c = 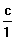 ;
exemple : 2 =
;
exemple : 2 = 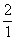
3°)Transformer cette fraction en fraction
équivalente de dénominateur égal au
dénominateur de la première fraction.
Modèle mathématique: 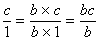
Le dénominateur de la première fraction est 13
donc 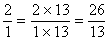
4°) poser la nouvelle égalité
Modèle mathématique: 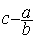 =
= 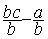
donc 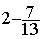 =
= 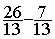
5°) faire la soustraction des deux fractions de même
dénominateur.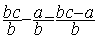
donc 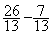 =
= 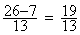
6° ) il faudra conclure (comme on l’a vu pour les
exercices précédents ), après
vérification.
|
Par définition : On ne
peut pas multiplier un nombre par une fraction ,
pour obtenir un résultat on prendra appui sur la règle concernant la
multiplication de deux fractions .
|

Modèle mathématique: 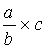 =
=
Exemple : 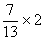 = ? ;
= ? ;
On passe de ce
modèle mathématique: 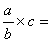 à ce modèle
à ce modèle 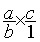
Remarque : Il faut mettre le nombre
« c » sous forme de fraction de dénominateur égal à 1
; tel que c =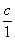
3° ) On
applique la procédure concernant la multiplication de deux fractions:

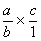 =
=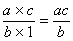
4° )
Rendre compte: 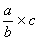 =
=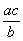
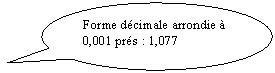 Exemple :
Exemple : 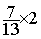 =
=
Solution : 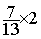 =
= 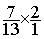 =
= 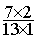 =
= 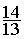
Conclusion :
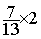 =
= 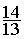
Cas particulier 1 : on veut calculer : 3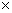
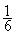 = ;
= ; 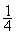
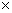 72
72
Modèle mathématique: 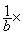 a = pas de
solution immédiate ; (il faut
transformer)
a = pas de
solution immédiate ; (il faut
transformer)
Exemple : si
b = 2
Exemple 1 : Calculer 3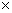
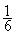 = ? ( donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale )
= ? ( donner le résultat sous forme d’une fraction simplifiée ; puis
sous la forme décimale )
3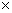
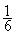 =
= 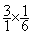 ( voir multiplication de deux fractions)
( voir multiplication de deux fractions)
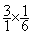 =
= 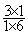 ;
; 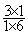 =
=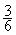 (voir
simplification d’une fraction)
(voir
simplification d’une fraction)
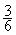 =
= 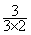 ;
; 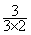 =
= 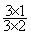 ;
; 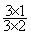 =
= 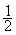
conclusion : 3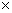
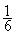 =
= 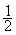 ; remarque :
(
; remarque :
(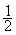 = 0,5 ),
sous forme décimale 3
= 0,5 ),
sous forme décimale 3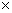
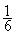 = 0,5
= 0,5
Exemple 2 : calculer
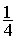
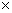 72 ( donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale )
72 ( donner le
résultat sous forme d’une fraction
simplifiée ; puis sous la forme décimale )
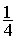
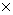 72 =
72 = 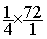 =
=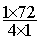 ;
; 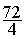 =
= 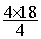 ;
; 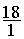
Conclusion : 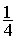
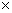 72 =
72 =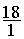 ou
ou 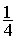
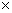 72 = 18
72 = 18
En
résumé : On ne peut pas multiplier un
nombre par une fraction , pour obtenir un résultat on
prendra appui sur la règle concernant la multiplication de deux fractions.
Procédure permettant de multiplier
une fraction par un nombre.( Modèle mathématique: 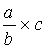 = ) Il faut faire dans l’ordre :
= ) Il faut faire dans l’ordre :
a) Placer le nombre sous forme de
fraction de dénominateur égal à 1 : 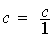
b) On passe de ce modèle
mathématique: 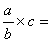 à ce modèle
à ce modèle 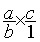
c) On applique la procédure
concernant la multiplication de deux fractions:
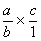 =
=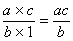
d ) Rendre
compte: 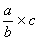 =
=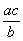
Attention: on ne doit pas confondre:
« diviser une fraction par un nombre(
entier) » ( 1° cas):
ET
« diviser un nombre ( entier) par une
fraction »(2° cas)
iCe qui
différencie les deux cas est la position du signe « égal »
devant l ‘ une des deux barres de
fraction :
Etude
du 1° cas : « diviser une fraction par un nombre(
entier) »
 1°) Première transformation
1°) Première transformation
Exemple: 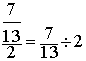
2°) Deuxième transformation
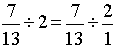
 3°) Troisième
transformation : seconde. »
3°) Troisième
transformation : seconde. »
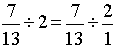 =
= 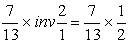
4°) Calcul : appliquer la règle concernant la
multiplication de deux fractions.

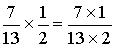 =
= 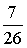
Etude du second cas : Division d’un nombre "a" entier
par une fraction

 Exemple :
Exemple : 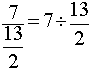
1°) Transformer la division d’un nombre par une
fraction en une division de fraction par
une fraction.
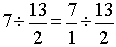
2°) Multiplier la première fraction par l ‘inverse de
la seconde. »
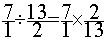
4°) Faire la
multiplication des deux fractions.

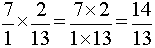
ion peut constater
que les deux cas donnent des résultats différents ,il est donc trés important de vérifier la position du signe
« égal »
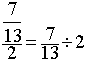 donne
comme résultat:
donne
comme résultat: 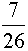 » 0,……
» 0,……
et 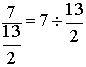 donne comme
résultat:
donne comme
résultat: 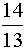 » 1,……
» 1,……
+Faire les
exercices suivants
|
Addition
|
|
|
|
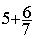 = =
|
|
|
|
Soustraction ( pour cet exercice il faut avoir fait la leçon sur les
nombres relatifs)
|
|
|
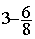 = =
|
|
|
|
Soustraction
|
|
|
|
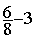 = =
|
|
|
|
Multiplication
|
|
|
|
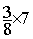 = =
|
|
|
|
Fraction de fractions
|
|
|
|
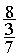 = =
|
|
|
|
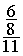 = =
|
|
|
|
Division de fractions
|
|
|
|
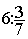 = =
|
|
|
|
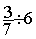 = =
|
|
|
Cd³ INFO
+
( Voir la partie
abordée dans la leçon N°2 sur la fraction)
 A
savoir : a% =
A
savoir : a% = 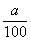

y = 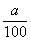 x ;
ou y =
x ;
ou y = 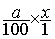 =
= 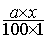 =
= 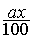
ou
« y » est la valeur
d’une augmentation ou diminution
« a » la
valeur du taux
« x » le nombre sur lequel
s’applique le taux.
Exemple : on veut
calculer 8 % de 120
On transforme :
8% = 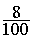 ( = 0,08 )
( = 0,08 )
On calcule : 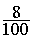 ´ 120 =
´ 120 =  =
= 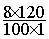 =
= 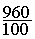 = 9,6
= 9,6
Conclusion :
8% de 120 = 9,6
![]()