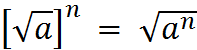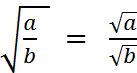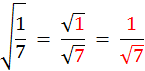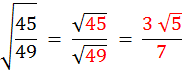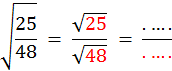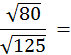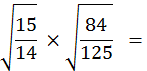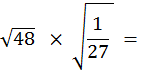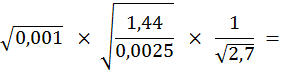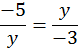corrigé _Troisième - Les RACINES carrées au collège . Fiches pédagogiques

	Programme classe de 3^ème collège.	3^ème collège. (2015)
Retour vers les fiches
	CORRIGE
Pré requis:
Vocabulaire : les radicaux
Le "carrée" parfait

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent

Le « carré » d’un nombre

Objectif suivant

1°)Racines carrés d’opérations simples

2°) extraction d’une racine carrée

3°) la table numérique

1°) Tableau 79

2°) liste des objectifs sur les puissances et racines

3°) Cours niveau V

4°) Racines cubiques

5°) encadrement d’un résultat

Fiches 3^ème collège sur les : RACINES CARREES.

	Fiche 1 : Longueur du côté d’un carré dont on connaît l’aire.
	Fiche 2 : Racine carré d’un nombre positif.
	Fiche 3 : Comparaison des carrés et racines carrées de nombres positifs.
	Fiche 4 : Résolution de l’équation « »
	Fiche 5 : Racine carrée du carré d’un nombre .
	Fiche 6 : Exercices divers.
	Fiche 7 : Racine carrée d’un produit.
	Fiche 8 : Racine carrée d’un quotient.
	Fiche 9 : Somme algébrique où figure des radicaux.
	Fiche 10 : Résolution d’équations et de problèmes.
	Fiche 11 : Exploitation de données statistiques.

TEST

écran

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Travaux avec la calculatrice : taper des valeurs et comparer le résultat donné par la table numérique

Définition de l’objectif : Savoir « donner » le radical d’un nombre.. (On dit aussi donner la racine « carrée ou cubique d’un nombre »)

Rappel nous abordons la racine carrée d’un nombre entier naturel ; ne pas confondre avec la racine carrée d’un nombre relatif…

Fiche 1 : Longueur du côté d’un carré dont on connaît l’aire.

Info + @ aire du carré….

Vous savez calculer l’aire d’une surface carrée.

Si la mesure en cm du côté est « 7 » , la mesure de l’aire en cm² est : 7² = 49

Si la mesure en cm du côté est « » , la mesure de l’aire en cm² est :

Inversement :

La mesure en cm² de l’aire d’un carré est « 49 » , la mesure en « cm » est … 7 ….

La mesure en cm² de l’aire d’un carré est « 81 » , la mesure en « cm » est … 9 ….

La mesure en cm² de l’aire d’un carré est « 0,25 » , la mesure en « cm » est … 0,5 ….

La mesure en cm² de l’aire d’un carré est « 29 » , déterminons , si cela est possible, la mesure en « cm » du côté de ce carré . ( Etant une mesure , ce nombre est positif ).

Appelons « » le nombre positif cherché. On doit avoir

Vous savez ( voir cours de 4^ème) que les nombres positifs sont rangés dans le même ordre que leurs carrés.

Plaçons « 29 » dans la suite des carrés des entiers successifs.

; donc « » n’est pas entier.

Il est possible de démontrer que ce nombre n’est pas un décimal et que l’on ne peut pas l’écrire sous la forme avec « a » et « b » entiers, mais il est possible d’en donner des valeurs approchées décimales.

Remarque : ce nombre est unique car deux surfaces carrées dont les côtés ont des longueurs différentes ne peuvent pas avoir la même aire.

Valeurs approchées décimales de « » tel que « »

On a vu que : . On va chercher par tâtonnement des encadrement de « ».

· Encadrement de « » par des décimaux à 10^-1 prés :

5,3 ² = 28,09

5,4 ² = 29,16

5 ,3 ² < 29 < 5,4 ²

Donc : …5,3……< < …5,4…….

· Encadrement de « » par des décimaux à 10^-2 prés :

5,38 ² = 28,9444

5,39 ² = 29,0521

5 ,38 ² < 29 < 5,39 ²

Donc : …5,38…< < …5,39….

· Encadrement de « » par des décimaux à 10^-3 prés :

5,38.. ² = ………..

5,38 …… ² = ………

………….. < 29 < …………

Donc : ……< < …….

Et l’on peut continuer indéfiniment…………………..

Activité :

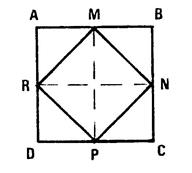
ci-contre est un carré noté « ABCD » de 2 cm de côté.

M,N, P , R sont les milieux des côtés.

Démontrez ( verbalement) que « MNPR » est un carré.

Déterminez l’aire du carré « MNPR ».

Vous trouvez : ………………………………………

Appelons « L » la mesure en « cm » de la longueur du côté du carré « MNPR ».

On peut écrire alors L² = ………………….

racine_carr001

( Le nombre « L » existe bien puisque on a pu dessiner un carré de côté « L » )

Déterminez par tâtonnement ( comme précédemment) un encadrement de « L » à 10 ^-3 prés . ( Contrôlez en mesurant sur la figure )

Fiche 2 : Racine carré d’un nombre positif.

Info +++@ ++++

On a vu que Lfiche 1)

Il existe un entier naturel « u » tel que « u² = 81 » , ce nombre est « u = 9 »

Il existe un décimal positif « v » tel que « v² = 0,25 » , ce numéro est « v = 0,5 »

On dit que « 9 » est la racine carrée de « 81 » . « 0,5 » est la racine carrée de « 0,25 » …..

….. et on écrit (au collège) : ( on lit « racine carrée de « 81 » égal « 9 » ) .

· De même ; dans le cas de « x² = 29 » , et bien qu’on ne puisse en donner une écriture décimale ou fractionnaire , on écrit « »

· Le nombre positif « L » tel que « L = 2 » s’écrit L =

Définition :

Etant donné un nombre positif « » , on appelle « racine carrée de « » noté , le nombre positif (unique) dont le carré est égal à « ».

« a » et « x » étant des nombres positifs , « » signifie que « »

Vocabulaire : le symbole « » se lit « radical ». Dans l’écriture « » , « a » s’appelle le « radicande ».

Au lieu de dire « racine carrée de « » » on dit parfois « radical de « » ».

Remarque 1 : puisque , et qu’un carré est toujours positif, alors « a » est …positif….. donc « » n’a une signification que si « a » est positif . Aussi : « » ne signifie rien.

Remarque 2 : Il existe deux nombres relatifs tel que « ».

Ces deux nombres sont (+6) et ( - 6 ).

Mais seul le nombre positif est appelé « racine carrée »

mais

« a » étant un nombre positif , « » est positif , « » est négatif , « » est l’inverse « »

Activité : Parmi les égalités ci-dessous , barrez celles qui sont fausses ou incorrectes.

Recherche de la racine carrée d’un nombre positif.

Info ++@ ++extraction d’une racine carrée+

Vous avez déjà vu que ou que .

De même , puisque alors .

· Complétez :

· Dans le cas de , on ne peut pas trouver d’écriture décimal ou fractionnaire, on se contente de donner des valeurs approchées décimales.

Pour cela , on peut utiliser la touche

d’ une calculatrice.

Dans le cas de , la calculatrice de l’ordinateur donne : 5,3851648071345040312507104915403

On peut écrire alors ( par exemple ) un encadrement à 10 ^-3 prés : …5,385.. < 29 < ……5,386……

Attention : la valeur « 5,3851648071345040312507104915403 » n’est pas la valeur exacte de la racine carrée de « 29 ».

Si l’on effectue le produit 5,3851648071345040312507104915403 5,3851648071345040312507104915403 = trouvera –t-on « 29 » ?

on trouve :28,99999999999999999999999999926

Donc : la valeur exacte de la racine carrée de « 29 » est le nombre qui s’écrit .

Activités :

En utilisant la calculatrice , compétez le tableau ci-dessous.

Vérifiez les deux premiers cas donnés en exemple.

nombre

361

79,21

0,2357

Racine carrée exacte

Racine carrée approché à 10^-3 près par défaut.

4,123

Fiche 3 : Comparaison des carrés et racines carrées de nombres positifs.

Vous savez que , dans l’ensemble des nombres positifs , les nombres sont rangés dans le même ordre que leurs carrés.

A retenir :

« a » et «b » étant des nombres positifs , dire que « a > b » c’est dire que « a² > b² »

· « a » et «b » étant des nombres positifs ,

Si « a = b » , « a » est le même nombre que « b » , or un nombre n’a qu’un carré , donc « a² b² »

Si « a b » , alors « a > b » ou « a < b » donc « a²> b² » ou « a² < b² » donc « a² b² »

Si « a² = b² » , on ne peut pas avoir « a b » . Par conséquent , si « a² = b² » alors « a b »

A retenir :

« a » et «b » étant des nombres positifs , dire que « a = b » c’est dire que « a² = b² »

· « a » et «b » étant des nombres positifs , , puisque « )² = a » et « )² = b » , alors dire que « a = b » , c’est dire que « )² = )² », c’est dire que « ) = ) ».

A retenir :

« a » et «b » étant des nombres positifs , dire que « a = b » c’est dire que « ) = ) ».

· dire que « a > b » , c’est dire que « )² > )² », c’est dire que « ) > ) ».

A retenir :

« a » et «b » étant des nombres positifs , dire que « a > b » c’est dire que « ) > ) ».

Activités :

Rangez dans l’ordre croissant :


Fiche 4 : Résolution de l’équation « »	Info : +++@ ++
Un carré est toujours positif, l’équation « » d’inconnue « » ne peut avoir de solution que si « » . · si « » , l’équation « x² = 0 » possède la solution unique « 0 ». · si « » , résolvons , par exemple, l’équation « » d’inconnue « ». Puisque « 7² = 49 » , alors « 7 » est solution de l’équation « ». D’autre part, vous savez que « 2 » nombres opposés ont le même carré , donc « -7 » est aussi solution de l’équation.

· Résolvons l’équation « x² = 29 ». · Vous savez que le nombre est tel que ( , donc est solution de l’équation « x² = 29 ». « - » , l’opposé de « + », est aussi solution car « ( - = 29 » · D’une manière générale , « a » étant un nombre positif , l’équation « » d’inconnue « x » possède la solution « » puisque « )² = a » et la solution « » puisque « )² = a » , il est possible de démontrer qu’elle ne possède pas d’autres solutions.

Théorème : « » étant un nombre relatif, considérons l’équation « » d’inconnue « » . Si « a < 0 » l’équation n’a pas de solution. Si « a = 0 » l’équation possède la solution unique « 0 ». Si « a > 0 » l’équation possède deux solutions «….. » et «….. » .

Activités : L’équation « x² - 9 = 0 » a les mêmes solutions que « x² = 9 » c'est-à-dire ( + 3 ) et (- 3 ) .

Résolvez l’équation : x² - 5 = 0		Résolvez l’équation : 9 x² - 25 = 0
Résolvez l’équation : x² + 6 = 0		Résolvez l’équation : 7 x² - 2 = 0

Fiche 5 : Racine carrée du carré d’un nombre .

« a » étant un nombre positif , vous savez que « )² a » , mais que pouvez-vous dire de « » ? .

Exemple : « »

« a » étant un nombre positif , « » est le nombre dont le carré est égal à « a ».

Or le seul nombre positif dont le carré est égal à « a² » est « a » . On dira alors :

Si « a 0 » alors )² a

Cas ou « a » est un nombre négatif.

Exemple : « a = -3 » ; = = ( 3 ) . Vous constatez que ( - 3 )

Bien que « a » soit négatif , )² a toujours une signification car « a² » est positif.

Mais dans ce cas : )²

Puisque « » alors « » et comme , on dira alors :

Si « » alors « »

Activités 1 : complétez :

= ……………….

= ……..

Activité 2 : Complétez le tableau .

« »

-3


Fiche 6 : Exercices divers.

Activité 1 : Donnez la valeur exacte ou un encadrement par des valeurs approchées à « 1 près » de :
=	< …………..


Activité 2 : Si cela est possible , déterminez « » ou donnez une écriture simplifiée de « ». ( donnez toutes les solutions) .
« x = )² »	; x = …5…..
« x² = 49 »		« x ² = »
		« »
« x =		« »
( - x ) ² = - 36		« »
= 8
« x = »		« x = »
« x² = »		« »
= -7
( - x ) ² = 9		« »
« x = - »
« x = (		« - »
« x² = - 4 »


Fiche 7 : Racine carrée d’un produit.		Info ++ @ +++++


Vous constatez que :
« a » et « b » étant des nombres positifs. , , , existent et sont positifs. Nous allons démontrer que : = . Pour cela , calculons ( = ; = , donc ( Les nombres positifs : et ayant leurs carrés égaux sont donc égaux..
Théorème : « a » et « b » étant des nombres positifs.		,

Remarque : Ce qui est vrai pour deux facteurs l’est aussi pour plus de deux facteurs.
1^ère application : or donc qui s’écrit : On dit que l’on a « fait sortir « 2 » du radical » . = = = , On a fait sortir « 5 » du radical . « » et « » étant des nombres positifs. =
Activité 1 :



2^ème application :
= peut s’écrire =
=		=
= = = =
Autre méthode : = =

Activité 2 : Simplifiez l’écriture de : (faites sortir le plus grand entier possible du radical.)


3^ème application :
; on a « fait entrer « 5 » sous le radical ».
« » et « » étant des nombres positifs. =
Activité 3 : Faîtes entrer sous le radical les nombres qui n’y sont pas.



4^ème application :


D’une manière générale ,	« » étant un nombre positif et « » un entier naturel
= = = = =


	Fiche 8 : Racine carrée d’un quotient.			Info ++@ ++++
	= = ; . Vous constatez que « a et « b » étant des nombres positifs ( « b » non nul ). , , existent et sont positifs. Nous allons démontrer que . Pour cela , calculons : et ; = = ; donc
	Théorème : « a et « b » étant des nombres positifs ( « b » non nul ).
	Activités :





	Activité : exercices S1 : Simplifiez l’écriture des nombres suivants :


	Activité : exercices S2 : Simplifiez les produits suivants : (faîtes sortir des facteurs des radicaux de telle sorte que les radicaux soient des entiers les plus petits possibles ) .


	Fiche 9 : Somme algébrique où figure des radicaux.

				Vous constatez que

	Attention : « a et « b » étant des nombres positifs , en général ,
	Il est malgré tout possible de simplifier certaines sommes où figurent des radicaux.



	Activités (exercices S3) : Simplifiez de même


Fiche 10 : Résolution d’équations et de problèmes.
Exemple : Résolvez l’équation « » d’inconnue « ». En transposant on obtient : « » et après simplification il reste : « » .soit « » L’équation est de la forme « ax + b = 0 » dans laquelle « a = 7 » et « b = » Elle possède une solution unique :
Exercice 1 : Résolvez l’équation « » d’inconnue « ».

Exercice 2 : Résolvez les équations ci-dessous d’inconnues respectives « x » , « y », « z » , « t »
	Equations.		Voir le produit en croix……
	Intermédiaires.	« x² = 144 »
	Solutions.	12

Problème 1 . Un rectangle est tel que sa longueur est le double de sa largeur. Calculez ses dimensions sachant que son aire est « 3528 cm² »

Problème 1 . Un disque a pour rayon « 1m ». Quelle est la longueur du côté du carré ayant la même aire que le disque ? Donnez la valeur exacte puis une valeur décimale approchée à 10^-3 près .

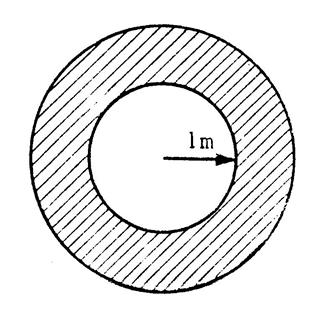
Problème 1 . La couronne ci-contre ( hachurée) est limitée par deux cercles concentriques. Le rayon du cercle intérieur est « 1m ». Quel doit-être le rayon du cercle extérieur pour que l’aire de la couronne soit égale à l’aire du disque intérieur ? Donnez la valeur exacte puis une valeur décimale approchée à 10^-3 près .


Fiche 11 : Exploitation de données statistiques. Elle est complémentaire ( ce niveau on vous demande de faire l’étude sur les statistiques.)
Voici ci-dessous la liste des tailles (en cm ) de 54 élèves de troisième.
159	168	157	164	149	152	172	161	158	145	165	159	163	174	155		166		167		149
160	159	177	169	161	154	156	172	160	162	158	147	168	163	167		145		156		161
164	151	168	178	156	153	162	156	154	161	154	156	170	164	164		152		157		165

En vous souvenant de ce que vous avez vu et étudié dans le classe précédente , remplissez le tableau ci-dessous ( donnez les pourcentages à 0,01 prés) Remarquez que l’on a constitué 7 tranches de tailles ( la lettre « t » désigne la taille )																	Info 4^ème

Tranches de tailles .				« t < 150 »		150 t < 155		155 t < 160		160 t < 165		165 t < 170			170 t < 175				« t 175 »
Effectifs
Effectifs cumulés
Fréquences en %
Fréquence cumulée.
Angles

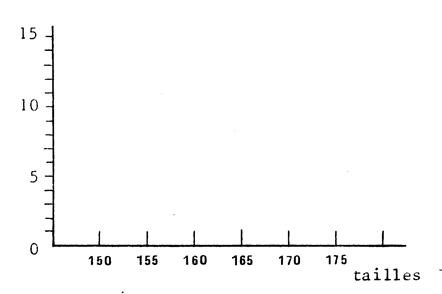
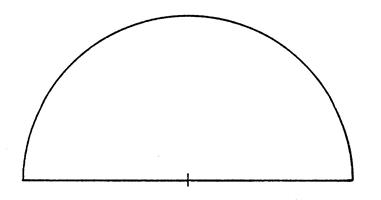
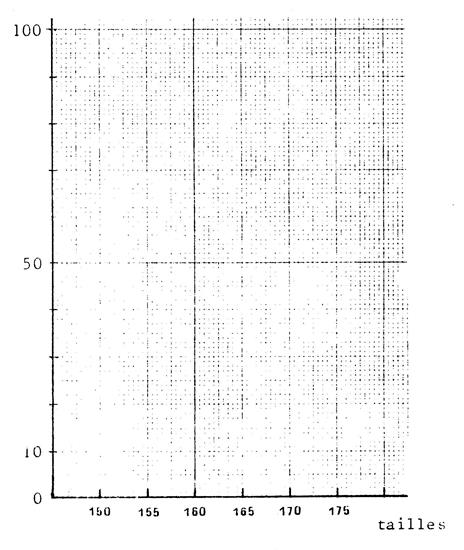
1. Faîtes l’histogramme des effectifs. 2. Faîtes le diagramme semi-circulaire des fréquences ( remplissez la ligne « angles ») 3. Faîtes le diagramme en bâtons des fréquences cumulées. Et tracez le polygone des fréquences cumulées.

Effectifs :

Fréquences.

Fréquences cumulées ( en %)

En utilisant le diagramme qui convient le mieux, répondez aux questions suivantes : Quelle est la tranche de tailles la plus fréquente ?. Quel est le pourcentage d’élèves qui mesurent moins de 157 cm ? Quel est le pourcentage d’élèves qui mesurent au moins de 168 cm ? Quelle est la taille ( à 1 cm près) pour laquelle il y a autant de tailles en dessous que en dessus ? ……. ; cette valeur est appelée « médiane ».

Fini le 1/02/2025

TRAVAUX AUTO FORMATIFS.

CONTROLE

Partie 1

1°) Dites tout ce que vous savez sur ce symbole:

2°) Que désigne le mot « radical » ?

3°) Que désigne le mot « radicande » ?

Partie 2 : LES RACINES CARREES.

4°) Donner les trois écritures utilisées en mathématique pour indiquer que l’on désire connaître la valeur de la racine carrée d’un nombre.(prenez le nombre : 36 )

*on ne vous demande pas de faire le calcul !

5°) Traduire en langage littéral , donner son utilisation :

"ixe" puissance un sur i grec

traduire :

: est égale est égale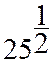

6°) Que cherche - t - on à obtenir lorsque l’on veut connaître la racine carrée d’un nombre ?

7°) Quelles sont les différentes façons de connaître la racine carré d’un nombre ?

*cela sera vraie pour tous les cas de recherche de la valeur des « racines ».

8°) Donnez la procédure permettant d’obtenir la racine carrée d’un nombre à la calculatrice!

(Il en existe deux .......).

9°) sous la racine il y a des nombres séparer par des signes opératoires ; que faut –il faire avant de rechercher la racine ?

10°) Sous la racine on a une inconnue , il faudra donc « résoudre » , comment faudra t –il procéder pour isoler ?

EVALUATION

1° ) Trouver les racines carrées parfaits des multiples de dixLavec la calculatrice)

de 10⁰ à 10 ⁸

si elles existent ! pour 10⁰ ;10¹; 10²; 10³ ; 10⁴ ; 10⁵ ; 10⁶ ;10 ⁷ ; 10^8;

2°) soit un nombre « x » ; trouver la racine carrée du nombre :

x =0,25 ; =

x = 7,29 ; =

x = 33,64 ; =

x = 81 ; =

x = 291 600 ; =

x = 2 744 000 ; =

x = 1,574610⁸ ; =

3 ° ) Faire les calculs suivants à l’aide d’une calculatrice ;donner le résultat avec la précision du dixième

4 ° ) Faire les calculs suivants à l’aide d’une calculatrice ;donner le résultat avec la précision du centième

(faire d’abord le calcul sous le radical ) =

5 °) Faire les calculs suivants à l’aide d’une calculatrice ;donner le résultat avec la précision du millième ((faire d’abord le calcul sous le radical)