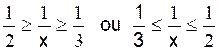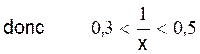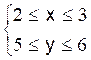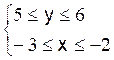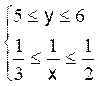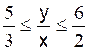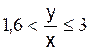Pré requis:

Valeur approchée  et approximation
La division décimale

ENVIRONNEMENT du dossier:

Index    warmaths

Objectif précédent   1° ) nombre décimal 2°) nombre rationnel 3°) Arrondir  et troncature ; 4°) Ordre de grandeur

INFO   : 1°) Info            2°) valeurs approchées et encadrement(BEP) 3°) encadrement d’une racine 4°)puissance « encadrement »

Tableau synoptique          Liste des cours sur le calcul numérique

     « ENCADREMENT »

 

1°) Encadrer un nombre 

2°)   Encadrement d’un résultat :  (classe 6ème )

3°) Encadrement du résultat de la division euclidienne et le quotient non exact :

4°) encadrement  et  « irrationnel » ( exemple : racine carré )

5°) Encadrement  d’un rationnel  et division d’un rationnel

Voir encadrement : d’une puissance (hors cours)

6°) Encadrement d’opérations simples

7°) Encadrement : application à un problème simple.

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

COURS

 

Les encadrements sont des doubles inégalités ; Ils ont les mêmes propriétés que les inégalités simples : addition membre à  membre  des encadrements  de même sens…….

Mais , comme pour les inégalités simples , on n’ a pas le droit de les soustraire ni de les diviser . Lorsque l’on veut encadrer une différence «  a - b » , on commence par encadrer (-b)  puis la somme  « a + (-b) , c’est à dire « a - b »

 

De même, pour  encadrer un quotient   , on encadre  puis le produit   , c’est à dire  

D’un encadrement, on peut déduire un autre encadrement en agrandissant celui de départ, jamais en le diminuant.

 

 

 

1°) Encadrer un nombre :

Encadrer un nombre c’est le placer  entre un nombre plus petit que lui  et un autre plus grand que lui .

Exemple :   7 < 7,6 < 8

On dit que 7 est la valeur entière approchée par défaut ; 8 est la  valeur entière approchée par excès.

 

On peut encadrer par deux nombres entiers , ou deux nombres  entiers successifs .

Exemples:

-par deux entiers    73 <  89  < 134

 

73 est plus petit que 89 ;  134 est plus grand que 89

 

- par deux entiers successifs :      88< 89 <90

 

88 est immédiatement plus petit que 89 ; 90  est immédiatement plus grand que 90

 

On peut encadrer par deux nombres décimaux ; par deux nombres décimaux successifs qui n’ont qu’un chiffre après la virgule .

 6,7 < 6,78 < 6,8

 

On dit que 6,7 est la valeur entière approchée à un dixième par défaut ; 6,8 est la  valeur entière approchée à un dixième par excès.

 

 

On peut encadrer par deux nombres décimaux successifs  qui n’ont deux chiffres après la virgule.

 

Exemple : donner la valeur approchée de  3, 872 9 au centième près .

 

Pour le centième près , on prend deux chiffres après la virgule .

                     3 , 87 <  3, 872 9  < 3,88

 

3,87 est la valeur approchée au centième près par défaut ; 3,88 est la valeur approchée au centième près par excès.

 

2°)   Encadrement d’un résultat :  (classe 6^ème )

 

Un résultat décimal  est toujours compris entre deux nombres entiers ou deux nombres décimaux .

Nous pouvons donner des encadrements de résultats :

 

Exemples :   0 <  0,63 < 1

                0,6 < 0,63 < 0,7

                0,62 < 0,63 < 0,64

 

3°) Encadrement du résultat de la division euclidienne et le quotient non exact :

Utilité   de l’encadrement du dividende sous la forme :

     

                                           b    q <   a  < b ( q + 1)

 

 

  (utiliser  pour  approcher un nombre dans  les tables de multiplication ) ; en vue de trouver  la valeur du diviseur  en se posant la question :« combien de fois y  a t - il.... « tel nombre »......dans....« tel nombre ».... ? »

 

 

exemple : combien y a t il de fois « 6 » dans « 27 » ?

 D ‘après la table des multiplications  ( fois 6 )   6 fois 5 = 30 ; 6 fois 4 = 24»

 

donc  dans la table  des « 6 » ; 27 est compris entre  24 et 30

 

ce qui se traduit :                                                24  <  27  <  30

 

soit                                                                64. <   27   < 6 5   

      

on retrouve  la forme

 

 

Nous obtenons avec cette relation d’encadrement

 

4°) encadrement  et  « irrationnel » ( exemple : racine carré )et ( Info plus sur les encadrements de racines)

 

a)   Valeur approchée  et encadrement   d’une racine carrée

Pré requis : arrondir et troncature

Sur la calculatrice , on lit = 2,236 067 978 ….

En général il est inutile de donner toutes les décimales.

Mais on peut affirmer par exemple que :  2,236 <   < 2,237

 

On dit que l’on a un encadrement de  d’amplitude 0,001 .

 

2,236 est une valeur approchée par défaut à  10^-3 prés (par excès)de   

 

2,237 est une valeur approchée par excès à  10^-3 prés  (par défaut)de

 

 

Plus généralement :

 

Si  a - 10^-n  £  x  £   a + 10^-n 

On dit que « a » est une valeur approchée de « x » à la précision : 10^-n

 

Autres exemples :

 

Encadrement d’amplitude 10-4 de	Calculatrice :   = 44,69899328 donc  44,6989£  £  44,6990
Encadrement d’amplitude 10-4 de	Calculatrice :  = 0,234520788 donc : 0,2345£  £  0,2346

 

5°) Encadrement et division d’un rationnel

 

Exemple :  x =           

 

 

 

17 , 000000      44   3   80              280                      0,38 63 63 63 …             0,386363  < x < 0,386364                                                             160            280               période  « 63 »              160                ….        0,386363   est la valeur approchée à 10-6 prés par défaut de « x »      0,386364 est la valeur approchée à     10-6 prés par excès de « x »    d’où l ‘encadrement du résultat de la division :                            0,386363  <  < 0,386364

 

6°) encadrement  d’opérations : de nombres « encadrés »  ( niveau seconde)

 

Application : Deux nombres « x » et « y » vérifient       2 £  x £  3     et  5 £  y £  6   

 

 On veut en déduire un encadrement des nombres suivants par des nombres décimaux ayant au plus un chiffre après la virgule :

 

x²

- x

x + y

;  x y

y - x

 

2 £  x £  3      et   5 £  y £  6   

 

		Réponses :
x²	2 ; x et 3 sont positif	4£  x² £  9
	£   £    or   1,4  <  et    < 1,8	donc        1,4 £   £  1,8
-x	- 2  ³ - x   ³ - 3	Donc    - 3 £ - x £ - 2
	2 ; x et 3 sont non nuls et de même signe	or 1/2 = 0,5   et 1/ 3 = 0,3
x+ y		Donc :  (2+5) £  x + y £ (3+6)      7 £  x + y £   9
x y		2 ;x ; 3 ; 5 ; y ; 6 étant positifs.          10 £ x y £ 18
y - x		Donc 2    £ y - x  £   4
		Les six membres étant positifs       or 5 / 3 >  1 , 6  et  6/2 = 3   donc :

 

 

7°) Problème d’application :

 

Une unité de longueur  étant fixée , soit P le périmètre d’un rectangle de côtés l et L.

1°) Exprimer  « P » en fonction de « l » et  « L » ; en déduire l =  P/ 2 - L

2°) On sait que   L vaut 3,2 à 0,1 près et que P vaut 8,4 à 0,1 prés.

a)    Ecrire  un encadrement de L et un encadrement de P

b)   Déterminer alors un encadrement de « l » par des nombres décimaux  n’ayant qu’un seul chiffre après la virgule.

 

Solution :

1°) On a  P = 2 l + 2 L = 2 ( l + L) , il en résulte  que

si         P = 2 ( l +L)  alors    P/ 2 = L + l     soit   P/2 - L = l

  donc                                     l = P/2 - L

 

2°) a) la phrase «  L vaut  3,2 à 0,1 prés » signifie :    3,2 - 0,1 £  L £  3,2 + 0,1

 

c’est à dire :     3,1 £  L £  3,3

 

de même on a :  8,4 - 0,1 £  P  £  8,4 + 0,1  soit      8, 3  £  P  £  8,5

 

c)    comme  l = P/2 - L  , encadrons successivement  P/2 ; - L ; P/2 + (-L)

 

On a    8, 3  £  P  £  8,5  donc  4,15  £  P  £  4,25           ( 1)

 

 3,1 £  L £  3,3    donc     - 3,1 ³  -  L  ³ -  3,3    c’est à dire :   - 3,3 £  - L £  -  3,1  (2)

 

On additionne  membre à membre  les encadrements  ( 1) et (2)

 

                                    4,15 + ( -3,3)   £  P/2 + ( -L) £  4,25  + ( -3,1)

                                                               0, 85  £  l  £ 1,15

 

Cet encadrement de « l » ne répond pas à la question , les nombres 0,85 et 1,15 ayant deux chiffres après la virgule.

Mais on a :   0,8 < 0,85  et  1,15 < 1,2  d’où  

             

 0,8 < 0,85  £    l    £   1,15 < 1,2 

 

et par suite  0,8 < l < 1,2  , encadrement de « l » qui répond à la question.

 

 

 

 

 

 

Travaux auto formatifs.

 

CONTROLE :Préparation

1 )Que veut dire « encadrement »  ?

Voir dictionnaire

 

 

 

EVALUATION à préparer

 

 

 1°)  Définissez le rationnel suivant , à partir de son développement

 

 2°) Deux nombres « x » et « y » vérifient       2 £  x £  3     et  5 £  y £  6   

 On veut en déduire un encadrement des nombres suivants par des nombres décimaux ayant au plus un chiffre après la virgule :

 

x²

- x

x + y

;  x y

y - x

 

Problème d’application :

 

Une unité de longueur  étant fixée , soit P le périmètre d’un rectangle de côtés l et L.

1°) Exprimer  « P » en fonction de « l » et  « L » ; en déduire l =  P/ 2 - L

2°) On sait que   L vaut 3,2 à 0,1 près et que P vaut 8,4 à 0,1 prés.

d)   Ecrire  un encadrement de L et un encadrement de P

e)    Déterminer alors un encadrement de « l » par des nombres décimaux  n’ayant qu’un seul chiffre après la virgule.