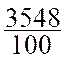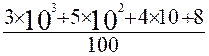Pré requis:

Lecture :1 les nombres rationnels

Lecture 2 : les nombres irrationnels

Valeur approchée et approximation

Approximation et les nombres rationnels et irrationnels

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent 1°) arrondir et troncature 2°) le nombre décimal 3°) encadrement et valeur approchée ( ) 4°) Fiche activités collège ( 6^ème )

INFO sur les nombres décimaux Ordre de grandeur Ordre de grandeur d’un résultat.

Tableau :BEP Liste des cours en relation avec le calcul numérique

DOSSIER :VALEUR APPROCHEE 

1. Valeur approchée d’un « irrationnel » et approximation décimale , d’ordre « n » , par défaut et par excès de «  a »

2. Valeur approchée « rationnel » et « irrationnel »

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Rappel 1 : décomposition d’un nombre entier par ordre :

3548 = 3000 + 500 + 40 + 8

ce qui peut s’écrire :

3548 = 310³ +510² + 410¹ + 8

Rappel 2 : nombre décimal et virgule

Un nombre rationnel représenté par une fraction décimale peut s’écrire sous forme de nombre décimal :

a = =

a = 310 + 5 + +

a = 30 + 5 + 4 10^-1 + 8 10^-2

avec «  la convention de la virgule » entre le chiffre des unités et le terme en 10^{-1 ,} on obtient l’écriture commode : a = 35 , 48

1°) Valeur décimale approchée d’un nombre rationnel

Ou comment remplacer un nombre rationnel qui n’est pas une fraction décimale , par des valeurs approchées

On appelle « valeurs approchées » à près d’une fraction positive deux nombres et tels que :

£ £ ; avec p Î N et n Î N

On dit que est la valeur approchée de à près par défaut .

Remarque :

le sinus , cosinus et tangente d’un angle sont des rationnels , ce sont nombres décimaux « arrondis » , ce sont des valeurs« approchées ». ces nombres sont obtenus en effectuant une division de deux longueurs .

2) Encadrement d’un irrationnel

Soit « x » un nombre entier relatif .

x 10^-n £ a £ (x + 1) 10^-n est un encadrement de  « a » par deux entiers consécutifs multipliés par une même puissance de 10 .

L’amplitude de cet encadrement est 10^{-n .}

x 10^-n est l’approximation décimale , d’ordre « n » , par défaut de « a »

(x + 1) 10^-n est l’approximation décimale , d’ordre « n » , par excès de « a » .

Exemple :

2,236 £ £ 2,237 ; on l’écrit aussi :

2236 10^-3 £ £ 2237 10^-3

2,236 est l’approximation décimale , d’ordre « 3 » , par défaut de

2,237  est l’approximation décimale , d’ordre « 3 » , par excès

Travaux auto formatifs

CONTROLE :Préparation

1 ) Que veut dire approximation" ?

Voir dictionnaire

2 ) Qu'est ce qu'une valeur arrondie?

3 ) Qu‘est ce qu‘une troncature ?

4 ) En vous aidant du nombre suivant........... 61, 91683..................répondez aux questions suivantes :

5 ) Donner la procédure qui permet de faire une troncature.

6 ) Donner la procédure qui permet d ‘ arrondir par excès.

7 ) Donner la procédure qui permet d ‘ arrondir par défaut.

8 ) Donner la procédure qui permet d ‘ arrondir   à « tant »près  .

9 ) Combien y a t - il de façon de rendre compte d’un résultat d ’ une opération (division ou « racine ».

EVALUATION à préparer

Tableau 1 :

ARRONDIR	à :.....0,1.............	à ...0 ,01	à 0 , 001
Nombres	troncature	par excès	par défaut	au 0,01 près
61, 91683
61,95862
61, 96568
61,99231

Tableau 2 :

ARRONDIR	à 1 près	à 0,1 près	à 0, 01 près	0,001 près
61, 91683
61,95862
61, 96568
61,99231

2°) Les valeurs approchées par défaut d’un nombre sont successivement : 1 ; 1,1 ; 1,12 ; 1,12123 ; 1,121231234, etc . ;les chiffres décimaux successifs constituant une suite de plus en plus longue des nombres entiers .Le nombre est-il rationnel ? est-il réel ?