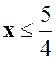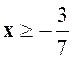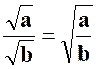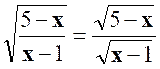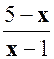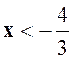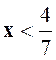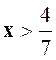|
|
|
|
|
|
|
Le "carrée"
parfait |
ENVIRONNEMENT du dossier:
|
|
1°)Racines carrés d’opérations simples |
2°) liste des objectifs sur les puissances et racines |
|
|
|
|||
|
|
|||
|
|
|
|
|
DOSSIER:
LES radicaux carrés : La racine carrée d’une expression algébrique.
|
|
1°) Racine carré d’une expression algébrique . |
|
|||||
|
|
2°) Application des propriétés
. |
|
|||||
|
|
3°) Racines carrée d’un carré parfait algébrique. |
|
|||||
|
|
4° ) Donner les divers
expressions rationnelles |
|
|||||
|
|
|
|
|
|
|
|
|
|
COURS |
Interdisciplinarité |
|
|||||
|
|
|
|
|
|
|
||
|
Travaux avec la
calculatrice : taper des
valeurs et comparer le résultat donné
par la table numérique |
|
|
|
COURS. |
|
|||||||||||||
|
|
1°) Racine carré d’une expression algébrique . |
|
|||||||||||||
|
|
« les nombres négatifs n’ont pas de racine carrée » Si donc on a une écriture tel que : Si bien que ces questions sont tributaires de la théorie des inéquations,
à l’occasion de laquelle elles seront développées. Mais nous pouvons donner quelques premiers exemples simples. |
|
|||||||||||||
|
|
Exercices : |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
1 : |
|
|||||||||||||
|
|
· Pour
quelles valeurs de « x »
l’expression : |
|
|||||||||||||
|
|
Solution : |
|
|||||||||||||
|
|
Les mots : « avoir un sens » ; « être
défini » ; « exister » ont la même signification |
|
|||||||||||||
|
|
Possibilité du calcul de l’expression dés
que la valeur numérique de « x » est fixée. L’expression n’existe que pour :
|
|
|||||||||||||
|
|
|
2x + 3 2 x x |
|
||||||||||||
|
|
Exercices
2 : |
|
|||||||||||||
|
|
· Pour
quelle valeur de « x » l’expression |
|
|||||||||||||
|
|
Indication : Ecrire 5 – 4
x |
|
|||||||||||||
|
|
Réponse : |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
3 : |
|
|||||||||||||
|
|
· Pour
quelles valeurs de « x » l’expression |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Réponse : |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
2°) Application des propriétés
. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
L’application des propriétés Ces égalités , vraies pour des nombres, ne le
sont pas d’emblée pour des expressions algébriques. Ecrire : En effet, le premier membre de (1) exige que |
|
|||||||||||||
|
|
|
Ou bien négatifs : x
< 1 ; x < 2 donc en bloc « x < 1 » Ou bien positifs :
x > 1 ; x > 2 donc en bloc « x > 2 » |
|
||||||||||||
|
|
Le premier membre existe donc : soit pour « x < 1 » et soit pour
« x > 2. Mais le second membre exige que « x – 1 » et « x – 2 » soient séparément et
simultanément positifs ;Donc « x >
2 » L’égalité ( 1 ) n’est donc correcte que pour
« x > 2 » |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
4 : |
|
|||||||||||||
|
|
· Pour
quelles valeurs de « x » peut-on écrire : |
|
|||||||||||||
|
|
Solution. Le premier membre exige : |
|
|||||||||||||
|
|
|
3 – x > 0 ou x < 3 x – 2 > 0 ou
« x > 2 |
Donc : 2 < x < 3 |
|
|||||||||||
|
|
Le second membre exige :
( 3 – x ) ( x – 2 ) > 0 |
|
|||||||||||||
|
|
Donc, ou bien |
|
|
|
|
|
|||||||||
|
|
|
3 – x < 0 x – 2 < 0 |
Ou x > 3 Ou x < 2 |
incompatibles |
|
|
|||||||||
|
Ou bine |
|
|
|
|
|||||||||||
|
|
3 – x > 0 x – 2 > 0 |
Ou x < 3 Ou x > 2 |
Donc : 2 < x < 3 |
|
|||||||||||
|
|
L’égalité écrite est valable pour toutes les valeurs de
« x » comprises entre « 2 » et « 3 » Les domaines d’existence des deux membres sont les mêmes.. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
5 : |
|
|||||||||||||
|
|
· Pour
quelles valeurs de « x » peut-on écrire : |
|
|||||||||||||
|
|
Indication : Il faut étudier les signes de « 5 – x » ; de « x-1 » et de Réponse : Egalité valable pour « 1 < x < 5 » |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
6 : |
|
|||||||||||||
|
|
· Pour
quelle valeur de « x » a – t- on : |
|
|||||||||||||
|
|
Réponse : Le premier membre exigeant : « x <
2 » et « x > 3 » |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
3°) Racines carrée d’un carré parfait algébrique. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Il y a lieu de ne jamais oublier que le symbole « Si donc à l’occasion de « |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
De telle sort que chaque cas le résultat final soit positif. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
7 : « Transformer » |
|
|||||||||||||
|
|
· |
|
|||||||||||||
|
|
Réponse : |
|
|||||||||||||
|
|
|
E = 2 x – 3 , si 2x – 3 > 0 ou
|
|
||||||||||||
|
|
|
E = 2 x – 3 , si 2x – 3 < 0
ou |
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
8 : « Transformer » |
|
|||||||||||||
|
|
· |
|
|||||||||||||
|
|
Réponse : |
|
|
||||||||||||
|
|
|
E = 3 x +4 , si 3x + 4
> 0 ou |
|
||||||||||||
|
|
E = - 3 x - 4 , si
3 x + 4 <
0 ou |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
9 : « Transformer » |
|
|||||||||||||
|
|
· |
|
|||||||||||||
|
|
Réponse : |
|
|
||||||||||||
|
|
E = 4 – 7 x pour : E = 7 x – 4 pour |
||||||||||||||
|
|
|
||||||||||||||
|
|
Exercices
10 : Donner
les divers expressions rationnelles de : |
|
|||||||||||||
|
|
E = |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
x – 5 pour
x > 5 5 – x pour
x < 5 |
|
||||||||||||
|
De même |
|
||||||||||||||
|
|
x + 7 pour
x > - 7 - x – 7 pour
x < - 7 |
||||||||||||||
|
|
|
|
|||||||||||||
|
|
Il faut donc envisager les intervalles : ( - |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Intervalle 1 :
- |
|
|||||||||||||
|
|
Intervalle 2 :
- 7 < x < 5
; E 2 =
x + 7 + 5 – x = 1 2 |
|
|||||||||||||
|
|
Intervalle 3 : 5 < x
< + |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
11 Donner les divers expressions rationnelles de |
|
|||||||||||||
|
|
E
= |
|
|||||||||||||
|
|
Indications :
Donner les expressions de |
|
|||||||||||||
|
|
|
- |
|
||||||||||||
|
|
|
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
Exercices
12. Quelle sont ,
suivant les valeurs de « x », les expressions rationnelles
de : |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Réponses : |
|
|||||||||||||
|
|
|
- |
|
||||||||||||
|
|
|
2 < x < + |
|
||||||||||||
|
|
|
|
|||||||||||||
TRAVAUX AUTO FORMATIFS.
EVALUATION refaire les exercices du cours…….