|
Auteur :
WARME R.
INFORMATIONS sur
|
|||||||||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|||||||
|
Année scolaire : ……………………… |
Dossier pris
le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|||||||
|
ETABLISSEMENT :
………………………………………….. |
|||||||||
|
Titre |
|||||||||
|
N°18 |
LES POLYGONES
USUELS |
||||||||
|
CHAPITRES |
||||||||
|
|
INFO
Cd ++++ |
|||||||
|
|||||||||
|
|||||||||
|
Cd :Info plus :
Aire des polygones 1!! Cd :Info 2 : liste des calculs
d’aire des surfaces élémentaires. |
||||||||
|
Dictionnaire : voir définition du mot : « usuel » |
||||||||
|
COURS |
||||||||
|
i Nous
étudions dans ce cours les polygones réguliers usuels . Ils sont
au nombre de 8 . Le
triangle rectangle fera l'objet d'une étude plus approfondie ( il
possède des caractéristiques particulières qui seront utilisées
lorsque l'on étudiera " Pythagore"
et " les
relations trigonométriques" ). |
||||||||
|
|||||||||
|
a) Définition : Un
polygone est une portion de plan limitée par une ligne brisée fermée. Un polygone est donc une
figure géométrique plane construite avec des traits rectilignes ( segments) . b) liste des
polygones usuels . Le triangle isocèle , le triangle équilatéral , le triangle rectangle , le trapèze , le
parallélogramme , le losange , le rectangle , le carré . Il existe les polygones dits " réguliers" et "irréguliers" . =par définition : - Un polygone est dit « régulier »
lorsque tous ses cotés sont égaux ainsi que
tous ses angles . - Un polygone est dit
« irrégulier » lorsqu ‘un de ses cotés n’est pas égal aux
autres ainsi qu ‘un de ses angles soit d’ une valeur différente des autres
ses angles . =Les polygones usuels réguliers sont : le triangle
équilatéral et le carré =Les polygones usuels irréguliers sont : le triangle isocèle , le triangle rectangle , le trapèze , le
losange , le rectangle . tous les
parallélogrammes (exclu :le carré ) ; i
Les 5 principaux polygones
réguliers sont : |
||||||||
|
1)
Le
triangle équilatéral |
|||||||||
|
2)
Le
carré |
|||||||||
|
4)
L’hexagone
régulier |
|||||||||
|
( info CD : parmi
leurs caractéristiques ils
possèdent des axes de symétrie). |
|||||||||
|
II
) PROPRIETES
DES POLYGONES USUELS. |
||||||||
|
C.D. voir : INFO plus liste des polygones !!) i pour en
savoir plus sur les propriétés et les caractéristiques des figures , cliquer
sur Cd :info plus . |
||||||||
|
Description |
Propriétés. |
Cd i |
|||||||
|
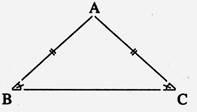
Triangle
isocèle (ACB)
|
-
Deux côtés de même longueur : [ A B] et [AC] -
Deux angles de même mesure : -
Un axe de symétrie : la médiatrice du coté [BC] |
||||||||
|
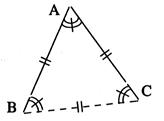
Triangle équilatéral (ACB) |
-
trois côtés de même longueur: [ A B] , [AC]
et [B C] -
Trois angles égaux : -
Trois axes de
symétrie .ce sont les supports des
trois médiatrices des côtés. |
||||||||
|
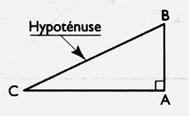
Triangle
rectangle .(BAC)
|
- possède un angle droit .le milieu de l'hypoténuse est le centre du
cercle circonscrit.(point de convergence des médiatrices ) . |
||||||||
|
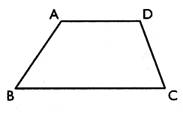
|
-
deux côtés parallèles : [ A D] , [BC] -
deux côtés non parallèles : [ A B] , [DC] |
||||||||
|
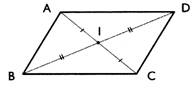
Parallélogramme : ( ADCB)
|
-
Côtés sont parallèles et égaux deux à deux . -
Les diagonales se coupent en leur milieu . - Dans un parallélogramme les angles opposés
sont égaux. |
||||||||||
|
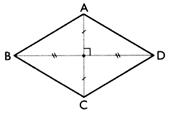
Losange : ( ADCB)
|
-
Côtés parallèles deux à deux et de même longueur. AD =
DC =C B = BA - Les diagonales sont perpendiculaires : [
A C] , [BD] . |
||||||||||
|
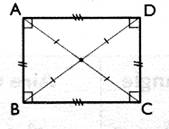
Rectangle (ADCB)
|
-
parallélogramme ayant quatre angles droits. -
Les diagonales sont de même longueur . |
||||||||||
|
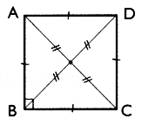
Carré
: ( ADCB)
|
-
parallélogramme ayant quatre angles droits et dont les
diagonales , de même longueur , sont perpendiculaires. -
Rectangle dont deux côtés consécutifs ont même longueur . -
Losange ayant un angle droit . |
||||||||||
|
|
||||||||||
|
|
|
|||||||||
|
Intitulés ( désignations) |
Formules |
Cd :Info plus |
|||||||||
|
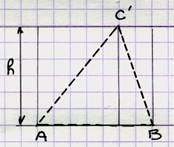
Aire du triangle quelconque ( scalène): |
Aire = Ou Aire = b : longueur de la base. h : longueur de la hauteur. |
||||||||||
|
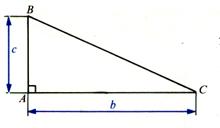
Aire du triangle rectangle : |
Aire = |
||||||||||
|
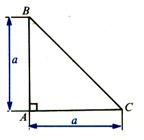
Aire du triangle isocèle
:
|
Aire = |
||||||||||
|
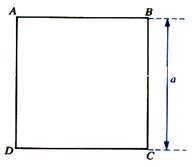
Aire du carré : Si
"a" est la mesure du côté . |
Aire : A = a² Avec
"a" : longueur du
côté |
||||||||||
|
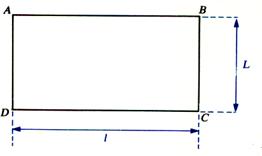
Aire du rectangle :
|
Aire : A = L L : longueur l :
largeur |
||||||||||
|
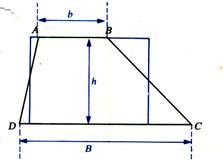
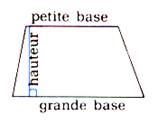
Aire du trapèze :
|
Aire : A = B : longueur de la grande base. b: longueur de la
petite base. h : hauteur |
||||||||||
|
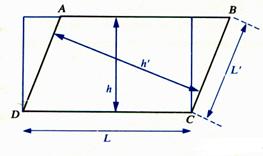
Aire du parallélogramme :
|
Aire : A = L L : longueur h :
hauteur ou A = L' |
||||||||||
|
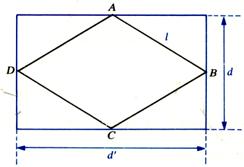
Aire du losange :
|
Aire : A = d ' : grande
diagonale. d : petite diagonale . |
||||||||||
|
Attention !!!: pour les calculs les unités de
longueurs doivent être homogénéisées . ( à savoir
« homogénéisée » : toutes les longueurs doivent
être exprimées dans la même unité, toutes longueurs sont exprimées mm , ou cm , ou dm , m , ou etc. ) |
|||||||||||
|
EXEMPLES DE
CALCULS D’ AIRES : |
|
|||||||||
|
1°) calculer l'aire du triangle avec
b = 20 cm et h = 13 cm. solution : A = 2°) Calculer l'aire du
carré dont la longueur du carré est
de 110 mm. Solution : A = 110 3°) Calculer l'aire du
rectangle dont la longueur est
de 110 mm et la largeur est de 7 cm .
( exprimer le résultat en cm²). Solution : L = 110 mm = 11 cm ; l = 7 cm A = 11 4°) Calculer l'aire du
trapèze dont la grande base est
de 11 cm et la petite base est de 9 cm
et la hauteur est de 6 cm. ( exprimer le résultat en cm²). Solution :
A = |
|
|||||||||