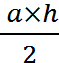Fiche I ) Identifier les figures géométriques. ( nature)

Fiche II ) Evaluation d’aires.

Fiche III ) Aire du parallélogramme.

Fiche IV )  Exercices sur le parallélogramme.

Fiche V )  Aire du losange. 

Fiche VI ) Aire du triangle.

Fiche VII ) Exercices sur le triangle.

Fiche VIII ) Aire du disque.

Fiche IX ) Situations problèmes sur le calcul d’aire.

Interdisciplinarité :

Fiche de travail 

Fiche I ) Identifier les figures géométriques. ( nature)

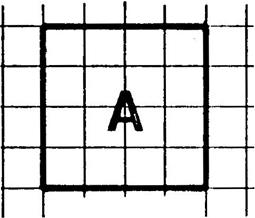
On vous demande de donner la nature  (nom) des figures géométriques ci-dessous.

Ecrire la réponse sous la figure.

Le carré

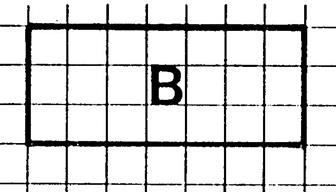
Le rectangle

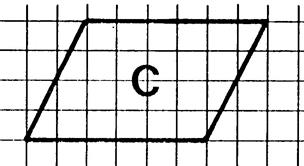
Le parallélogramme

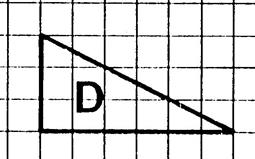
Le triangle rectangle

Le triangle quelconque (scalène)

Triangle isocèle

Le triangle

Losange (carré)

Le trapèze

Le losange

Le rectangle ou parallélogramme.

Fiche II )  Evaluation des aires.

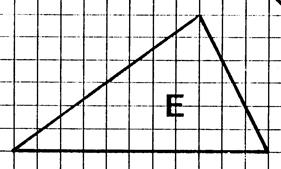
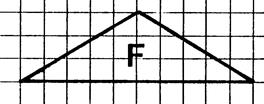
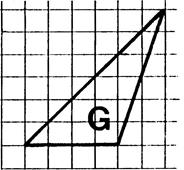
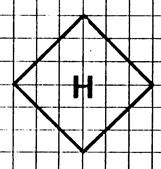
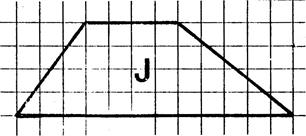
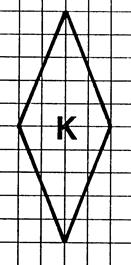
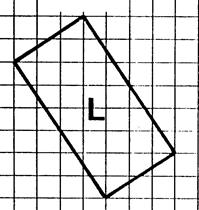
        1°)  En prenant comme « unité d’aire »  , l’aire du carreau du quadrillage déterminez la mesure de l’aire des surfaces représentées ci-dessus.

( vous pouvez vous aider en faisant apparaître des rectangles  ou des moitiés de rectangle.).

2°) Sachant que les carreaux du quadrillage sont des carrés de 5 mm de côté, quelle est en mm² l’aire de ces carreaux ? ( 5 fois 5 = 25 mm²)

3°) Complétez le tableau donnant les aires des surfaces en mm² et cm².

Inscrivez vos résultats dans le tableau ci-dessous.

Aire

surface

A

B

C

D

E

F

G

H

J

K

L

En carreaux

16

21

24

9

33

15

12

18

24

20

28

En mm²

16 fois 25 mm²

En cm²

Fiche III ) Aire du parallélogramme.  ( info plus )

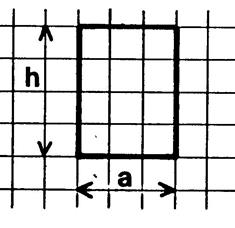
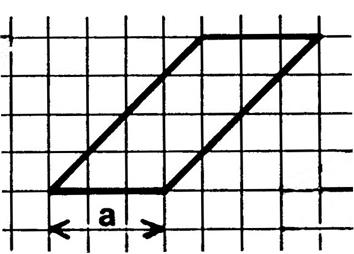
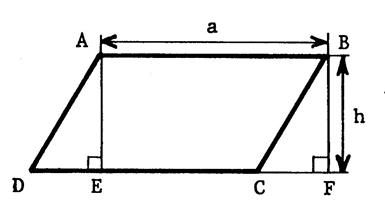
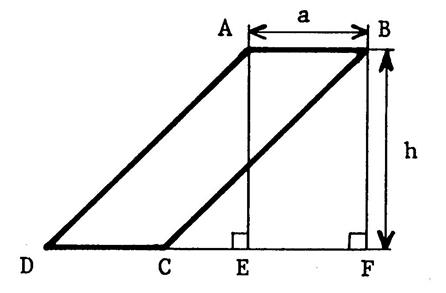
Les parallélogrammes ci-dessous ont tous un côté de longueur « a » et la même hauteur « h ». correspondant à ce côté.

En prenant comme unité d’aire , l’aire du carreau du quadrillage, déterminez l’aire de chacun des parallélogrammes (en comptant les carreaux).

Notez sous chaque figure la mesure de l’aire trouvée.

Valeur  de l’aire  ci-dessus :……12 …………

Valeur  de l’aire  ci-dessus :……12………

Valeur  de l’aire  ci-dessus :……12…………

Valeur  de l’aire  ci-dessus :…………12……

Constat : Vous constatez que ces parallélogrammes ont tous : la même valeur d’aire.

·       Formule donnant l’aire d’un parallélogramme.

Activité :

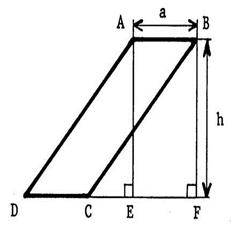
(figure 1 ) Ci-contre : est représenté  un parallélogramme « ABCD ».

·       Tracez la hauteur « AH »

·       Tracez par « B » la perpendiculaire à ( DC).

( elle coupe (DC) en  « F ».

[ BF] est aussi « hauteur » pour le parallélogramme.                                       

On a alors « AE =  BF » ; appelons « h » cette longueur.

Résultat du tracé.

·       « ABFE » est un ……..parallélogramme…..

Appelons « a » la longueur « AB » .

On a aussi « DC = a »   et « EF ..=a »

·       L’aire du rectangle « ABFE » est alors à «  » . 

Découpez le triangle « DAE » et appliquez-le sur le triangle « CBF ».

Observons : Les deux triangles se superposent  ils sont identiques . Donc ils ont la même ..aire..

L’aire du parallélogramme « ABCD » est donc la même que celle du rectangle « ABFE ».

Elle est donc égale à  «  »

Remarque :

Dans le cas de la figure ci-contre, on peut faire le raisonnement suivant :

Evaluons l’aire « ABFD » de deux façons différentes :

-        C’est la somme de l’aire du parallélogramme « ABCD »et de l’aire du triangle « BCF ».

-        C’est la somme de l’aire du rectangle « ABFE » et de l’aire du triangle « AED ».

Comme les triangles « BCF »  et « AED » ont la même aire, alors l’aire du parallélogramme « ABCD » est égale à l’aire du rectangle « ABFE »

A retenir :

L’Aire du parallélogramme ( A)  de côté « a » et de hauteur « h »  est : 

Remarque :

« a » et « h » sont exprimés avec la même unité de longueur et « A » est exprimée avec l’unité d’aire correspondante.

Activité :  Après avoir mesuré « a » et « h » sur la figure 1 , calculez en « mm² » puis en « cm² » l’aire du parallélogramme « ABCD ».

Fiche IV )  Activités ; exercices sur le parallélogramme.

Exercice 1 :Chaque colonne du tableau ci- dessous correspond à un parallélogramme.

Complétez le tableau .

Côté

25 mm

40 m

2,3 cm

Hauteur

15 mm

1,7 m

1,1 cm

Aire

375 mm²

6,8 m²

2,53 cm²

Exercice 2 :

« GHJK » est un parallélogramme.

Les longueurs sont données sur la figue sont en « m »

Calculez la longueur (en « m »)  de la hauteur « h ».

Réponse :

63 fois 30  = 70 fois h

« h » = ( 63 fois 30 ) / 70 = 27 m

Fiche V )  Aire du losange.  ( info. ++résumé) 

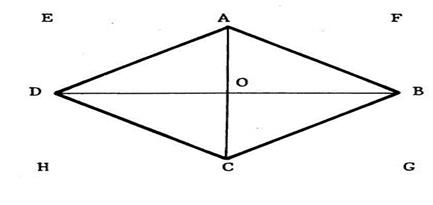
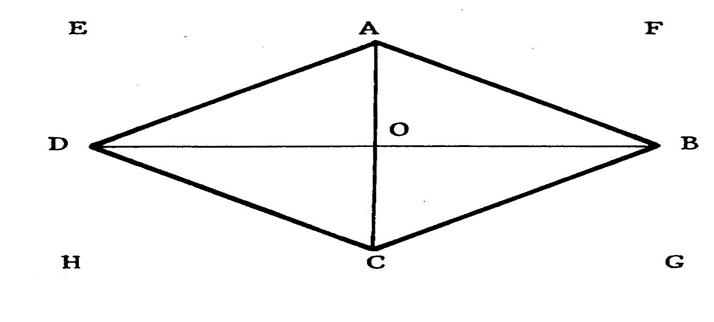
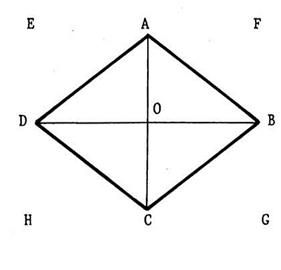
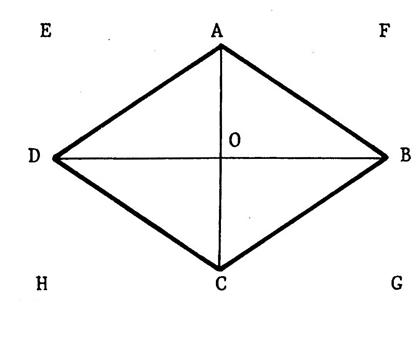
Voir ci - contre un losange « ABCD ».

Nous appelons « a » la longueur de la diagonale [ DB] et « b » la longueur de la diagonale [AC]  .

Vous savez ( voir de 6^ème ) que dans tout losange, les diagonales  sont ….perpendiculaires….

·       Tracez  par  « A » puis par « C » la parallèle à ( DB ) .

·       Puis tracez par « D » puis par « B » la parallèle à  ( AC ).

Ces quatre droites se coupent en des points « E », « F » , « G », « H »,dont le nom est déjà écrit sur la figure.

·       Expliquez (mentalement ou oralement) pourquoi « EFGH » est un rectangle dont les dimensions sont « a » et  « b ».

·       Expliquez (mentalement ou oralement) pourquoi l’aire du losange « ABCD » est la moitié de l’aire du rectangle « EFGH ».

L’aire du rectangle « EFGH » est  égale à : «  » ; l’aire du losange  est alors égale  à  :

A retenir :

l’AIRE du losange  de diagonales « a » et « b »   s’écrit :    

Remarque 1 :

« a » et « b » sont exprimées avec la même unité de longueur  et « A3 est exprimée avec l’unité d’aire correspondante.

Remarque 2 :

Le losange étant un parallélogramme, son aire peut se calculer connaissant la longueur d’un côté et la hauteur correspondante. 

Activité « exercice » :

Exercice 1 :

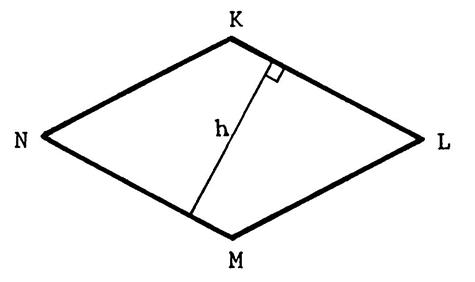
On vous donne ,ci-contre, un losange « KLMN » tel que « NL =  48 mm » et « KM = 36 mm »

Sachant que le côté de ce losange est 30 mm, calculez la hauteur « h ».

Exercice 2 :

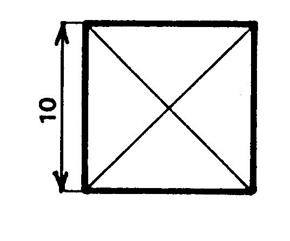
Tout carré est un losange.

Calculez une valeur approchée ( à 1 mm prés)de la diagonale d’un carré de 10 cm de côté.

Vérification : si vous ne savez pas faire le calcul alors faites un dessin à l’échelle 1 , puis mesurez avec une règle la longueur d’une diagonale.

Fiche VI ) Aire du triangle.  ( info +++)

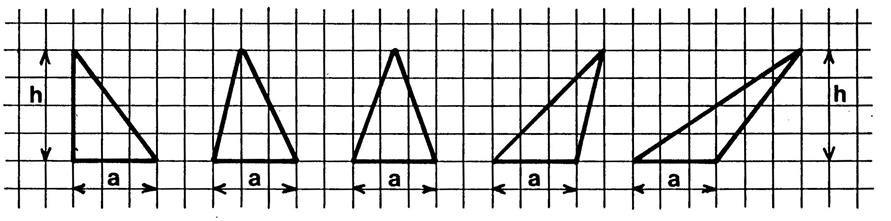
Les triangles ci-dessous ont tous un côté de même longueur « a » et la même hauteur « h » correspondante.

En prenant comme unité d’aire , l’aire du carreau du quadrillage, déterminez  l’aire de chacun des triangles , en comptant les carreaux.

Inscrivez sous chaque figure la mesure de l’aire trouvée.

A=…7 c…

A= 7c

A = 7 c

A = 7 c

A = 7 c

Vous constatez que ces triangles ont tous  la même aire .

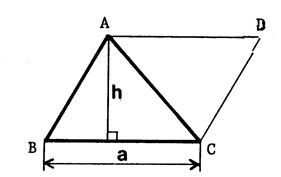
Formule donnant l’aire du triangle.

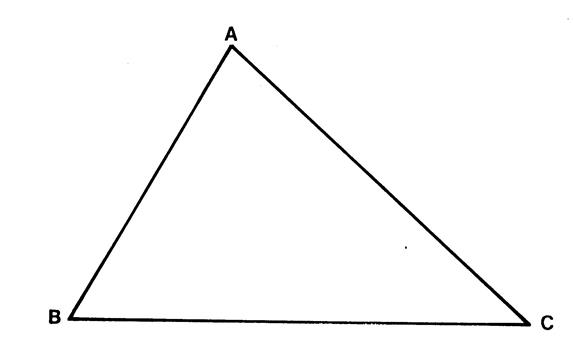
Ci-contre un triangle « ABC ».

A partir de ce triangle, construisez le parallélogramme « ABCD ».

Appelons « a » la longueur « BC » et « h » la hauteur du triangle.

« h » est aussi la hauteur du parallélogramme relative [ BC ].

L’aire du parallélogramme est donc :

·       Découpez la parallélogramme « ABCD » , puis partagez-le en deux suivant la diagonale ( A C ).

Vous obtenez alors 2 triangles « ABC » et « CDA »

Pouvez-vous les faires coïncider ? oui …… Ils ont donc la même mesure d’aire.

Cette aire est donc la « moitié » de l’aire du parallélogramme « ABCD » .C’est à dire      .

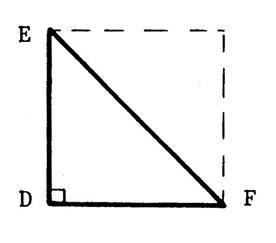
A retenir :

Aire du triangle de côté « a » et de hauteur correspondante « h » est égale à : A =   .

Remarque :

·       « a » et « h » sont exprimées avec la même unité de longueur.

·       Et « A » est exprimée avec l’unité d’aire correspondante.

Exercice : Chaque colonne du tableau ci- dessous correspond à un triangle.

Complétez ce tableau ( attention aux unités).

côté

0,23 dm

…12  mm…= 0,12..dm

15 dm

Hauteur correspondante

0,8 cm

50 mm 

2,2 dm = 0,22.m

Aire

…230 FOIS 80.mm²

6 cm²= 600 mm²

3 300 cm²= 33 dm²

Triangle rectangle.  (info +)

Tout triangle rectangle est la moitié d’un rectangle.

Comme vous l’avez vu en 6^ème   , vous pouvez dire que l’aire du triangle rectangle « ACB » est égale à

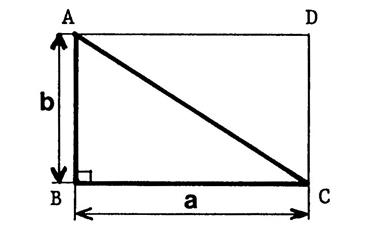
Triangle rectangle isocèle. ( info +)

« EFD » est un triangle isocèle rectangle en « D ».

Sachant que son aire est de 32 m²  .

Calculez les longueurs  « DE » et « DF ».

Corrigé :

1°)  Aire du carré 32 fois 2 = 64   ;

Solution1 : on sait que  8 fois 8 = 64 , DE et DF = 8 m

Solution 2 : on fait la racine carrée de 64 .

Fiche VII : exercices sur le triangle.

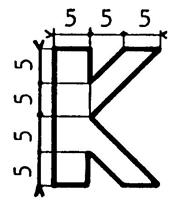
Activité 1 :

Calculez l’aire de la lettre « K » ci-contre. ( unité le m ).

Réponse : « par soustraction »

Calculez l’aire totale : 20 fois 15 = 300 m²  moins (5 fois 5 )= 25 et ( 20 fois 10 ) / 2= 100

 L’aire  de la lettre est 300 – ( 25 + 100) = 175 m²

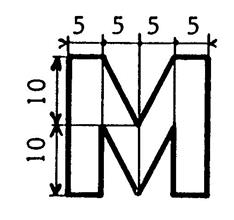
Activité 2 :

Calculez l’aire de la lettre « M » ci-contre. ( unité le m ).

Faire comme ci-dessus….

Calcul du plus grand rectangle et soustraire la valeur des 3 triangles….

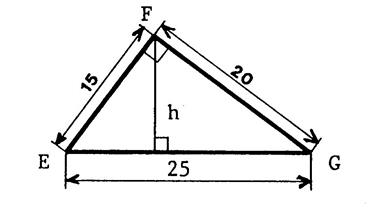
Activité 3 :

Ci-contre un triangle rectangle  « FGE » , les dimensions sont en cm.

Calculez la longueur de la hauteur « h » .

Corrigé :

( 15 fois 20 ) / 2 = ( 25  h ) /2 ;

 150  = 12,5 h    ;   h = 150 / 12,5 ; h =  12 cm

Vérification : faire le dessin et effectuez la mesure..

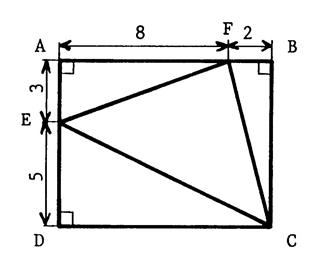
Activité 4 :

Voir la figure ci-contre :

Calculez l’aire du triangle « EFC ». ( l’unité est le cm.)

Corrigé :

Calculez l’aire du rectangle « ABCD » = 10 fois 8 = 80 cm²

Calculez l’aire du triangle :

AFE = 12 cm²

FBC =  8 cm²

ECD =  25 cm²

Faire la somme des aires …=  45 cm²

Soustraire la somme à l’aire du rectangle « ABCD » : 80 – 45 = 35 cm²

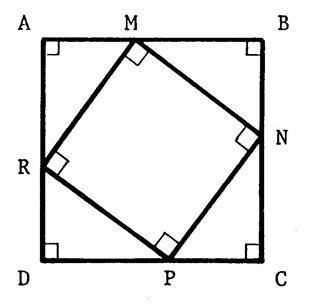
Activité 5 :

Voir la figure ci-contre :

« ABCD »  est un carré dont la longueur du côté est 14 m.

On a tracé à l’intérieur un carré « MNPR » tel que « AM = BN= CP = DR = 6 m » et par conséquent « MB= NC = PD = RA = 8 m »

Après avoir calculé l’aire du carré « MNPR », calculez la longueur de son côté.

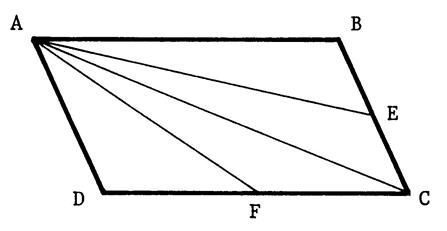
Activité 5 :

Voir la figure ci-contre :

« ABCD »  est un parallélogramme.

« E »  est le milieu de [BC]  et « F » le milieu de [ DC ].

Prouvez par un raisonnement que les triangles « ABE » , « AEC » , « ACF » , « AFD » ont la même aire.

Fiche VIII :  Aire du disque.  ( info ++)  et complément :longueur du cercle (circonférence)

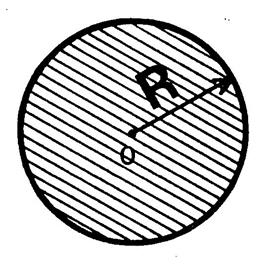
Ci-contre, la figure représente un disque de centre « O » et de rayon « R ».

Son aire est donnée par la formule ci-dessous.

( attention , n’oubliez pas que « R² »  remplace l’écriture du produit «  R  R »

A retenir : Aire du disque de rayon « R » :

     que l’on écrit aussi :    ou   

Attention : Ne pas confondre l’aire du disque et la longueur du cercle correspondant.

La longueur ( C )  d’un cercle de rayon « R »  est   :     ; autre écriture équivalente :  

Activité 1 :

a)       Un cercle a pour diamètre 20 cm. Quelle est la longueur de ce cercle ?  ( Prendre pour pi :   )

Réponse : R = 20 / 2 = 10  cm   ;  C = 2 fois 3,14  fois 10  = 62,8 cm

b)      Quelle est l’aire du disque correspondant ?

Réponse : R = 20 / 2 = 10  cm   ;  C 3,14  fois 10 fois 10   = 314 cm²

Activité 2 :

L’aire d’un disque est de 113,04 m²  . Calculez la longueur du rayon de ce cercle . ( on prendra )

Réponse :  3,14  fois R²  = 113,04 ;   R²  = 113,04 / 3,14   ; R² =  36   ;   R =    ; R = 6 m

Remarque : 

On peut parfois , pour faciliter les calculs prend pour pi la valeur de 22/7.

Faites la division de 22 par 7 :   (prendre 4 chiffres après la virgule : 3,1428571428571428571428571428571 )

Sachant que :  = 3,1415926535897932384626433832795

On peut dire que  22 / 7 est une bonne approximation de

Exemple : Aire du disque de rayon de 21 cm.

En cm² ;  A =   , or  21 = 3  7   donc   A =   =  1386 cm²

Activité 3 :

Chaque colonne du tableau ci-dessous correspond à un disque. Complétez ce tableau.

Rayon

7 cm

Longueur du cercle

43,96 cm

62,8 m

Aire du disque.

153,86 cm²

78,5 dm²

Activité 4 :

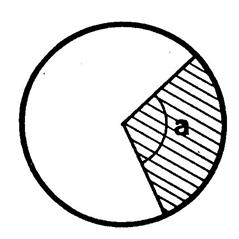
ci-contre vous est donné un secteur circulaire ( surface hachurée)

L’aire de ce secteur circulaire est proportionnelle à l’angle «  ».

Exemple .*Sachant que le cercle complet fait 360°.

-         Dans le cas où «  ». = 90°  , «  ». est le quart de 360°.

-         Donc l’aire du secteur circulaire correspondant sera le quart de l’aire du disque .

On vous demande de compléter le tableau ci-dessous correspondant à un disque de rayon égal à 30 cm. ( S = 3,14 fois 900 cm² = 2826 cm²)

Angle en degré

360°

180°

90°

60°

45°

55°

10°

Mesure de l’aire du secteur en cm²

2826 cm²

1413 cm²

706,5 cm²

471 cm²

353,25 cm²

431,75 cm²

78,5 cm²

Activité 5:

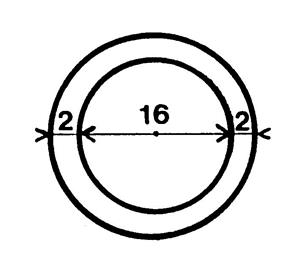
Autour d’un bassin circulaire de 16 m de diamètre on aménage une allée de 2 m de large .

Quelle est en m² l’aire de cette allée ?

Réponse :

Aire du grand disque : a)  R = (16 / 2 ) + 2 = 10 m ; b)  3,14 fois 10² = 314 m²

Aire du petit disque : a ) r = 8  m  ; b) 3,14 fois 8² = 3,14 fois 64 = 200,96 m²

Aire de l’allée : =  l’aire du grand disque moins l’aire du petit disque .

Soit : 314 – 200,96 = 113 , 04 m²

Fiche IX : Situations problèmes sur le calcul d’aire.

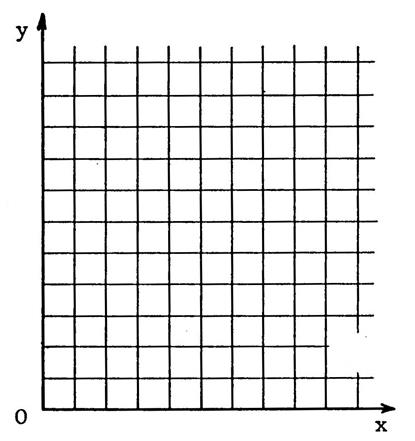
Situation 1 :

[ Ox     et    [Oy  sont des axes de coordonnées.

Placez les points dont on donne les coordonnées :

A ( 2 ; 8 ) ; B ( 5 ; 10 ) ; C ( 10 ; 7 ) ; D ( 8 ; 2 ) ; E ( 5 ; 1 ) ; F ( 2 ; 5 ).

Tracez le polygone « ABCDEF » .

Ce dessin est la représentation d’un champ à l’échelle :

Calculez l’aire (en are) de ce champ ( les carreaux ont 5 mm de côté) .

(vous pouvez faire des tracés sur le dessin pour compter les carreaux).

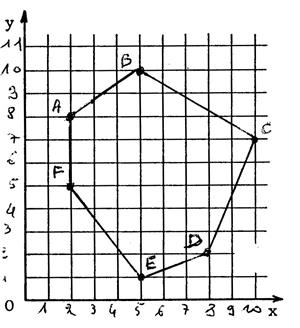
Corrigé : on place les points , on dessinne la figure .le polygone «  ABCDEF »

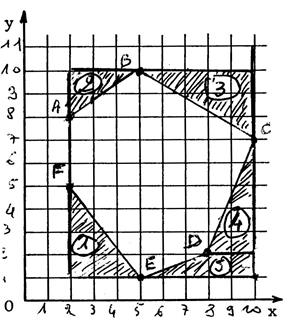
On s’aperçoit que le polygone est inscrit dans un rectangel de  8 carreaux sur 9

On décide de soustraire au rectangle les 5 figures identifiées .ci-dessous

Calculs des aires :

Aire du grand rectangle : 8 fois 9 = 72 carreaux.

Aire du triangle N° 1…. = 4 fois 3 divisé par 2 = 6

Aire du triangle N° 2…. = 3 fois 2 divisé par 2  = 3

Aire du triangle N° 3…. = 5 fois 3 divisé par 2 = 7,5

Aire du triangle N° 4…. = 5 fois 2 divisé par 2 =  5

Aire du trapèze  N° 5…. = (5 + 2 ) fois 1 divisé par 2  = 3,5

Aire des 5 surfaces numérotées : 6 + 3 + 7,5 + 5 + 3,5 = 23 carreaux.

Aire du polygone : 72 – 23 = 49 carreaux. Soit 49 fois 5 mm fois 5mm = 49 fois 25 mm² = 1225 mm²

Echelle =   soit     ; on fait le produit en croix : Surface réelle = 1225 fois 2 000 = 1 450 000 mm²   , soit 1,45 m²

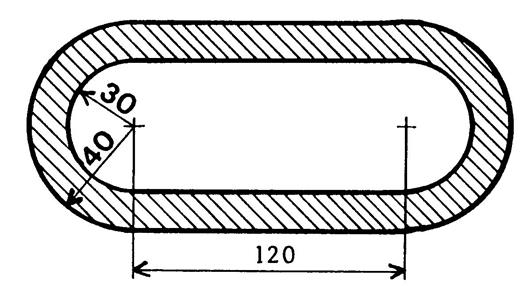
Situation 2:

Une piste de course à pied à la forme ci-contre ( partie hachurée ).
Les dimensions sont en « m ». Calculez son aire.

Surface limitée par le pourtour extérieur :

S = pi R²  + 120 fois 80  =  3,14 fois 40 ² + 9600 = 5024 + 9600 = 14 624  m²

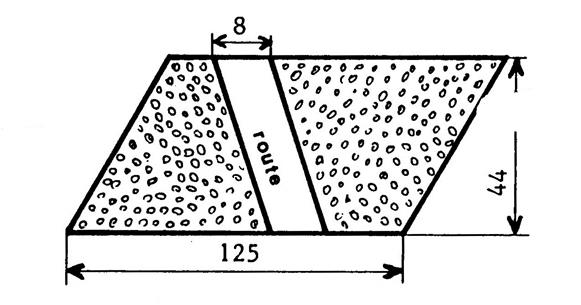
Situation 3:

Un champ à la forme d’un parallélogramme dont les dimensions ( en m) sont indiqués sur la figure ci-contre.

On construit une piste cyclable qui traverse ce champ.

Quelle est l’aire de la surface cultivable ?

Corrigé :

Aire du grand parallélogramme : 125 fois 44 =  5 500

Aire du petit parallélogramme :  8 fois 44 = 352

Aire de la surface cultivable :5 500 – 352  = 5148

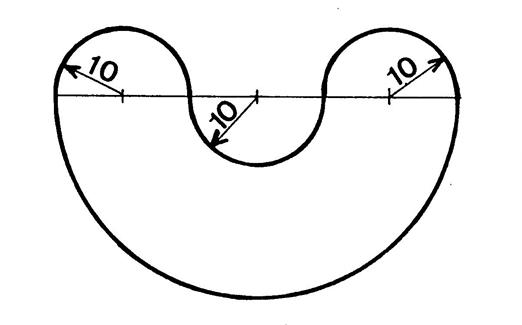
Situation 4:

Calculez le périmètre « P »  et l’aire « A »  de la surface ci-contre.

Les dimensions sont en dm.

Périmètre :

P = 3 fois le demi-cercle de rayon 10 + un demi-cercle de 30 dm de rayon

P = 3 fois 3,14 fois 10 + (3,14 fois 2 fois  30) divisé par 2 =94,2 + 94,2 = 188,4 dm

Aire :

Elle est constituées de 3 surfaces.

a)        3,14 fois 10²  = l’aire des deux demi-cercles de rayon 10 … = 314 dm² 

b)      ( 3,14 fois 30 ²  - 3,14 fois 10² ) divisé par 2 . ;   ( 2826 – 314 ) / 2  = 1256 dm²

c)      L’aire de la surface =  1256 + 314  = 1570 dm²

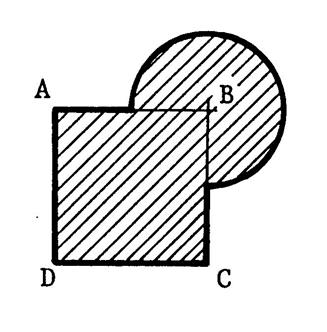
Situation 5 :

L’aire hachurée ci-contre a été dessiné en traçant un carré « ABCD » et un cercle de centre « B ».

Le diamètre du cercle et le côté  du carré ont la  même longueur : 24 cm.

a)       Calculez e périmètre « P » de cette surface.

b)      Calculez l’aire « A » de cette surface.

Périmètre :  Le périmètre est constitué par le ¾ du cercle de rayon 12 cm  et du ¾ du périmètre du carré de côté 24 cm .

 soit  (3,14 fois 12 fois 3) / 4 + 3 fois 24 cm = 28,24 + 72 = 100,26 cm.

Aire :

Et la somme de l’ aire du carrée + les ¾ de l’aire du disque .

Soit  24 ²  + 3,14 fois 12² fois 3 sur 4 =  576 + 339,12  = 915,12 cm²