|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
CORRIGE du DOSSIER : fiche collège 6ème : MESURE DES
AIRES
|
|
|
|
||||
|
|
1°) Surfaces équivalentes. |
|
||||
|
|
2°) Notion d’aire . |
|
||||
|
|
3°) Mesure d’une aire
. |
|
||||
|
|
4°) Changement d’unité
. |
|
||||
|
|
5°) Opérations- comparaison
. |
|
||||
|
|
6°) Encadrement de la mesure de l’aire d’une surface. |
|
||||
|
|
7°) Influence de l’unité sur la précision de l’encadrement. |
|
||||
|
|
8°) Unités d’aire, système métrique. |
|
||||
|
|
9°) Changement d’unité : conversion… |
|
||||
|
|
10°) Les mesures agraires . |
|
||||
|
|
11°) Aire du rectangle et
du carré et du triangle rectangle. |
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
Interdisciplinarité : |
|
|
|
|
TEST |
COURS |
1°) Interdisciplinarité: calculs… 2°) Arithmétique : les calculs
d’aires fiches pédagogiques.. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche de
travail |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
1°) Surfaces équivalentes. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
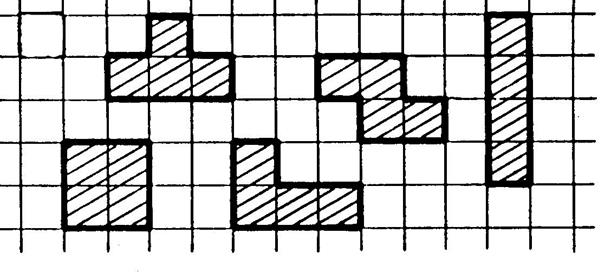
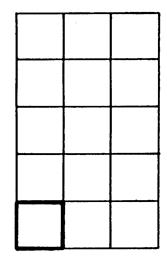
Activité 1 : Combien
de carreaux, comme ci-contre, faut-il pour recouvrir chacune des surfaces
hachurées ? ( 4 ) Remarque : On
constate que ces surfaces ne sont pas superposables, mais on peut les
recouvrir avec le même nombre de carreaux. On dira
d’elles que ce sont des surfaces
équivalentes. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
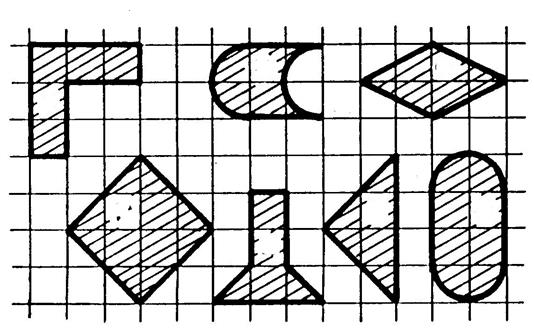
Le carreau ci-dessous
peut-être découpé en deux demi carrés ,
de surfaces équivalentes au carré ci-dessus :
Activité 2 :
Parmi les surfaces ci-contre, certaines sont équivalentes aux
précédentes ; nommez –les. ....…………………………..(
numérotez les surfaces..) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
2°) Notion d’aire . |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
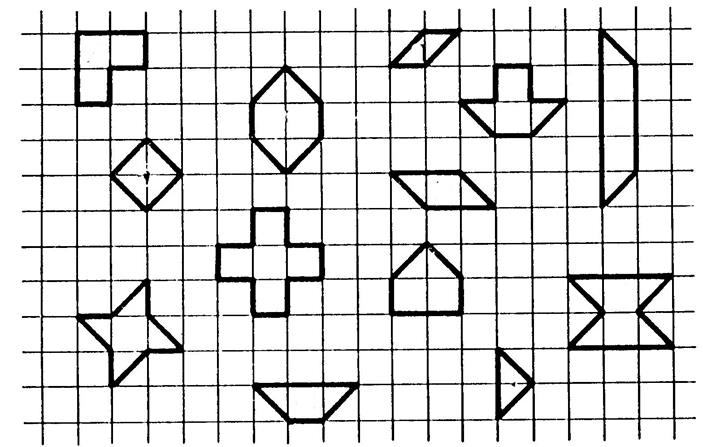
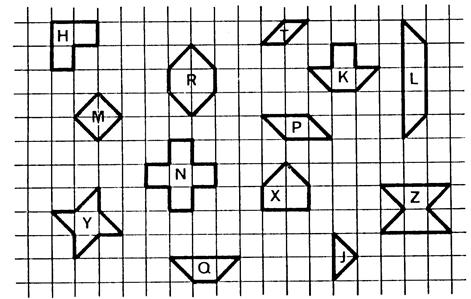
On vous a
représenté ci-contre 13 surfaces. ( numérotez les de
« 1 » à « 13 » en commençant en haut à gauche , ) Coloriez
avec une même couleur les surfaces regroupées
en surfaces équivalentes. Toutes
les surfaces qui appartiennent à un même groupe de couleur ont quelque chose
qui les caractérise : Elles ont la même
« étendue », on dit qu’elles ont la même aire. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
Toutes
les surfaces qui ont la même couleur
sont donc des surfaces équivalentes ; ce
qui signifie que les autres surfaces ne sont pas équivalentes, elles n’ont donc
pas la même aire. Aussi,
dire que des surfaces sont équivalentes revient à dire que leurs aires sont équivalentes. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
3°) Mesure d’une aire . |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
On a souvent
laissé penser que l’aire d’une surface ne s’obtenait que par calculs
(multiplication) .(oui , on fait des
calculs !) et pourtant avant d’apprendre à calculer , on a d’abord dû
apprendre à « mesurer » l’aire d’une surface , cette mesure s’effectuait en recouvrant une surface ( tel un carrelage) avec « des carrés » étalons , peut-être même un
ou des rectangles
« étalons » et ensuite
d’effectuer un comptage …(ici exemples ) L’aire du
carreau Dans le
premier chapitre , il fallait « 4 »
carreaux pour recouvrir chaque surface. On dit alors que la mesure de l’aire ( A ) de chacune de
ces surfaces est « 4 » . Avec
l’unité « u », « mesure de l’aire « A » égale
« 4 » » signifie
que l’ « aire de « A » = 4 u » . |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 3 : Avec la
même unité « u » , donnez l’aire des
surfaces désignées ci –contre. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Aire de H
= |
………………………. |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Aire de L
= |
…………………………… |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Aire de M
= |
……………………………….. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Aire de N
= |
………………………………. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
4°) Changement d’unité . |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
« p » , « r » , « g » sont des unités
d’aire. |
Unité « u » |
Unité « r » |
Unité « g » |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Lorsque
« u » est l’unité, quelle est la mesure de
« u » ?.........1... ; de
« r » ? …………2 ……..de
« g » ? ……………4………. Lorsque
« r » est l’unité, quelle est la mesure de
« u » ?........1/2.... ;
de « r » ? ………1……..de
« g » ? ……………2………. Lorsque
« g » est l’unité, quelle est la mesure de
« u » ?........ 1/4..... ;
de « r » ? ………1/2……..de
« g » ? ………1……………. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
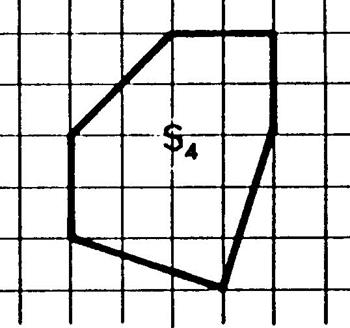
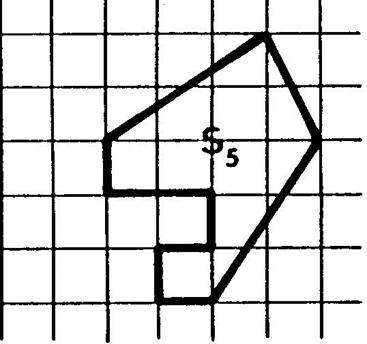
Activité 4 : On
vous demande de déterminer la mesure des aires des surfaces représentées
ci-dessous. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remplir
le tableau ci-dessous…… |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
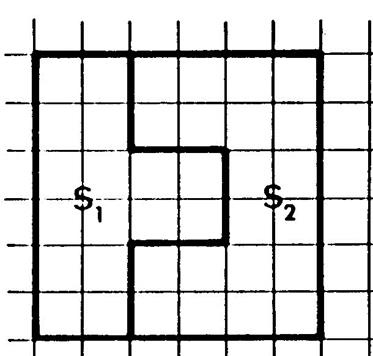
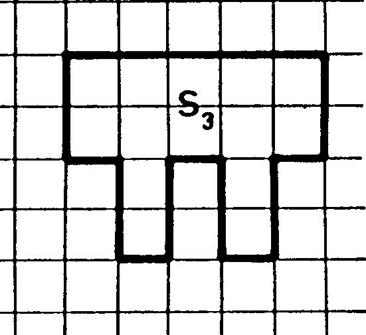
Remarque
la surface « S6 » est la réunion des surfaces « S1 »
et « S2 » |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
« S1 » |
« S2 » |
« S3 » |
« S4 » |
« S5 » |
« S6 » |
|
||||||||||||||||||||||||||||||||||||||||
|
Unité « p » |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Unité « r » |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Unité « g » |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous
constatez que la mesure de l’aire dépend de ……………l’unité………………………… choisie. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
5°) Opérations- comparaison . |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
·
Comme nous l’avons
dit « S6 » est la réunion de « S1 »
et « S2 » : Les
surfaces « S1 » et « S2 » ne se
« chevauchent » pas, elles n’ont en commun qu’une partie de la
frontière (dont la mesure de l’aire est égale à ……« S1 »
+ « S2 » ….) Vous
constatez que ,
quel que soit l’unité choisie, la mesure
de l’aire de « S6 » est la …………somme……………..des
mesures des aires de « S1 » et « S2 » . On écrit
alors (aire de « S6 ») = ( aire de S1 ») + ( aire de « S2 ») |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
·
Considérons les surfaces « S2 » et
« S5 » Vous
constatez que , quelle que soit l’unité choisie, la
mesure de l’aire de « S2 » est environ le ……double…….
de la mesure de l’aire de « S5 » |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
·
Considérons les surfaces « S3 » et
« S4 » (par
exemple) Vous
constatez que , quelle que soit l’unité choisie , la
mesure de l’aire de « S3 » est ……………. A la mesure de l’aire de « S4 » |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°5 En
utilisant les symboles : = (« égale ») ; (« supérieure à » ou « plus grande
que » ) > , (« inférieure à » ou « plus petite
que » ) < , classer
les surfaces ……. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
« S1 » |
« S2 » |
« S3 » |
« S4 » |
« S5 » |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
« S1 » |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
« S2 » |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
« S3 » |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
« S4 » |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
« S5 » |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
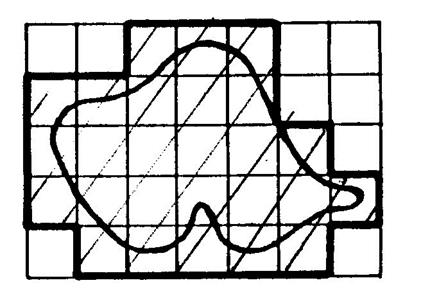
6°)
Encadrement de la mesure de l’aire d’une surface. |
( voir
« le carrelage » pour avoir une idée du découpage des surfaces en
carrés ) |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
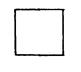
Soit l’unité de mesure de la surface le carré
ci -contre |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
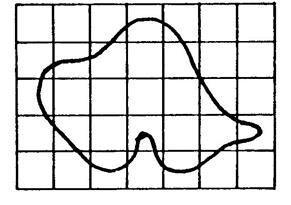
La figure
ci-contre représente une surface limitée par une courbe quelconque. Vous remarquez qu’il n’est pas possible de
recouvrir exactement cette surface par des carreaux « unités » |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
Mais on peut ,malgré
cela , tenter de proposer 2 solutions pour évaluer l’aire de la surface. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
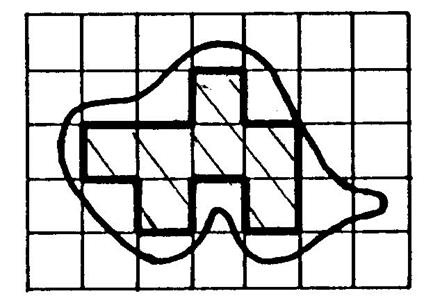
1ère :On peut recouvrir la surface partiellement par des
carreaux mais restant à
l’intérieur de la courbe. Voir ci-dessous. Combien
trouvez-vous de carreaux à l’intérieur ? ………….. |
2ème :On peut
recouvrir la surface totalement par des carreaux mais restant en débordant de la courbe. Voir ci-dessous. Combien
trouvez-vous de carreaux à l’intérieur ? ………….. |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
Nous
appelons « A » la mesure de l’aire
de cette surface (avec l’unité « u » ) . Ces deux
recouvrements, ci –dessus, nous permettent de donner un encadrement de
« A ». |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
………7………< A < ………26……… |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
7°)
Influence de l’unité sur la précision de l’encadrement. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
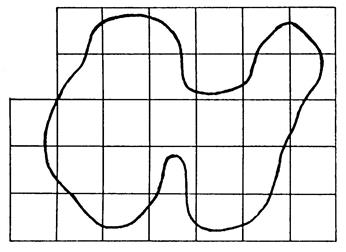
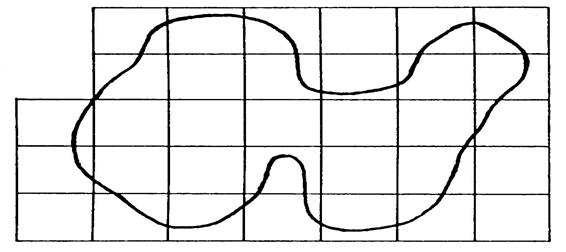
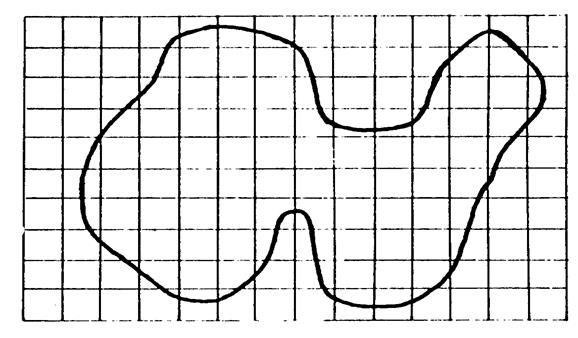
On vous a
représenté ci-dessous une courbe limitant une
surface « S ». |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
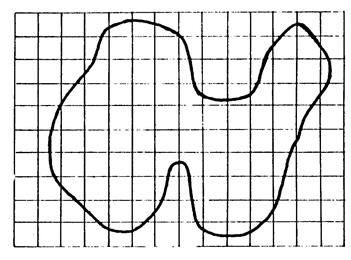
Figure 1 |
* |
Figure 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
Unité
« v » |
|
Unité « w » |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité N°6: |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Considérons
la surface « S » de la figure « 1 » avec l’unité « v » ·
Tracez le contour de
la réunion des carreaux situés à l’intérieur de la courbe.,
combien y a- t- il de carreaux ? ………7…… ·
Tracez le contour de
la réunion des carreaux nécessaires pour recouvrir totalement « S » . ., combien y a- t- il de
carreaux ? ………29…… Ces résultats vous permettent de donner un
encadrement de la mesure de « S ». Avec
l’unité « v » : 7 v
…………. < ( mesure de l’aire
de « S ») < …………29 v |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité N°7: |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Considérons
la surface « S » de la figure « 2» avec l’unité « w» ·
Tracez le contour de
la réunion des carreaux situés à l’intérieur de la courbe, combien y a- t- il
de carreaux ? …………… ·
Tracez le contour de
la réunion des carreaux nécessaires pour recouvrir totalement « S » , combien y a- t- il de carreaux ? …………… Ces résultats vous permettent de donner un
encadrement de la mesure de « S ». Avec
l’unité « w » : ………….
< ( mesure de l’aire de « S ») < ………… |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité N°8 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Sachant
que « v » = 4 « w » ,
à partir du dernier encadrement que vous venez de trouver, donnez un autre
encadrement de la mesure de l’aire « S » avec l’unité « v » . Avec
l’unité « v » : ………….
< ( mesure de l’aire de « S ») < ………… |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Si vous
comparez cet encadrement au premier que vous avez trouvé, que pouvez-vous en
dire ?.......................................................... |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
8°)
Unités d’aire, système métrique. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Important : Les unités d’aire sont définies à partir des unités de longueur, par
exemple : La figure
géométrique est un carré ( voir l’aire d’un carré) |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Le mètre carré est l’aire d’un carré dont la
longueur du côté est « 1 mètre » |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Il en est
de même pour les autres unités . ( que l’on appelle des sous multiples ou des multiples du mètre
carré) Ainsi , le décimètre carré est l’aire d’un carré dont la
longueur d’un côté est un décimètre… §
Le symbole du mètre
carré est « m² » . §
Le symbole du
décimètre carré est « dm² » §
Le symbole du
centimètre carré est …………….. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Considérons
un carré de 1 m de côté. Son aire
est donc : …1 m² …… ; Cherchons
combien il faut de petits carrés de « 1 dm » de côté pour recouvrir
exactement le grand carré. Puisque
« 1 m = …10..dm » on peut donc
placer sur une ligne une rangée de 10 petits carrés sur le
côté du grand carré. ( voir le dessin ci-contre) . Combien
de lignes (rangées) seront nécessaire pour couvrir la surface carrée
?............10................. Au total,
on a donc ……10……….rangées de ……10…..petits carrés. Le nombre
de petits carrés nécessaires pour recouvrir le grand carré est donc …10….. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
On peut écrire |
1 m²
= 100 dm² |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° 9 : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez
le tableau ci –dessous. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Unités |
Symbole |
Correspondance
avec le mètre carré. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
Sous - Multiples |
Millimètre carré |
mm² |
1 m² = |
1 00 00 00……………… mm² |
||||||||||||||||||||||||||||||||||||||||||||
|
Centimètre
carré |
cm² |
1 m² = |
1 00 00……………… cm² |
|||||||||||||||||||||||||||||||||||||||||||||
|
Décimètre carré |
dm² |
1 m² = |
1 00……………… dm² |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
Mètre
carré |
m² |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Multiples |
Décamètre
carré |
dam² |
1
dam² = |
0,01…………… m² |
||||||||||||||||||||||||||||||||||||||||||||
|
Hectomètre
carré |
hm² |
1
hm² = |
0,00 01………………
m² |
|||||||||||||||||||||||||||||||||||||||||||||
|
Kilomètre carré |
km² |
1
km² = |
0,00 00 01……………… m² |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque : Vous
constatez que les unités successives vont de « 100 » en
« 100 ». Donc dans
les changements d’unité, on découpera le nombre en « tranches »
de « 10 » chiffres. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Exemples : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
1°)
Convertir un mètre carré en décimètres carrés : -
1 m²
= ……100…..dm² ; -
Le décimètre carré est
donc la centième partie du mètre carré. -
1 dm² = |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
2°)
Convertir un mètre carré en centimètres carrés : -
1 m²
= ……1
00 00…..cm² ; ( soit 100 fois 100 ) -
Le centimètre carré
est donc la dix millième partie du
mètre carré. -
1 cm² = |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
3°)
Convertir un mètre carré en millimètres carrés : -
1 m²
= ……1
00 00 00…..mm² ; ( soit 1000 fois 1000 = 1 000 000 ) -
Le millimètre carré
est donc la millionième partie du
mètre carré. -
1 cm² = |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° 10 : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez : |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
1 dm² =
………………………………..mm² |
|
1 km² = …………………………..mm² |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
1 cm² = …………………………..dam² |
|
1 hm² = …………………………..cm² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
( PS : si
vous avez des difficultés , il faut
utiliser le tableau de conversion ci- dessous …) |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
9°)
Changement d’unité : conversion… |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Pour effectuer
des changements d’unités, il est parfois intéressant de savoir refaire le
tableau de conversion ci-dessous. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0, |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
0, |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
0, |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Attention : ici les explications pour utiliser et exploiter ce
tableau !!!! |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
5 |
8 |
7 |
0 |
3 |
9 |
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Nous avons
placé un nombre dans le tableau ci-dessus ! |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(valeur relevée dans le tableau) |
( soit le nombre à lire ) |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
On peut
lire indifféremment : |
5 87 03,94
m² |
58 703,94
m² |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Ou |
0, 05 87 03 94
km² |
0, 05870394
km² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Ou |
5, 87 03 94
hm² |
5, 870394
hm² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Ou |
5 87 , 03 94 dam² |
587 ,
0394 dam² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Ou |
5 87 03
94 dm² |
5 870 394
dm² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Ou |
5 87 03 94 00
cm² |
587 039 400
cm² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Ou |
5 87 03 94 00 00
mm² |
58 703 940
000 mm² |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 11 : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
En
faisant les conversions En plaçant dans le tableau les nombres donnés ,
faites les conversions suivantes : |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
13 km² 54 hm² 17 dam² 69 m² = |
23541778….m² |
…2354,1778….hm² |
|
||||||||||||||||||||||||||||||||||||||||||||
|
43 m² 17
dm² 5 cm² = |
431705….cm² |
43170500….mm² |
||||||||||||||||||||||||||||||||||||||||||||||
|
5 dam² 8
m² 68 dm² |
50868….d
m² |
… 0,00 05 08 68…….km² |
||||||||||||||||||||||||||||||||||||||||||||||
Corrigé :
|
|
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
|
|
|
|||||||
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ |
|
|
5 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ |
|
|
|
|
1 |
7 |
|
|
|
|
|
|
|
|
|
|
|
||
|
+ |
|
|
|
|
|
|
7 |
8 |
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
3 |
5 |
4 |
1 |
7 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
1 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
1 |
7 |
0 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
6 |
8 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
5 |
0 |
8 |
6 |
8 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Activité 12 : |
|
||||
|
|
En faisant
les conversions mentalement , complétez le tableau
ci-dessous dans lequel chaque colonne correspond à une même aire exprimée
avec des unités différentes . |
|
||||
|
|
|
Colonne dam² |
Colonne m² |
Colonne mm² |
Colonne cm² |
|
|
|
mm² |
1
580 000 000 |
9000 |
7800 |
425 |
|
|
dam² |
15,8 |
0,00009 |
0,00 00 78 |
0,00000425 |
||
|
m² |
1580 |
0,009 |
0,0078 |
0,000 425 |
||
|
cm² |
15 800 000 |
90 |
78 |
4,25 |
||
|
|
|
|
||||
Aide au corrigé :
|
|
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
7 |
8 |
0 |
0 |
|
|
|
||
|
|
|
|
|
|
1 |
5 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
|
|
|
||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
4 |
2 |
5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10°)
Les mesures agraires : |
|
|
|
|
|
|
|
|
|
Pour exprimer
les mesures des aires des terrains , champs , bois ,
en immobilier , on utilise des unités particulières…… |
|
|
|
|
(voir le
tableau ci-dessous) |
|
|
|
|
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
hectare |
|
are |
|
centiare |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ha |
|
a |
|
ca |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Les 3
unités couramment utilisées sont : l’are ,
l’hectare et le centiare. |
|
|
|
|
·
L’are ; symbole « a » qui vaut
« 1 dam² ». |
1 a
= ……100……
dam² |
|
|
·
L’hectare ;
symbole « ha » qui
vaut « 100 ares » . |
1 ha = …100………a… |
||
|
·
Le centiare ;
symbole « ca » qui vaut
1 centième d’are ( = 1 m² ) |
1 a
= ….. 100 …….. ca |
||
|
|
|
|
|
|
|
Quelle
est l’unité du système métrique qui correspond au centiare ? 1 ca = ……1…….m² , 1 a = …100….m² ;
1 ha = …10 000….m² |
|
|
|
|
|
|
|
|
|
Activité n°13. : |
|
|
|
|
L’aire
d’un terrain est de 85 300 m² , on vous demande
d’ exprimer cette aire en hectare , en are
et en kilomètre carré. |
|
|
|
|
|
|
|
|
|
Réponse :
85 300 m² = 8, 5 ha = 850 a
= 0,085 km² |
|
|
Corrigé
|
|
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
hectare |
|
are |
|
centiare |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ha |
|
a |
|
ca |
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
0 |
8 |
5 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
1 |
3 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
2 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
6 |
8 |
3 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
9 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Activité n°14 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Un terrain
de 9 hectares est divisé en parcelle de 1 800 m² chacune. Quelle
est le nombre de parcelles ? |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Réponse :
on convertit : 9 ha = 90 000 m² ; nombre de parcelles : 90 000 / 1800 = 50 parcelles . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°15 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On vous
demande de ranger dans l’ordre croissant les aires suivantes ( en utilisant le symbole « < » )
: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
72,7 m² |
|
0, 8138 a |
|
0,000 145 km² |
|
72,55 ca |
|
0,00 6836 ha |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voir ci-dessus le tableau. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
68,37 m² |
< |
72,55 m² |
< |
72,7 |
< |
81,38 |
< |
145 m² |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0,006836 ha |
< |
72,55 ca |
< |
72,7 m² |
< |
0,8138 a |
< |
0,000 145 km² |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
11°)
Aire du rectangle et du carré et du
triangle rectangle. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A ) Aire du rectangle |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ci -contre
on vous a représenté un rectangle dont les dimensions
sont : « 5 cm » et « 3 cm ». On vous
demande de chercher combien il faut de carrés de 1 cm de côté pour le
recouvrir entièrement. Sur la largeur ,on peut placer une rangée de ……3…carrés Combien de
rangées seront nécessaires pour « remplir » la surface ? …5…. Donc le
nombre de carrés nécessaires pour le recouvrement est donc le produit de : 3 ·
L’aire du petit
carré étant de 1 cm². ·
L’aire du rectangle
est donc de 15
cm² |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Constat : on vient de voir que
pour obtenir l’aire d’un rectangle,on
a multiplié la mesure de sa longueur par la mesure de sa largeur. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
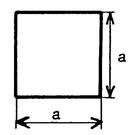
|
« a »
et « b » étant les dimensions d’un rectangle, (
exprimées avec la même unité) l’aire « A » de ce rectangle
(avec l’unité correspondante à la puissance « 2 ») est « A =
a |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Le
raisonnement ci-dessus a été fait avec des nombres entiers. Dans le cas
de nombres à virgules ( dit aussi :
nombres décimaux), il suffit d’imaginer un changement d’unité
donnant des nombres entiers et on se retrouve dans la situation précédente.. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°16 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez
l’aire d’un rectangle dont les dimensions sont : « 2,5 m » et
« 76 cm » |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Corrigé : convertir
2,5 m = 250 cm ; Aire :
250 cm |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°17 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
L’aire d’un
champ rectangulaire est de 93 ares. La mesure
de l’un des côtés est de 124 m. Quelle est la mesure de l’autre côté ? |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Corrigé :
93 ares = 9300 m² ;
9300 / 124 = 75 m |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Le carré
est un rectangle particulier dans lequel
« a = b » Ce qui
revient à dire que la mesure de la longueur est égale
à la mesure de la largeur. L’aire du
carré est alors « A = a |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Rappel :
le périmètre « P » du carré est égal
« 4 » fois la longueur de « a » soit la formule : P
= 4a |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
·
Convention d’écriture : |
Info
plus sur les conventions d’écriture sur les puissances … |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« a » étant un nombre quelconque, « a |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Lecture de l’écriture : « a² » : On dira
indifféremment : « « a » au carré » ; « a »
exposant « 2 » ; « a »
puissance « 2 »
. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Info : Pour éviter
la confusion entre la lettre « x »
et le signe de l’opération « |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ainsi : On sait
que « 3 On sait
que « 5 On dit
que « 9 » est « le carré de « 3 » » . De même « 25 » est « le carré de « 5 » ». |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A retenir : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Si on désigne « a »
comme étant le nom donné au
côté d’un carré ( avec une unité déterminée : …,cm, dm, m , …….) l’aire « A » de ce carré ( avec l’unité
correspondante : …,cm², dm²,
m² , …….) est « A = a² ». |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Par
exemples : ·
si l’unité de la
mesure de longueur déterminée est le
« m » , l’unité d’aire obtenue sera des « m² » . ·
si l’unité de la
mesure de longueur déterminée est le
« cm » , l’unité d’aire obtenue sera des « cm² »
. ·
si l’unité de la
mesure de longueur déterminée est le
« dm » , l’unité d’aire obtenue sera des «dm² »
. ·
……………………………. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°18 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
La longueur
du côté d’un carré est de « 12 cm ». Quel est
le périmètre de ce carré ? ………………………………….. Quelle
est l’aire de ce carré ? ………………………………………….. (attention à l’unité !! ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°19 : Calcul numérique (info
++ : les carrés des nombres entiers ) . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez
le tableau donnant les « carrés »
des « 11 » premiers
nombres entiers naturels. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a² |
0 |
1²=1 |
2²=2 |
3²=3 |
4²=4 |
5²=5 |
6²=6 |
7²=7 |
8²=8 |
9²=9 |
10²=10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n°19 : |
( pré
requis : savoir
obtenir la valeur de la racine carrée
d’un nombre » |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a) Quelle est la longueur d’un carré dont l’aire est « 0,0064
m² » ? b) Quelle est la longueur d’un carré dont l’aire est « 625
cm² » ? |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° 20 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
L’aire
d’un carré est « 40 m² » .On appelle « a » la mesure en
« m » de son côté. Calculez
les valeurs approchées à « 0,1 prés par défaut
et par excès de « a ». |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C ) Aire du triangle rectangle. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
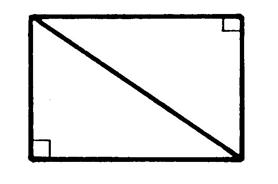
Prenez
une feuille. (voir ci-contre) Dessinez
un rectangle et découpe –le. Coupez-
le en deux suivant une diagonale. Vous obtenez deux triangles
rectangles. Faites
les superposés. Sont-ils superposables ? …….oui… Ils ont
donc la même « aire » …. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
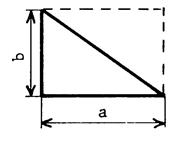
En
appelant « a » et « b » les mesures des côtés
perpendiculaires, vous pouvez dire que l’aire du triangle rectangle est A = ( a Soit l’aire du triangle
rectangle est égale à l’aire du
rectangle divisée par « 2 ». |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité n° 21 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez
l’aire d’un triangle rectangle dont les côtés perpendiculaires ont pour
longueur « 12 cm » et « 15 cm ». |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
12°)
Activités :
Situations problèmes |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Longueur |
44 mm |
…1,5 dm .dm |
1,3 cm = 13 mm |
5,2 dm |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Largeur |
2,5 cm |
8 cm = 0,8 dm |
…169 / 13 =…13.mm |
1,74 / 2 = 0,87 = 8,7 dm ………………..m |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Périmètre |
(44 + 25)2 = 138 …………………mm |
…46…..cm |
1,3 fois 4 =…5,2…cm |
1,74 m |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Aire |
4,4
fois 2,5 = 11 ……………….cm² |
1,2 dm² |
169 mm² |
……45,24..dm² |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
B) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Un
terrain rectangulaire a pour dimensions « 55 m » et « 46 m ». On y
construit une maison rectangulaire de « 10 m » sur « 16
m » Calculez
l’aire du terrain restant. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Aire du terrain : 55 fois 46 = 2530 m² ; aire de la maison : 160 m² ;
aire du terrain restant : 2530 –
160 = 2370 m² |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
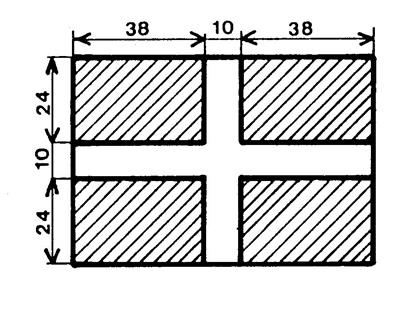
Le
dessin ci-contre représente un
drapeau. Les
dimensions sont en « cm » ; Calculez
l’aire de la croix blanche. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
86 fois 10 = 860 cm² +
2 fois ( 24 fois 10) = 860 cm² + 480 cm² =
1340 cm² |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
D ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
L’aire de
la surface de la France est environ « 550 000 km² » , la population
française est d’environ 60 500 000 habitants. 1°) En
imaginant que l’on répartisse équitablement le sol français entre chaque
habitant, quelle surface chaque français aurait-il ? 2°) Si
cette parcelle était carré, quel en serait la longueur du côté ? |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1°) 550 000 / 60 500 000 = 0,009 km². (environ) = 9 000 m² ou 9090 m² 2°)
environ 95 m de côté. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
E ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
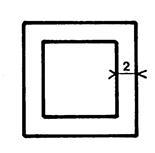
Le dessin
ci-contre représente un bassin carré entouré par une allée de « 2
m » de large. L’aire de
l’allée est de « 80 m² », calculez le côté du bassin. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 ( X + 4 ) + 2x = 80 ; 2x + 8 + 2x = 80 ; 4 x + 8 = 80 ; 4x = 80 – 8 ; 4 x = 72 ; x = 72 / 4 ; x = 18 m |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
En plus
Lecture MESURE d’AIRE
La bordure d’un terrain délimite une étendue
qu’on appelle « surface » , ou
« superficie » , ou « aire » du terrain. Comme on a inventé une unité ( le
mètre ) et ses multiples ou sous multiples
pour mesurer les longueurs (
l’outil le lus courant étant une règle de 1 mètre )
, On a inventé
une unités de base « le carré d’un mètre
de côte » dit couramment : « mètre carré » pour « apprécier » l’étendue des
surfaces : ce sont des
« carrés » qui ont pour côté les unités de longueur pré définies
ci-dessus . L’unité principale est le « mètre carré » , qu’on écrit « m2 » .On
trouvera des sous multiples et des multiples du m². ( voir
le carrelage pour avoir une idée du découpage des surfaces en carrés ) Vocabulaire : « Mesure
d’ une aire ou surface » On appelle « mesure » de surface ou de «mesure d’une superficie »
les mesures dont ont
se sert pour évaluer l’étendue considérée sous les deux dimensions longueur
et largeur . Remarques : a) si l’on acheter un fil d’antenne de télévision seule la longueur de ce fil
nous intéresse . On le considère comme une ligne qui
n’a qu’une seule dimension : sa longueur . b)
Si l’on veut acheter un tapis
pour la salle de séjour , on le choisit d’une
surface convenable . Il faut tenir compte des 2 dimensions du tapis :
longueur et largeur . Mesurer une surface
IV) LES
UNITES DE MESURES D’AIRE
On utilise deux types d’unités de mesure : A ) les unités de mesures de
superficie proprement dites ; B ) les unités de mesures agraires. Se souvenir que l’on ne mesure pas l’aire d’ une surface
(trop long à faire) on la
calcule . Remarque :pour mesurer une surface , il est
nécessaire de choisir une unité . A) les
unités de mesures de superficie proprement
dites 1°) Unité –
l’unité des mesures de surface est le mètre carré. Le mètre carré ( m2 ) est la
superficie contenue dans un carré de 1 mètre de côté . Les unités de surface sont :
2°)Numération
- Les unités de surface
suivent la loi « centésimale » , c’est à dire qu’elles sont de cent
en cent fois plus grandes ou plus petites. Ainsi il
faut 100 m2 pour faire 100
dam2 ; 100 dam2 pour faire 1 hm2 ; et 1 dm²
= 100 cm² B) les
unités de mesures agraires. 1°)Définition : on appelle « mesures agraires » les mesurent qui
servent à évaluer la superficie des propriétés foncières , comme celle des
champs , des bois , etc.,… 2°) Unité :
l’unité des mesures agraires est l’ « are » .
L’are ( « a »)
est une surface qui égale un
décamètre carré . ( = 100 m²) Multiple
et sous multiple : L’are n’a qu’un multiple ,
l’hectare , et un sous multiple le centiare. L’hectare ( ha) égale
100 ares ( = 10 000 m²) ; Le centiare ( ca) égale
la 100e partie de l’are ( = 1 m²). C )
Choix de l’unité .
Dans les travaux
de menuiserie , de maçonnerie , de peinture ,
etc. , on prend pour unité de surface le mètre carré . Pour évaluer les surfaces de petite étendue ( feuille de verre , de papier , etc. , on prend
généralement pour unité le centimètre carré . Quand on évalue les grandes superficies
, comme l’étendue d’un département , d’un Etat , on prend pour unité
le kilomètre carré , et quelques fois
l’hectomètre carré ; ces mesures sont alors appelées
« mesures topographiques » TRAVAUX AUTO FORMATIFS. CONTROLE : 1°)
Qu’appelle-t-on
« surface » ; « superficie » , « aire » ? (voir le
dictionnaire) 2°)
Qu’a-t-on inventé pour apprécier
une surface ? 3°) Quelle est l’unité principale ? 4°) Que signifie « mesure d’une
surface » 5°) Citer les différentes mesurent de surface 6°) Compléter la phrase : Se souvenir que
l’on ne mesure pas l’aire d’ une surface (trop long à faire) ………………….. 7°) Si l’on veut mesure
une surface que faut-il choisir : :…………………………… 8° l ‘ unité
de mesures de superficie proprement
dites : a) Quelle est son unité ? b) Quel est
son symbole ? ……….. c) Que représente un mètre
carré ?…………………………………………………………………………… d) Compléter le tableau : Les unités de surface sont :
Compléter les phrases
suivantes Numération - Les unités de surface suivent la loi ………………… ,
c’est à dire qu’elles sont ………………………………… Ainsi il
faut 100 m2 pour faire ………….. ; 100 dam2 pour
faire …………… e) Choix
de l’unité .
Dans les travaux
de menuiserie , de maçonnerie , de peinture ,
etc. , on prend pour unité de surface ……………….. . Pour évaluer les surfaces de petite étendue ( feuille de verre , de papier , etc. , on prend
généralement pour unité ……………………. . Quand on évalue les grandes superficies
, comme l’étendue d’un département , d’un Etat , on prend pour unité ………………… , et quelques fois ………………… ;
ces mesures sont alors appelées « ………………………… »
9°) les
mesures agraires. a) Donner la définition :
: ……………………………………………………. b) Quelle est l’unité ? : ……………………………….. c) Symbole ? : …………. d) A quoi est égale l’are ? …………………………………………………. e) Citer son multiple et sous multiple : …………………………………………………………………….. d) compléter : L’hectare ( ha) égale ………. ares ; Le centiare ( ca) égale
la …………………. de l’are . EVALUATION : Refaire toutes les activités contenu dans ce document……………. 1°) Dessiner un rectangle : un de 6cm de
long et de 2 de large et un autre de 4
cm de long et 3 cm de large . Quadrillez – les en carreaux de 1 cm de côté ( cm2
). Numéroter
les carreaux . Combien de carreaux y – a – t- il dans chaque rectangle ? Que peut-on dire de la surface de ces deux rectangles , bien qu’ils ne se ressemblent pas ?
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||