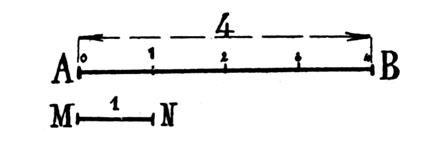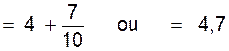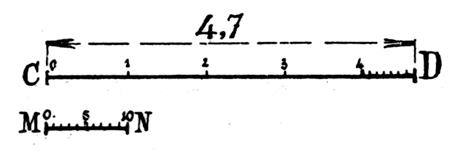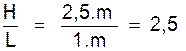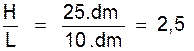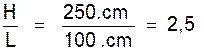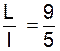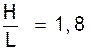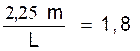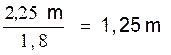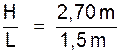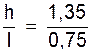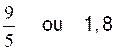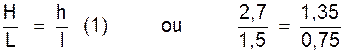Nous comptons des unités distinctes, nous mesurons des grandeurs continues : le résultat (dit : grandeur) s’exprime par un nombre suivi du nom de l’unité.

Info : le nombre associé à une unité est appelé : scalaire »

Les unités couramment utilisées sont celles rencontrées dans la vie quotidienne , elles sont en rapport avec les mesures de :

Longueurs ; masse ; capacités , et toutes celles que nous dénombrons ( assiettes ,verre ; cuillères ; chevaux , moutons , planches , élèves , tout ce qui peut de compter et appartenant à la même « classe » , groupe ou caractère.

Mesurer une grandeur : @ info « UNITE »

Mesurer une grandeur , c’est la comparer à une autre grandeur connue et de même espèce appelée « unité »

UNITE :

L’unité est chacun des objets que l’on compte , ou la mesure qui sert à évaluer une grandeur de la même espèce .

La mesure d’une grandeur :

La mesure d’une grandeur est le résultat de l’opération qui consiste à chercher combien de fois la grandeur à mesurer contient une autre grandeur de même espèce prise comme unité.

Nature du nombre exprimant le résultat de la mesure :

Le résultat de la mesure d’une grandeur peut donner : @ info

1°) Un nombre entier .

Exemple

AB contenant 4 fois MN , on a par suite : mesure de AB = 4

2°) Un nombre fractionnaire .

Exemple : CD contenant 4 fois MN + 7 fois le dixième de MN on a

La mesure de CD

3°) Un nombre « incommensurable » @ info

Exemple :

Si l’on mesure la diagonale « d » d’un carré en prenant comme unité de mesure le côté « a », on ne trouve aucune partie de l’unité « a » contenue un nombre exact de fois dans « d » , on dit qu’il n’y a pas de « commune » mesure entre « d » et « a » , le résultat de la mesure est un nombre incommensurable . Dans le cas de la figure ce nombre est

Dans la pratique des opérations , on se contente d’une mesure approchée de la grandeur donnée et l’approximation varie avec la nature de la mesure à effectuer.

RAPPORT DE DEUX GRANDEURS :

On appelle « rapport de deux grandeurs » le quotient exact de leurs mesures obtenues avec une même unité.

Exemple : les dimensions d’une porte obtenues a l’aide :

du mètre sont H = 2, 5 .m et L = 1 .m .

Le rapport de ces dimensions sont :

Mesurées ave c un décimètre sont H = 2 5 .dm et L = 10 .dm .

Le rapport de ces dimensions sont :

Mesurées ave c un centimètre sont H = 2 5 0 . cm et L = 100 .cm .

Le rapport de ces dimensions sont :

Quelle que soit l’unité employée pour la mesure , le quotient exact est toujours « 2,5 »

Par suite :

Le rapport de deux grandeurs est un nombre constant quelle que soit l’unité ayant servi à mesurer ces grandeurs.

Applications numériques .

Le rapport des dimensions d’une scène de théâtre est , trouver la longueur « L » si la largeur « l = 12,25 m » .

On a d’après la définition du rapport de 2 grandeurs :

d’où L = l ´ = 12,25 m ´= 22,95 m

2°) le rapport de la hauteur d’une fenêtre « H » à sa largeur « L » doit être de « 1,8 ».

Trouver la largeur si la hauteur est de 2,25 m .

On a d’après la définition du rapport de 2 grandeurs : ou , en remplaçant « H » par « 2,25 m » :

On en tire :

2,25 m = 1,8 ´ L et donc L =

PROPORTIONS : ( @ « notion »)

A) Une proportion est l’égalité entre deux rapports.

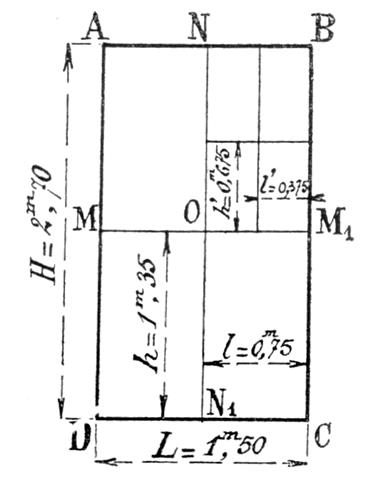
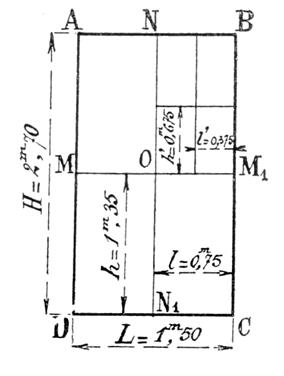
Le rectangle représenté ci contre donne

Les points « M » et « M ₁ »,« N » et « N ₁ » , étant les milieux des côtés du 1^er rectangle on a :

La valeur commune de ces deux rapports est

On a donc :

ces deux égalités sont des proportions .

B) La division en deux parties égales des côtés du rectangle ONBM , étant effectuée , on peut écrire :

(2)

ces deux séries d’égalités constituent des suites de rapports égaux .

La proportion (1) permet de dire que les grandeurs « H » et « h » sont proportionnelles aux grandeurs « L » et « l » , et la suite de rapports égaux (2) permet de dire que les grandeurs « H » , « h » et « h’ » sont des grandeurs proportionnelles aux autres grandeurs « L » , « l » et « l’ » .

APPLICATION : Figures semblables ( @info)

La géométrie appelle « figures semblables » celles qui ont leurs angles égaux et leurs lignes ou dimensions correspondantes proportionnelles.

Les différents rectangles de la figure de l’exercice précédent ,et repris ci contre sont donc des rectangles semblables .

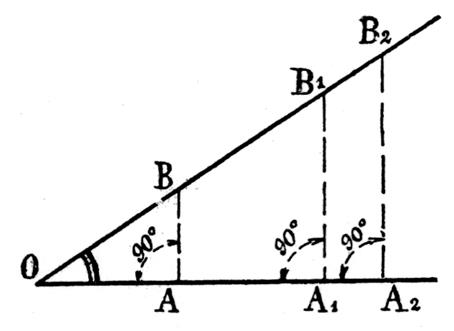
On démontre en géométrie que deux triangles ayant deux angles respectivement égaux sont semblables.

La figure ci contre obtenue en abaissant des points B , B₁ ,et B ₂ des perpendiculaires sur OA donne donc des triangles rectangles OAB , O A 1 B 1 et O A 2 B 2 semblables . ON en déduit que les côtés correspondants ou homologues de ces triangles proportionnels.

Cette propriété importante nous conduit à la définition des lignes trigonométriques d’un angle aigu.

Autres définitions : Nombres concrets et nombres abstraits :

« Nombre concret » : un nombre est concret lorsqu’on indique la nature de son unité ; ainsi : 29 élèves, 7 mètres, 5 litres, sont des nombres concrets ;

7 m et 5 litres sont aussi des grandeurs (parce que c’est avec une mesure « étalon » que l’on mesure)

« Nombre abstrait » si l’on ne fait qu’indiquer la quantité sans spécifier sa nature , on a un nombre abstrait ; huit ; vingt cinq , trente sont des nombres abstraits .

Travaux auto formatifs.

Travaux : CONTROLE:

Rechercher les définitions des mots suivants :

1. « GRANDEUR » :

2. « Evaluation d’une grandeur »

3. « Mesurer une grandeur »

Corrigé : CONTROLE:

Rechercher les définitions des mots suivants :

« GRANDEUR » :

on appelle « grandeur » ou « quantité » tout ce qui peut-être augmenté ou diminué .

Une grandeur est un nombre associé à une unité .

« Evaluation d’une grandeur »

Evaluer une grandeur , c’est se faire une idée exacte de son importance , de sa valeur .

« Mesurer une grandeur »

Mesurer une grandeur , c’est la comparer à une autre grandeur connue et de même espèce appelée « unité »

EVALUATION:

Donner des exemples :