DOCUMENT INTERACTIF.
|
Inventaire des principaux exercices types de CAP Industriel .(Niveau
V
bis) Pour
valider la formation ,Il faut savoir faire l’ensemble des exercices et problèmes. |
|
NOM : |
Prénom |
|
Date : |
|
|
Etablissement : |
Feuille :
SUITE :
niveau V |
|||
|
Devoir sommatif : |
Si vous avez accès au logiciel : Cliquez
sur le
point vert
pour obtenir
Corrigé |
Consignes :
Formation
complémentaire :
Les
32 exercices ou situations problèmes renvoient à un cours
spécifique.( 1
exercice = 1 cours )
Vous
devez vous
faire évaluer : ( 1
exercice = 1 devoir ) et
( 32 exercices = 32 semaines de formation)
► Les 32 exercices ou équivalents sont à passer , en
devoir , sur
l’année
scolaire ( soit
1 exercice par semaine ; ou 2 exercices tous les quinze
jours ; ……)
.► Le minimum à
passer :
10 exercices par
trimestre ( la moyenne
de la note est
calculée sur
8 notes ,
ce qui signifie que si vous n’avez passé que
5 devoirs vous
avez 3 notes égales à 00 / 20 comptabilisées
)
FICHE DE SUIVI :
|
Cours |
Date |
note |
validation |
|
|
Cours |
date |
Note |
validation |
|
1.
|
|
|
|
18 |
|
|
|
||
|
2.
|
|
|
|
19 |
|
|
|
||
|
3.
|
|
|
|
20 |
|
|
|
||
|
4.
|
|
|
|
21 |
|
|
|
||
|
5.
|
|
|
|
22 |
|
|
|
||
|
6.
|
|
|
|
23 |
|
|
|
||
|
7.
|
|
|
|
24 |
|
|
|
||
|
8.
|
|
|
|
25 |
|
|
|
||
|
9.
|
|
|
|
26 |
|
|
|
||
|
10. |
|
|
|
27 |
|
|
|
||
|
11. |
|
|
|
28 |
|
|
|
||
|
12. |
|
|
|
29 |
|
|
|
||
|
13. |
|
|
|
30 |
|
|
|
||
|
14. |
|
|
|
31 |
|
|
|
||
|
15. |
|
|
|
32 |
|
|
|
||
|
16. |
|
|
|
33 |
|
|
|
||
|
17. |
|
|
|
34 |
|
|
|
Méthodologie :
En début d’année , vous
aller sûrement
passer les devoirs que vous savez faire sans problème. Cela
vous laisse du temps pour compléter votre formation .Demander
alors le cours qui correspond à
l’exercice que vous ne savez pas faire .(prévoir
un délai de 8 jours entre la demande et le cours reçu). Chaque
cours « papier » est accompagné d’un
travail destiné à l’auto formation.
Ce travail est à rendre. A
la fin de chaque cours étudié
un devoir spécifique à
ce cours peut être exigé .
|
NOM : |
Prénom : |
|
Date : |
|
|
Etablissement :ou Classe : |
Feuille :
|
|||
|
1
°) Ranger les nombres suivants par ordre de grandeur croissante : |
SOS cours et |
15,006 ;
15,016 ; 15,061 ; 15,601 ; 15,106
|
|
|
|
|
|
2°) Exprimer en heures, minutes, secondes :
|
Durée. |
h |
min. |
s. |
|
4730
s |
|
|
|
|
1803
s |
|
|
|
|
85
450 s |
|
|
|
Réponse : 2 possibilités : la calculatrice ou manuellement ;« Manuellement » :
faire la division par « 60 »
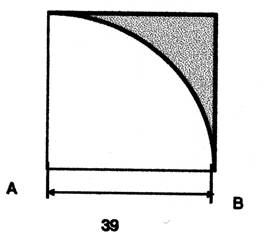
3°) Calculer
l’aire des surfaces ombrées :
|
Suite |
|
figure 1
|
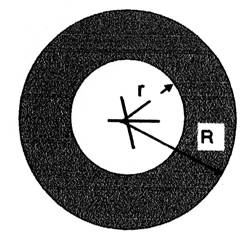
Figure 2
avec : R =
36,4 cm ; r = 17,2 cm |
4°
) Dans votre
établissement scolaire , 28 élèves ont été
reçus au CAP sur 40 présentés.
Quel
est le pourcentage de réussite ?
|
SOS cours |
5°) Calculer :
|
SOS cours |
|
a
) 2,63 + 6,2 ( 5,34 - 3,174 ) = x1 |
|
|
b) ( 12,56 +6,37 ) x 4,05
+ 6,39 = x2 |
|
6°)
|
SOS
cours |
||
|
|
||
|
|
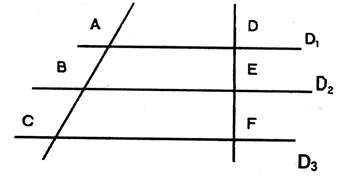
D1 ; D2 ; D3 sont // AB = 18 mm ; BC
= 14 mm ; DE = 13,5 mm Calculer
la longueur DF |
|
7°) Résoudre les équations suivantes :
|
SOS
cours |
|
2 x
-3 = 7 |
|
|
3 x
+ 2 = 8 |
|
|
6 x
+ 1 = 11 |
|
|
2,3
x + 1,3 = 5,9 |
|
|
1,5
x - 4,2 = 7,2 |
|
|
4 x
- 3 = 2 x
+ 5 |
|
|
3 x
+ 2,3 = x - 1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8°) Calculer :
|
SOS cours |
|
( 32° 17’ 27’’ ) x 3 |
|
|
( 27° 17’ 20’’) : 3 |
|
|
42° 13’ 20’’ - 27°
12’’ |
|
|
42° 13’ 10’’ + 25°
57’ 27 ‘’ |
|
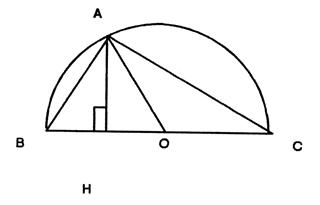
9°)
Dans un triangle ABC rectangle en A on donne AH = 28 et AO = 50.
|
SOS
cours (voir cas par cas) |
|
|
|
Calculer les mesures des cotés du triangle ABC. |
10° )
Exprimer en cm 3
|
SOS cours |
|
|
En cm 3 |
|
2,5
l |
|
|
3,2
dl |
|
|
4,7
hl |
|
|
6,7
dm3 |
|
|
12,5
cl |
|
|
13,4
ml |
|
11°) Exprimer en cl :
|
SOS cours |
|
|
C
L |
|
2,3 Ll |
|
|
4,5 dm3 |
|
|
4,3 cm3 |
|
|
12 mm3 |
|
|
5,7 daL |
|
|
3,4 L |
|
|
5 m3 |
|
|
17 m L |
|
|
8,3 dam3 |
|
12 ° ) Réduire au plus petit
dénominateur commun ( PPCM ) les fractions suivantes et calculer :
![]() ;
; ![]() et
et ![]()
|
SOS
cours |
Calculer :
S = ![]()
|
SOS cours (somme de
fractions de dénominateurs différents) |
13° ) Exprimer en m2 .
|
SOS cours |
|
0,37 km2 |
|
|
2,8 hm 2 |
|
|
45 dm2 |
|
|
8642 mm2 |
|
|
9643 cm2 |
|
|
10845 mm2 |
|
|
4 ha |
|
|
3 ares |
|
|
2 dam2 |
|
|
5 ha 3 ares |
|
|
17 ares 5 centiares |
|
14°
) Vous payez une bicyclette 1 147 € après avoir bénéficié d ‘
une remise de 7,5 % du prix marqué . Quel était le prix marqué ?
|
SOS
cours |
|
|
|
|
15°) Trois personnes A B et C ont gagné au loto la somme de 41 650 € qu ‘elles
vont se partager proportionnellement à leurs mises , respectivement 7€ , 28 € ; 84 € .
Calculer le
gain de A ,B et C.
|
SOS cours |
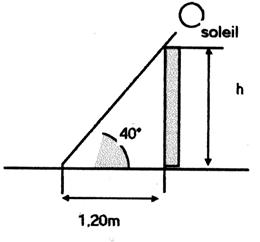
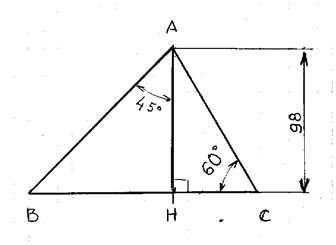
16 °) Calculer la hauteur h
|
SOS cours |
||
|
|
||
|
On a : 1 triangle
rectangle ; un angle la
longueur d'un coté: Nous
avons recours aux relations trigonométriques. |
|
|
17 ° ) Soit un
repère cartésien et les trois points :
|
SOS cours |
|
A ( 2 ; 3 ) ; B ((-3 ;0
) ; C ( (4 ; -1 ) . Donner
les cordonnées de tous les points
situés à l’intérieur du triangle ABC et dont l’abscisse et l’ordonnée sont
des entiers. ( faire le graphique ). |
|
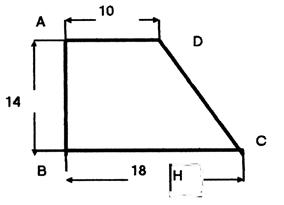
18 ° ) On considère
le trapèze ABCD . Calculer AC ; BD ;
CD .
|
SOS cours voir cas par cas |
|
|
|
|
19° ) Calculer :
|
|
|
|
|
|
7 % de 5 000€
|
|
8 % de 4500 € |
|
|
; 11% de 864 € |
|
9.2 % de 7250 € |
|
|
SOS
cours |
20°) Une pyramide régulière a pour base un carré
de coté « c » et pour hauteur « h ».
Calculer son volume dans le cas où c= 17 cm et h = 34 cm.
|
SOS cours |
21°) Compléter le tableau.
|
SOS
cours (voir
colonne par colonne ) |
|
|
n |
n2 |
n3 |
|
|
6,25 |
|
|
|
|
|
121 |
|
|
|
|
410,0625 |
|
4,5 |
22 °) On considère
la droite passant par l’origine O d’un repère cartésien et par le point A ( -2 ; 5 ) De quelle équation de la fonction
linéaire est - elle la représentation graphique ?
|
SOS cours |
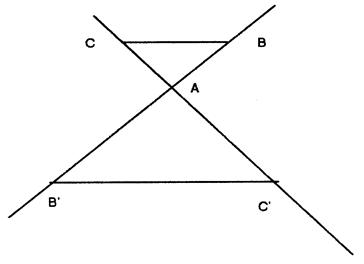
23 °) Dans la figure ci - dessous, comparer les
triangles :
ABC et A B’C’
;
(BC) // ( B’C’ )
|
SOS cours |
|
|
|
BC
= 2,8 cm ; B’C’ = 4 cm ; AC = 2
cm ; rectangle en A |
24
° ) Représenter graphiquement les fonctions
« f » et « g » définies par :
f :
x ![]() - 6 x ;
g : x
- 6 x ;
g : x ![]()
![]() x ; h : x
x ; h : x ![]() x ²
x ²
|
SOS cours |
25 ° ) Le prix d’un objet
est 4320€ ; celui-ci subit une augmentation de 9% .Calculer le
nouveau prix .
|
SOS
cours |
26 °) Exprimer en ………….
|
SOS cours |
|
Exprimer en m : |
|
|
3 dm |
|
|
5 cm |
|
|
34 hm |
|
|
2,6 dam |
|
|
124 mm |
|
|
2,46 km |
|
|
Exprimer en dm : |
|
|
2,5 m |
|
|
4,3 km |
|
|
5,66 cm |
|
|
123 dam |
|
|
1243 mm |
|
|
37,6 hm. |
|
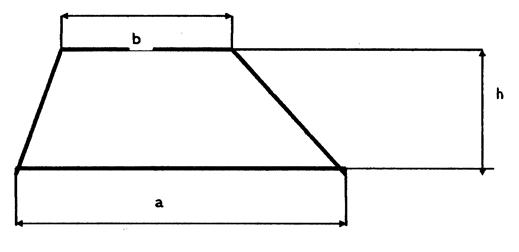
27 ° ) Compléter le tableau : A = aire du trapèze.
|
SOS cours |
|
|
Les transformations
d'égalités |
|
A |
756 |
|
8643 |
|
275 |
mm² |
|
a |
|
47 |
554 |
756 |
17 |
mm |
|
b |
20 |
31 |
|
222 |
5 |
mm |
|
h |
12 |
24,2 |
24,7 |
67,4 |
|
mm |
|
|
|
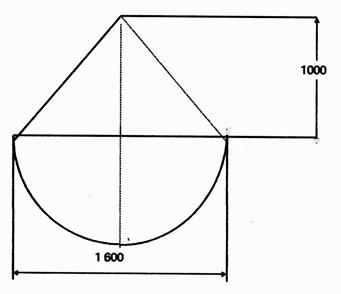
28°
) Etant donné le schéma représentant un flotteur composé d ’une demi - sphère surmontée
d’un cône , calculer le volume du flotteur .
|
|
|
|
SOS cours |
29 ° ) Calculer : AB et AC:
|
|
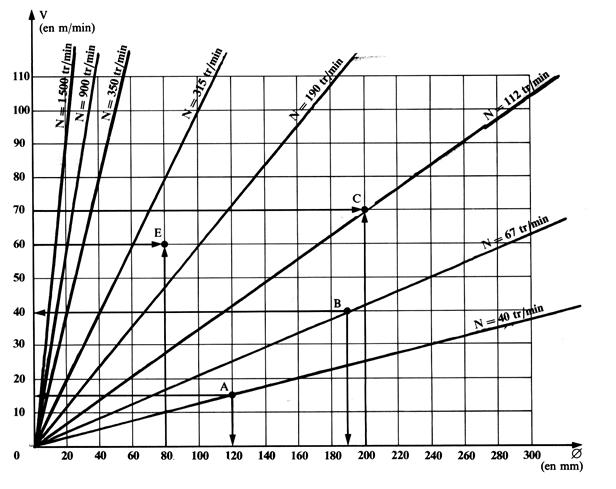
30°) En utilisant
l ‘[WR.1] abaque de
fraiseuse ci - dessous :
a ) Quelle vitesse de rotation
« n » en tours / min. Doit-on utiliser avec une fraise de 125 mm de diamètre
et une vitesse de coupe de 40 m / min .
b ) La vitesse de coupe étant de 90 m / min ;
la fraise a pour diamètre 150 mm A
quelle vitesse ( dit aussi
« fréquence ») de rotation doit régler la machine ?
|
|
Info : la vitesse de coupe est obtenue expérimentalement dans un
laboratoire . On usine une pièce dont la
matière est connue.
La vitesse de coupe retenue est
celle qui a permis de faire la plus grande quantité de copeaux entre deux
affûtages d’outil .
Remarque V = 2 ( N
|
|
31°)
Un couple a pris rendez-vous avec son
banquier afin d’étudier l’aspect financier de l’achat d’un pavillon.
Le
prix de la maison est de 700 000 € auquel il faut ajouter 4,5 % de
frais de notaire.
Calculer le coût d’achat de la maison .
32°) Dessiner , coter et citer
les caractéristiques (et propriétés) des figures
géométriques planes élémentaires .
suivantes :
Parallélogramme
, carré , rectangle
, losange , trapèze , triangles ( rectangle , isocèle , équilatéral ;scalène
)
Faire
un tableau !!!!
|
|
Fin de la
série.