Devoir sommatif

[R1] [R2] [R3] [R4]

Devoir sommatif niveau V / CORRIGE[R5] [R6] [R7]

1 °) Ranger les nombres suivants par ordre de grandeur croissante :

SOS cours

15,006 ; 15,016 ; 15,061 ; 15,601 ; 15,106

15,006 ;

15,016

15,061

15,106

15, 601

SOS cours

2°) Exprimer en heures ,minutes , secondes :

temps

4730 s

4730:3600 =1h

4730-3600 =1130:60=18 mn

0,8333333fois60 = 50 s

1803 s

1803:60=30mn

3 s

85 450 s

23h

2650s = 44 mn

10 s

Réponse : 2 possibilités : la calculatrice ou manuellement

« Manuellement » : faire la division par « 60 »

SOS cours

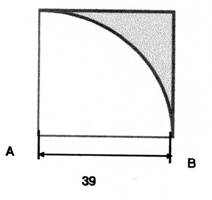
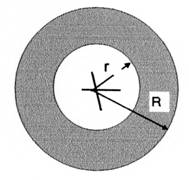
3°) Calculer l’aire des surfaces ombrées :

Figure 1 :

Figure 2

Corrigé :figure 1

Faire l'aire du "carré" moins l'aire du "quart de cercle":

1) Aire du carré = 39 fois39 = 1521

2) aire du 1/4 de cercle

3,14 fois 39 fois 39 divisé par 4 =1193,985

3) Aire de la zone grise = 1521 - 1193,985 = 327, 015

avec : R = 36,4 cm ; r = 17,2 cm

Corrigé figure 2

Aire de la couronne est égale à la différence de l'aire du disque de rayon "R" avec l'aire du disque de rayon "r"

L'aire du disque de rayon "R"

3,14 fois 36,4 fois 36,4 = 1324,96

L'aire du disque de rayon "r"

3,14 fois 17,2 fois 17,2 = 918,136

Aire de la couronne :

1324,96-918,136 = 406,824 cm²

SOS cours

4° ) Dans votre établissement scolaire , 28 élèves ont été reçus au CAP sur 40 présentés.

Quel est le pourcentage de réussite ?

On pose la relation mathématique : x = y

On appelle X le nombre d'élèves qui se sont présentés à l'examen 40

On appelle y le nombre d'élèves reçus

On remplace dans le relation de départ:

fois 40 = 28 ;

Je cherche "a"

a = 28 fois 100 divisé par 40

a=70

Conclusion : 70% des élèves ont été reçus à l'examen

SOS cours

5°) Calculer :

a ) 2,63 + 6,2 ( 5,34 - 3,174 ) = x₁

2,63 + 6,2 fois 2,166 =2,63+13,4292

x₁ = 16,0592

b) ( 12,56 +6,37 ) x 4,05 + 6,39 =x₂

x₂= 83,0565

SOS cours

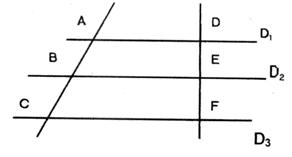
°) D₁ ; D ₂ ; D ₃sont //

AB = 18 mm ; BC = 14 mm ; DE = 13,5 mm

Calculer la longueur DF

Relation mathématique:

== ;

On remplace dans les relations les lettres par les valeurs données:

= =

On établit deux proportions , dans les quelles on connaît 3 valeurs sur quatre

1°) =

On calcule la quatrième proportionnelle: EF = (14 f ofois is 13,5 ,5) divisé 18

EF = 10,5

2°) =

On calcule la quatrième proportionnelle DF = (32 fois 13,5)divisé par 18

DF = 24

SOS cours

7°) Résoudre les équations suivantes :

2x -3 = 7

x =5

3x + 2 = 8

x =2

6x + 1 = 11

x =2

2,3 x + 1,3 = 5,9

x =2

1,5 x - 4,2 = 7,2

x =7,6

4x - 3 = 2x + 5

x = 4

3x + 2,3 = x - 1,2

x =-1,75

= 5

x = 17

= 2

x = 6

= 6,3

x = 16,7

+3 = 5

x = 4

+ 1,2 = 3,1

x = 5,7

- 4 = 0,2

x = 21

+ 4 = 2 x - 10

x = 8

8°) Calculer :

SOS cours

( 32° 17’ 27’’ ) x 3

96° 51' 81'' = 96° 52' 21''

( 27° 17’ 20’’) : 3

9° 5' 46,66''

42° 13’ 20’’ - 27° 12’’

15° 1' 20''

42° 13’ 10’’ + 25° 57’ 27 ‘’

67° 70' 37'' = 68° 10' 37''

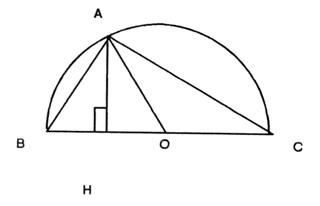
9°) Dans un triangle ABC rectangle en A on donne AH = 28 et AO = 50.

Calculer les mesures des cotés du triangle ABC.

SOS cours (voir cas par cas)

Il faut donc trouver les longueurs des cotés: AB ; BC ; CA :

après avoir identifié ce que l'on a et ce que l'on sait sur le cercle et le triangle inscrit ; (si le pont "O" centre du cercle inscrit , point d'intersection des médianes d'un triangle ) ABC est un triangle rectangle

1°) CALCUL de BC :

Commentaire : AO est égal au rayon du cercle = 50

AO = BO = OC = 50 ; donc BC =100

SOS CHALES

2° )calcul de AC (dans le triangle AHC )

a) On connaît AH et AO , AHO est un triangle rectangle , nous pouvons calculer OH

AO² = AH² + HO²

Donc HO² = AO² - AH²

(puissances opérations par Pythagore )

Calcul de OH=

OH =

OH = 41,4

SOS PYTHAGORE

b) On peut calculer HC :

HC = HO + OC

HC = 41,4 + 50

HC = 91,4

Nous connaissons AH et HC nous pouvons calculer AC

AC² = AH² + HC² (SOS CHALES)

AC² = 28² + 91,4²

AC² =8353,96 +784

AC² =9137,96

AC =

AC = 95,5

SOS PYTHAGORE

SOS : Arrondir : ?

CALCUL de BA:

On sait que BC² = BA² +AC²

BA² = BC²- AC²

On connaît : BC ( = 100 ) et AC (= 95,5)

On remplace dans l'égalité ci-dessus :

BA² = 100²- 95,5²

BA² = 10 000 - 9120,25

BA² = 879,75

BA = 29,7

10° ) Exprimer en cm ³

cm ³ SOS cours

2,5 litres

2500

3,2 dl

320

4,7 hl

470000

6,7 dm³

6700

12,5 cl

125

13,4 ml

13,4

11°) Exprimer en cl :

Clitre SOS cours

2,3 l

230

4,5 dm³

450

4,3 cm³

0,43

12 mm³

0,0012

5,7 dal

5700

3,4 l

340

5 m³

500 000

17 ml

1,7

8,3 dam³

8300000000

SOS cours

12 ° )Réduire au plus petit dénominateur commun ( PPCM ) les fractions suivantes et calculer :

; et

On décompose les 3 nombres en produit de nombres premiers:

12 = 2₁ 2₂ 3₁

9 = 3₁ 3₂

15 =3₁5₁

PPCM de (12;9;15) = 2₁ 2₂ 3₁ 3₂5₁

Calcul : 2 2 3 35 =180

Conclusion: le PPCM de ( 12;9;15) est de 180

SOS cours (somme de fractions de dénominateurs différents)

Calculer : S = + -

S = + - ;

il faut réduire les trois fractions au même dénominateur :

S = + -

13° ) Exprimer en m².

SOS cours

0,37 km²

37 000 m²

2,8 hm ²

28 000 m²

45 dm²

0,45 m²

8642 mm²

0,008642 m²

9643 cm²

96,43 m²

10845 mm²

1,1845 m²

4 ha

40 000 m²

3 ares

300 m²

2 dam²

200 m²

5 ha 3 ares

50300 m²

17 ares 5 centiares

1705 m²

14° ) Vous payez une bicyclette 1 147 € après avoir bénéficié d ‘ une remise de 7,5 % du prix marqué . Quel était le prix marqué ?

OS cours

Il faut choisir entre 3 modèles mathématique; un seul convient:

y = x

Y = () x

Le modèle qui convient est :

Y = () x

On sait que "a"= 7,5 ; que "y" (prix après réduction) =1147

On remplace dans la formule:

1147 = x

1147 = 92,5 x

x =

x = 1240

Conclusion :

le prix de départ est de 1240 Francseuros

15°) Trois personnes A B et C ont gagné au loto la somme de 41 650 € qu ‘elles vont se partager proportionnellement à leurs mises , respectivement 7 € , 28 € ; 84 €.

Calculer le gain de A ,B et C.

SOS cours

Nous devons connaître le total des mises :

7 + 28 + 84 = 119 €

pour une mise de 119 € il a été gagnée la somme de 41650 € .

gain

Pour une mise de:

Pour "A"

Pour "B"

Pour "C"

total

41 650

119

Calcul des gains de "A"

= ;

A = 2450 € €

Calcul des gains de "B"

= ; B = 9 800 €

Calcul des gains de "C"

== ; C = 29 400 €

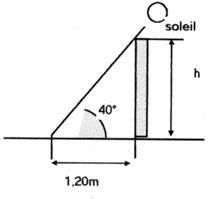
16 °) Calculer la hauteur h

SOS cours

On a : 1 triangle rectangle ; un angle ,la longueur d'un coté:

Nous avons recours aux relations trigonométriques.

Tan 40° =

Voir tableau : tan 40° =

h = tan 40° 1,20

h = 1,007 m

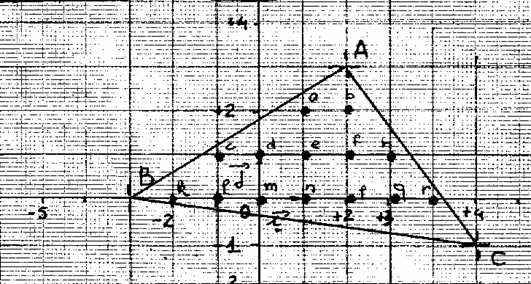
17 ° )Soit un repère cartésien et les trois points : SOS cours

Il y a 14 points dans le triangle ABC , don l' abscisse et l'ordonnée est un nombre entier

A ( 2 ; 3 ) ; B ((-3 ;0 ) ; C ( (4 ; -1 ) . Donner les cordonnées de tous les points situés à l’intérieur du triangle ABC et dont l’abscisse et l’ ordonnée sont des entiers. (faire le graphique ).

SOS cours voir cas par cas

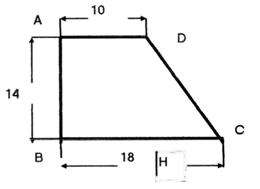
18 ° ) On considère le trapèze ABCD . Calculer AC ; BD ; CD .

Calcul de AC:

Commentaire: AC est l'hypoténuse du triangle rectangle ABC

D'après Pythagore

AC² = AB² + BC²

AC² = 14² + 18²

AC =22,8

Pythagore: SOS PYTHAGORE

Calcul de BD(trait bleu)

Commentaire: BD est l'hypoténuse du triangle rectangle BAD

D'après Pythagore

BD² = AB² + AD²

BD² = 14² + 10²

BD =17,2

Calcul de CD: (trait vert)

Commentaire: CD est l'hypoténuse du triangle rectangle DHC

D'après Pythagore

DC² = DH² + HC²

Calcul de HC = 18 - 10 = 8

DC² = 14² + 8²

BD =16,1

19° ) Calculer :

7 % de 5 000F ; 11% de 864 F ; ,8 % de 4500 F ;9.2 % de 7250 F

SOS cours

Il faut choisir entre 3 modèles mathématique; un seul convient:

y = x ou Y = () x ou Y = () x

Le modèle qui convient est :

y = x

CALCUL de 7 % de 5 000 €

On sait que "a"= 7 ; que "x" (prix =5 000 € )

On remplace dans la formule:

Y = 5 000

Y = 350

Conclusion : 7% de 5 000 F = 350 €

CALCUL de 11 % de 864€

On sait que "a"= 11 ;

Et que "x" (prix = 864 € )

On remplace dans la formule:

Y = 864

Y = 95,04

Conclusion : 11% de 864 F = 95,04 €

CALCUL de 6,8 % de 4 500€

On sait que "a"= 6,8 ;

Et que "x" (prix =4 500 € )

On remplace dans la formule:

Y = 4500

Y = 306

Conclusion : 6,8% de 4 500 F€ = 306 F€

CALCUL de 9,2 % de 7 250F €

On sait que "a"= 9,2 ;

Et que "x" (prix =7 250 F€ )

On remplace dans la formule:

Y = 7250

Y = 667

Conclusion : 9,2% de 7250 F€ = 667 F€

20°) Une pyramide régulière a pour base un carré de coté « c » et pour hauteur « h ».

Calculer son volume dans le cas où c= 17 cm et h = 34 cm.

SOS cours

Volume de la pyramide : = ( surface de base hauteur)divisé 3

Formule:

Calcul de l'aire de base:

cc =17² (cm¹)² = 289 cm²

Calcul du volume:

B = 289cm² ; H =34cm

(B h = 289 cm²34 cm¹=…cm³)

V = = 3275,3

Conclusion : le volume de la pyramide est de 3275,3 cm3

21°) Compléter le tableau.

SOS cours (voir colonne par colonne )

n²

n³

6,25

39,0625

244,14063

2,5

121

1331

3,316

20,25

410,0625

8293,5141

4,5

SOS cours

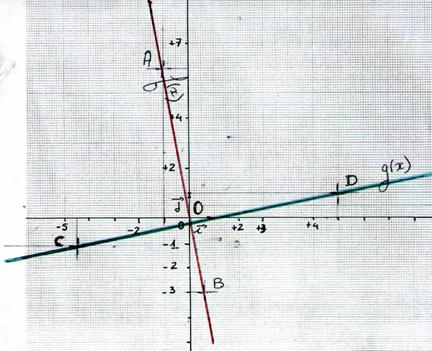
22 ° ) On considère la droite passant par l’origine O d’un repère cartésien et par le point A ( -2 ; 5 ) De quelle équation de la fonction linéaire est - elle la représentation graphique ?

SOS cours

L'équation de la fonction linéaire est de la forme : y = ax

A ( -2 ; 5 ) ; se souvenir A ( x_A ; y_A )

Avec

x_A=abscisse du point A

et y_A= ordonnée du point A

Il suffit de trouver la valeur de "a" et l'intégrer dans le modèle :

Calcul de "a" = ;

Pour A : y_A = 5 ; x_A= -2 ; on applique

a = ~~= -~~=2,5 – 2,5

Conclusion : l'équation est: y = -2,5 x

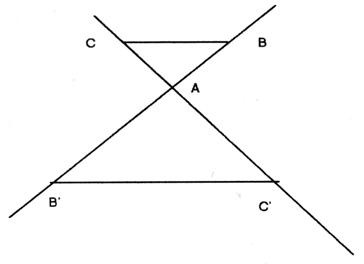
23 °) Dans la figure ci - dessous , comparer les triangles :

ABC et A B’C’ ; (BC ) // ( B’C’ )

B’

C’

BC = 2,8 cm ; B’C’ = 4 cm ; AC = 2 cm ; rectangle en A

Calculer AB ; AB’ ; AC’

SOS cours (voir les triangles homothétiques )

SOS

Transformer le dessin :

Faire une rotation dans le sens des aiguilles d'une montre autour du point A; pour obtenir BC // B'C' ( le point B doit se trouver sur le segment B'A )

Constat : les triangles ABC et AB'C' sont homothétiques ; il existe donc un rapport d' homothétie :

On prend deux rapports donc on connaît 3 valeurs sur 4

= ;

= , voir le produit en croix

Nous connaissons AC' = 2,86 ;

et B'C'= 4 , le triangle est rectangle en A

Nous pouvons chercher AB' par Pythagore:

(B'C')² = (B'A)²+ (AC')²

4² = (B'A)²+ (2,86)²

après transformation:

4² - (2,86)² = (B'A)²

ou (B'A)² = 4² - (2,86)²

(B'A)² = 16 -8,1796

(B'A)² =7,8204

B'A = 2,7964978

B'A = 2,80 à 0,01 prés

On peut maintenant calculer la valeur de AB : à partir des rapports précédemment établis :

On remplace dans les rapports les valeurs que l'on nous donne.

=_;=_;=

ainsi:! =

AB = (2,8 fois 2,8)divisé par 4

AB = 1,96

Les rapports homothétie sont (ils n'y a pas d'ordre ) ==

On remplace dans les rapports les valeurs que l'on nous donne.

AC' = (4 fois 2 ) divisé par 2,8

AC' (2,8571429 (voir "arrondir" )

24 ° ) Représenter graphiquement les fonctions « f » et « g » définies par :

SOS cours

f : x -6x ; g : x x

Pour représenter graphiquement les deux fonctions il faut pour chacune d'elles établir un tableau de variation (appelé : tableau de proportionnalité pour la fonction linéaire ) dans lequel on cherchera les coordonnées de trois points ( 2 pour tracer la droite , le troisième pour vérifier si la droite est bien tracée )

f : x -6x

Point A

Point O

Point B

Pour "x" =

-1

0,5

y = -6 fois x

-1 fois -6 = +6

-3

Pour g : x x

Tableau :

Point C

Point O

Point D

Pour "x" =

-4,5

4,5

y = fois x

fois -4,5 = -1

25 ° ) Le prix d’un objet est 4320F ; celui-ci subit une augmentation de 9% .Calculer le nouveau prix .

SOS cours

Deux solutions sont permises(voir cours SOS)

Solution proposée :

On applique la formule suivante :

(à connaître)

y = ( ) x

Résolution:

On pose

x = 4320

a = 9

On remplace les lettres par les valeurs retenues: ce qui donne

y = ( ) 4320

y = 1,09 fois 4320

y = 4708,8

conclusion: le nouveau prix est de 4708,8 €

26 °) Exprimer en ………….

SOS cours

Exprimer en m :

3 dm

0, 3 m

5 cm

0,05 m

34 hm

3 400 m

2,6 dam

26 m

124 mm

0,142 m

2,46 km

2 560 m

exprimer en dm :

2,5 m

25 dm

4,3 km

43 000 dm

5,66 cm

0,566 dm

123 dam

12 300 dm

1243 mm

12,43 dm

37,6 hm.

37 600 dm

27 ° ) Compléter le tableau : A = aire du trapèze.

SOS cours

Les transformations d'égalités

756

943,8

8643

32 958,6

275

mm2

= 106

554

756

141,83

222

24,2

24,7

67,4

28° ) Etant donné le schéma représentant un flotteur composé d ’une demi - sphère surmontée d’un cône , calculer le volume du flotteur .

SOS cours

Nous avons besoin des formules concernant le volume d'une sphère (on divisera par 2 pour avoir le volume de la demi sphère) et de la formule du cône :

( avec pi = 3,14)

Formule du volume d'une sphère:

V =

Formule du volume du cône :

V =

Il faut faire la somme des deux volumes:

Calcul du volume de la sphère:

V = ; R = 1600 / 2 = 800

V =

V _sphère= 2,1435733 10⁹

Calcul du volume de la 1/2 sphère:

1,07177867 10⁹

volume du cône :

V =

V _cône= 6,698666710⁸

Volume totale: V _1/2sphère+ V _cône

10,7177867 10⁸+6,698666710⁸= 17,416453410⁸

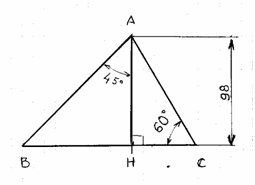
29 ° ) Calculer : AB et AC:

SOS cours (voir cas par cas)

Calcul de AB: il y a deux solutions

Première solution: Pythagore

AB² = BH² + HA²

Comme le triangle ABH est un demi carré; (on peut aussi un triangle isocèle particulier); on en déduit que les coté formant l'angle droit on la même mesure soit "98" : donc BH =HA = 98

On peut écrire que :

AB² = 98² + 98² ( = 2 a²)

AB² =9604 +9604

AB² =19208

AB = ; ( = a )

AB (138,59293

Deuxième solution:

On applique la formule : la diagonale du carré est égale à : " a " "a" étant la longueur d'un coté formant l'angle droit

On prendra : = 1,414

Donc : AB = 1,414 98

AB = 138,572

SOS cours (voir cas par cas)

Voir aussi :les caractéristiques d'un demi triangle équilatéral

Calcul de AC:

Dans un triangle rectangle dont on ne connaît que la longueur d'un coté (98) et un angle(60° et par déduction 30° ) , la recherche des longueurs ne peut se faire qu'en utilisant les relations trigonométriques:

30° )En utilisant l ‘[WR.8] abaque de fraiseuse ci - dessous , quelle vitesse de rotation « n » en tours / min. Doit-on utiliser avec une fraise de 125 mm de diamètre et une vitesse de coupe de 40 m / min .

SOS cours