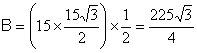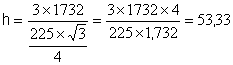|
Auteur :
WARME R. ( revu : le 28/09/06)
INFORMATIONS sur
|
||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|
ETABLISSEMENT :
………………………………………….. |
||
En
RESUME : (niv V)
Notion
de volume. — Tout
solide occupe une portion déterminée de l’espace appelée « volume de ce
solide ».
L’égalité
de deux volumes, les diverses opérations sur les volumes se définissent comme
cela a été fait pour les surfaces planes. Ainsi, le volume du polyèdre obtenu après
juxtaposition de deux polyèdres donnés et suppression de la portion de face
commune est, par définition, la somme des volumes de ces deux polyèdres. Cette
juxtaposition peut se réaliser d’une infinité de façons et les divers polyèdres
ainsi obtenus ne sont pas égaux, mais ont même volume, ils sont dits
équivalents.
Deux polyèdres équivalents sont deux polyèdres
qui ont même volume.
Unité
de volume. — Les
volumes sont donc des grandeurs mesurables.
On
choisit pour unité de volume le volume du cube ayant pour arête l’unité de
longueur.
A chaque
unité de longueur correspond ainsi une unité de volume. L’unité principale de
volume est le mètre cube (m3); on peut aussi utiliser le décimètre
cube (dm3), le centimètre cube (cm3), etc.
Dans les
énoncés relatifs aux mesures des volumes nous conviendrons que
1°) Toutes les longueurs sont mesurées avec la même
unité. (dans un calcul il faut
« homogénéiser » les dimensions , Càd les
exprimer dans la même unité de mesure)
2°) Les surfaces et les volumes sont mesurés avec
les unités de surface et de volume correspondant à l’unité de longueur adoptée.
Il
n’existe pas de mot pour désigner la mesure d’un volume ( tel que le mot « aire » pour
la mesure d’une surface). Nous conviendrons, dans ce qui suit, que l’expression
« volume d’un solide désigne en réalité la mesure de son volume de même
que tout « segment» désigne la mesure de ce segment.
On
retiendra le Théorème suivant
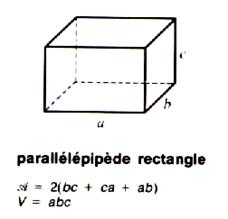
Le
volume d’un parallélépipède rectangle est égal au produit de ses trois
dimensions.
|
Leçon |
Titre |
|
|
N°19 |
GEOMETRIE ESPACE et "AIRE et VOLUME de solides usuels" |
|
|
CHAPITRES |
:Info + Cd |
|
|
I )
Les Unités de volume : le mètre cube ( solide ) et le litre ( liquide). |
||
|
II )Les
conversions : de « litre »
Þ en « cube » ; de « cube »Þ en
« litre » . |
||
|
|
||
|
1°) description |
||
|
2°) représentation en
perspective cavalière . |
||
|
3°) développement |
||
|
4°) Aire et volume. |
||
|
|
||
|
1°) description |
||
|
2°) représentation en
perspective cavalière . |
||
|
3°) développement |
||
|
4°) Aire et volume. |
||
|
|
||
|
1°) description |
||
|
2°) représentation en
perspective cavalière . |
||
|
3°) développement |
||
|
4°) Aire et volume. |
||
Dictionnaire : voir la définition de parallélépipède , parallélépipédique ,
i : Les deux unités de mesure de volume à
connaître sont : le mètre cube (ses
multiples et ses sous multiples) utilisé pour mesurer les volumes des
solides et le litre unité
utilisé pour mesurer les volumes des liquides , ou matière en poudre ou
granulée ( farine , les céréales……) .
Lire : « m » pour « mètre »
a) L'unité principale est le « mètre cube » : symbole m 3 Lire : Exposant « 3 » ,ou puissance « 3 » ou « au cube »
( le mètre cube est un cube de 1 mètre
de côté ) 
D’autres unités sont utilisées dans la vie
courante sont les sous multiples :
le décimètre cube : dm3 (c'est
un cube de 1 dm d'arête)
le centimètre cube : cm3
(c'est un cube de 1 cm
d'arête)
le millimètre cube : mm3
(c'est un cube de 1 mm
d'arête)
1b ) L’unité de capacité :
les mesures de capacités sont utilisées pour mesurer des
volumes occupés par les liquides.
L'unité de capacité est le
litre ; c'est le volume occupé par 1 kilogramme d'eau pure à son maximum de densité. Le litre correspond
au volume occupé par un cube de un
décimètre de côté .
1 mètre cube vaut donc 1 000
litres .(ou 1 kilolitre)
il faut savoir que 1 décimètre cube ( dm3) contient un volume
équivalent à 1 litre d’eau pur à 4° Centigrade .
· mesures
équivalentes :
1dm3 = 1 l ; Un litre = 100 cl ; 100 cl = 1 dm3 = 1000 cm3 donc 1cl
= 10 cm3
et 1m3 = 1000
dm3 = 1 000
litres .
i
les 2
unités de base utilisées
au quotidien sont :
|
B ) Le
décimètre cube : (
symbole : dm3 ) et le
litre ( l ) |
iDans la vie quotidienne : contenance de matériel de cuisine ( verre
, bouteille , flacon ) , dans les recettes de cuisine ( mélange , et proportion
de liquide et solide ) , dans le commerce des produits liquides ( sauce
,boissons, parfum ou autres liquides ),
, on utilise couramment et indifféremment le décimètre cube et ses sous
multiples ( le centimètre cube et le
millimètre cube ) et le litre et ses
sous multiples ( décilitre , centilitre , millilitre ).
Souvent il est nécessaire de savoir
passer de l’une à l’autre de ces unités ( on dit « convertir » ) , au risque de ne pas
réussir soit une recette ,soit un achat et donc d’être mécontent .
Voir i Cd
sur le : « Décimètre » et le « cube »
=Ci dessous nous montrons que le
« décimètre cube » contient 1000 cubes ayant chacun 1 cm d'arête .
|
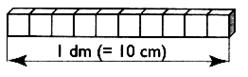
A) Soit un cube de 1 cm de
côté . |
|
|
B) 10 cubes de 1cm d'arête forment
une barrette de 1 dm de longueur. ( 10 cm = 1dm) |
|
|
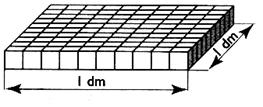
C ) 10 barrettes
forment une plaque carré de 1 dm de côté . Cette plaque contient 100
cubes de 1 cm d'arête. |
|
|
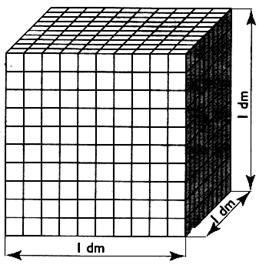
D ) 10 plaques de 1cm d'épaisseur , mesure un
décimètre de hauteur. Ces 10 plaques contiennent
chacune 100 cubes de 1 cm d'arête. Le cube de 1 dm d'arête
contient donc 10 fois 100 cubes de 1cm cube . soit
1000 cm cube. Donc : 1 dm 3 =
1 000 cm3 |
|
En utilisant la
démonstration ci dessus nous pourrions montrer ainsi que 1 cm3
contient 1000 cubes de 1 mm
de côté.
(
1 cm3
= 1000 mm3 )
Avec
les exemples précédents , il nous
est possible d'obtenir ce tableau :
|
Symbole |
Correspondance en m3 en
valeur décimale et sous forme de puissance de 10 |
|
|
Kilomètre cube |
km3 ( = 1000m)3 |
1 km3 =1 000 000 000 m3 = 1 ´ 10 9 m3 |
|
Hectomètre cube |
h m3 ( = 100m)3 |
1 h m3 = 1 000 000 m3
= 1 ´ 10 6 m3 |
|
Décamètre cube |
da m3 ( = 10m)3 |
1da m3 = 1 000 m3 = 1 ´ 10 3 m3 |
|
Mètre cube |
m3 ( = 1m)3 |
1 m3 = 1´ 10 0 m3 |
|
Décimètre cube |
d m3 ( = 0,1m)3 |
1 d m3 =
0 , 001 m3 = 1 ´ 10 -3 m3 |
|
Centimètre cube |
c m3 ( = 0,01m)3 |
1 c m3 =
0, 000 001 m3 = 1 ´ 10 -6 m3 |
|
Millimètre cube |
m m3 ( = 0,001m)3 |
1 m m3 = 0 , 000 000 001m3 =
1 ´
10-9 m3 |
( cliquer
ici : pour voir les unités de volume et
l'utilisation des puissances de dix)
Dans le cadre des calculs on
utilisera les puissances de dix , dans le cadre de
conversion on utilisera plus facilement le tableau de conversion ci dessous .
|
II )LE TABLEAU DE conversion . ( volumes et
capacité ) |
i Ci dessous est tracé le tableau qui permet d’effectuer les conversions des unités de volume couramment utilisées , tableau qu’il faut savoir construire sur feuille , et utiliser : Prendre une ligne par exercice !
|
km3 |
hm3 |
dam3 |
m3 |
dm3 |
cm3 |
mm3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
kl |
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
2 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Remarquez que chaque
colonne principale exprimée
en « cube » (exemple : dm3 ) est subdivisée en 3 sous
colonnes , les unités de capacité occupe une colonne , réparties de chaque côté de l’unité « litre »
, qui occupe la première sous- colonne des dm3
Pour les besoins de
compréhension ce cours vous propose deux La démarche
( I )
concernant l’explication de la
conversion avec un tableau dit
« simplifié » doit vous servir à comprendre le déplacement de la
virgule ,mais vous retiendrez la
démarche du chapitre II ( il faut savoir dessiner le tableau et énoncer la procédure de conversion ) .
|
II - 1 ) Première
démarche explicative sur la méthode de conversion en utilisant le tableau « non
simplifié » : |
œ |
A) Tableau de type
« non simplifié » : « à gauche » de la virgule se trouve l'unité choisie (ou
désignée) à droite de la virgule se trouve la partie décimale de l'unité
choisie ou désignée )
Pour
apprendre l’exploitation du tableau , on applique,
dans ce qui suit, la méthode utilisée
dans les conversions d’aire.
Ici une sous- colonne "virgule" sépare les « unités », dans cette colonne se déplace la virgule.
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
|
dm3 |
|
cm3 |
|
mm3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
B ) Procédure
permettant de transformer l '
unité de volume en multiples ou sous
multiples à partir d'une grandeur donnée. |
Exemple de conversion 32,24
dam3= ? ……..dm3
Pour remplir le tableau en vue de faire une
conversion il faut respecter la procédure
suivante:
1°) placer la virgule du
nombre donné sur le trait vertical "droit" de l'unité donnée.( da m3 , )
|
km3 |
|
hm3 |
|
dam3 |
, |
m3 |
|
dm3 |
|
cm3 |
|
mm3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2°) placer les chiffres du
nombre dans en respectant l ' ordre donné :
|
km3 |
|
hm3 |
|
dam3 |
, |
m3 |
|
dm3 |
|
cm3 |
|
mm3 |
|
||||||||||||||
|
|
|
|
|
|
0 |
0 |
3 |
2 |
2 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|||||||
i maintenant que la
"grandeur" est placée dans le tableau ,la conversion peut se faire
simplement:
3°) il faut déplacer le virgule ; la mettre sur le trait vertical
"droit" de l' unité "demandée " (d m3
, ) compléter de "zéros"
éventuellement !
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
|
dm3 |
, |
cm3 |
|
mm3 |
|
||||||||||||||
|
|
|
|
|
|
0 |
0 |
3 |
2 |
2 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|||||||
4° )
il suffit de reporter le
résultat , (lu sur le tableau )
32 , 24 dam
3 = 32 240 000 , 0 soit
32 240 000 dm3
remarque : la virgule est dite
« flottante » ;elle se trouve toujours sur le trait vertical
"limite droite" de l 'unité concernée.
|
II - 2 ) Procédure à retenir sur l ’
exploitation du tableau pour
effectuer une conversion: |
œ |
Dans le tableau type suivant , la virgule
se déplace sur le trait vertical
séparant les colonnes .
Exemple : faire la conversion 32,74
dam ² = …? ……..dm²
Solution
: il faudra
respecter l’ordre chronologique suivant :
Partie entière Partie décimale km3 hm3 dam3 m3 dm3 cm3 mm3
Reprise
de l’activité précédente :
Convertir 32 , 74 dam 3
en ….. dm3
procédure : Après avoir tracé le tableau :
1°) Placer la virgule sur le
trait vertical « droit » des dam 3
2°)
Placer les chiffres : 2 ; 3 ;
7 ; 4 (pour des raisons pratiques et
éviter des erreurs d’oubli il faut
placer les chiffres en partant de la virgule en allant de droite à gauche pour
la partie entière et de gauche à droite
pour la partie décimale )
3°) Remplir les cases vides
de « 0 »
4°) Déplacer la virgule sur le trait vertical
« droit » de l’unité demandée.
5°) Rendre compte .
|
km3 |
hm3 |
dam3 |
m3 |
dm3 |
cm3 |
mm3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
3 |
2 |
7 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
(3) |
(4) |
|
|
0 |
0 |
3 |
2 |
7 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Résultat :
Mais aussi :
32,74 dam 3 = 32
740 000 dm3 = 32 740 m3 = 0,032 74 hm3 = 32 740 000 000 000 mm3
= 32 740 000 000 cm3
Activités 1 :
1°) Placer
1 765 , 798
m3 ; 5,3 m3 ; 78 507 dm3 ; 2854 cm3 ; 5 832 mm3
dans le tableau ci
- dessous : ( tracer autant de lignes que
d’exercices de conversion )
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
|
dm3 |
|
Cm3 |
|
mm3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 765 , 798 m3 ; 5,3 m3 ; 78 507 dm3 ; 2854 cm3 ; 5 832 mm3
Activités 2 :
Convertir :
1 765 , 798
m3 en ………………………………dm3
5,3 m3 = ………………………..dm3
78 507 dm3 = ……………………m 3
2854 cm3 = ……………………m3
5 832 mm3 = …………………….cm3
Activité 3 : Convertir successivement : ( il suffit pour trouver les conversions
successives de déplacer la
virgule et de relever le résultat .
1 765 , 798 m3 en ………………………………dm3
1 765 ,
798 m3 en
………………………………dam3
5,3 m3 = ………………………..dm3 = ……………………cm3 ;
78 507 dm3 = ……………………m 3 = ……………………cm3;
2854 cm3 = ……………………m3 =……………….dm3
= …………….mm3 ;
5 832 mm3 =
…………………….cm3 =
……………………………….dm3
= Préambule « CAPACITE » :puisque 1 dm 3
est égal à 1 litre , nous mémoriserons
le tableau des valeurs équivalentes ci dessous :
|
dm3 |
cm3 |
mm3 |
||||||
|
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
|
B ) Mesure de capacité : |
=Instruments
de mesure :
a ) Les mesurent pour les liquides
|
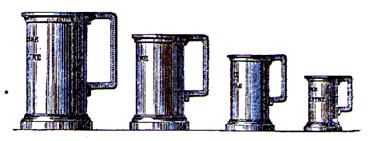
Les mesurent pour les
liquides sont en étain ; le cylindre a une hauteur double de son diamètre . Les dimensions du litre sont
« diamètre » : 86 millimètres ; hauteur :172 mm. |
|
b ) Les mesurent pour les matières sèches
|
Pour les matières sèches , telles que les grains , les mesures sont en bois
. La hauteur du cylindre est égale à son diamètre . La rafle
, est une planchette , elle sert à niveler , à retirer le surplus.
|
|
=Une
autre unité de volume est utilisée
pour mesurer des liquides . Cette unité de capacité
appelée : le
litre . 1 litre = 100 cl ( = 1 dm3
)
Le tableau de conversion :
|
kl |
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
Activités : pour vous amuser vous rechercherez les volumes donnés pour les récipients ci dessous ,
ensuite vous les convertissez
dans l’autre unité :
|
Nom
du récipient |
Donnez
les capacités en : l
; dl , cl , ml |
|
Exemple :
1Demi de bière |
0,25 l ; 2,5
dl ; 25 cl ; 250 ml |
|
Une
cuillerée à café |
|
|
Une
cuillerée à soupe |
|
|
Une
tasse à café |
|
|
Une
assiette à soupe |
|
|
Un bol
|
|
|
Une
brique de jus de fruit. |
|
|
Verre
à eau |
|
|
Verre
à vin |
|
|
Bouteille
de vin |
|
|
Bouteille
d’eau |
|
|
Flacon
de parfum |
|
|
Un
seau d’eau |
|
|
Une
baignoire |
|
|
Un cumuls d’eau chaude |
|
|
Un
réservoir de carburant. |
|
|
|
|
|
|
|
A vous de compléter le tableau
! ! !
puisque
1 l = 1 dm3 , nous
pouvons insérer le tableau précédent dans le tableau des
« volumes cubes»
|
m3 |
dm3 |
cm3 |
||||||
|
|
|
kl |
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
|
|
|
|
|
|
|
|
C) CONVERSIONS : passage
d’une capacité à un volume « prismatique » |
=
Puisque 1 dm 3 est
égal à 1 litre , nous mémoriserons le tableau
des équivalences ci dessous :
|
dm3 |
cm3 |
mm3 |
||||||
|
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
=
Activités : Reprendre les valeurs trouvées ci - dessus et pour vous amuser vous rechercherez les volumes donnés pour les récipients ci dessous ,
ensuite vous les convertissez
dans l’autre unité :
|
Nom du
récipient |
base
le dm3 = ….. cm3= ……. m m3 |
Capacité : L ;
dl , cl , ml |
|
Exemple : 1Demi de bière |
=
0,25 dm3 ; 250 cm3 ,
250 000 m m3 |
0,25 l ; 2,5 dl ;25
cl ; 250 ml |
|
Une
cuillerée à café |
|
|
|
Une
cuillerée à soupe |
|
|
|
Une
tasse à café |
|
|
|
Une
assiette à soupe |
|
|
|
Un bol
|
|
|
|
Une
brique de jus de fruit. |
|
|
|
Verre
à eau |
|
|
|
Verre
à vin |
|
|
|
Bouteille
de vin |
|
|
|
Bouteille
d’eau |
|
|
|
Flacon
de parfum |
|
|
|
Un
seau d’eau |
|
|
|
Une
baignoire |
|
|
|
Un cumuls d’eau chaude |
|
|
|
Un
réservoir de carburant. |
|
|
|
|
|
|
|
|
|
|
=Le tableau suivant doit être
mémorisé : ( attention : puissance
« 3 » ; 3 sous colonnes par unité considérée)
|
km3 |
hm3 |
dam3 |
m3 |
dm3 |
cm3 |
mm3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
kl |
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
Remarques :
conversions à savoir
faire mentalement .
1 litre =
10 dl = 100 cl = 1000ml = 1 dm3
= 1000 cm3
1 dl = 0,1 l = 100 cm3 = 10
cl = 100 ml ; ……
1cl = …….l = …… cm3 =
……….dl = …………. ml .
Il faut savoir reproduire le tableau ci dessous ( d’abord sur papier ; puis mentalement )
Les
corrigé sont à la fin du cours .
|
III ) LES 3 SOLIDES
USUELS : CUBE ;
PARALLELEPIPEDE RECTANGLE ; CYLINDRE . |
|
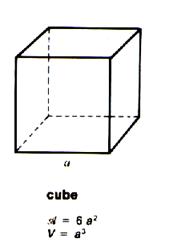
1°) description du cube . |
Les faces :
6 faces carrées : Les faces opposées sont parallèles deux à deux et les
faces ayant une arête commune sont perpendiculaires .
Chaque face étant un carré , les arêtes
opposées d'une face sont parallèles .
|
|
|
|
Les arêtes : Il possède 12 arêtes de même longueur . Les arêtes aboutissant à un même sommet sont
perpendiculaires deux à deux . |
|
Les sommets :
|
Il a 8 sommets. * 3 arêtes aboutissent à
chaque sommet . |
|
|
2° )
représentation du cube en perspective cavalière . |
Exemple: de représentation en perspective d'un cube
|
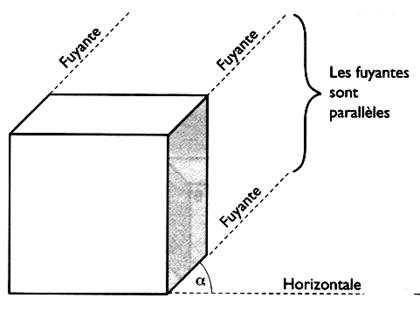
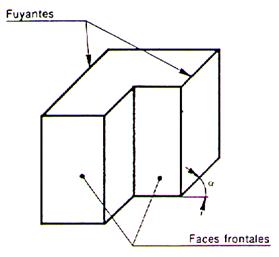
INFORMATION
sur la Perspective
cavalière : |
(en perspective cavalière la « vue de
face » est en vraie grandeur) |
|
C’est la perspective dont
l’exécution est la plus simple ; elle convient très bien aux dessins rapides , mais elle déforme sensiblement l’objet
représenté. Principe : Toutes les faces frontales
sont dessinées en vraie grandeur. Toutes les arêtes non
frontales se dessinent suivant des « fuyantes »
inclinées d’un même angle µ (lire :
angle alpha) et sont réduites dans un rapport appelé : |
|
La
perspective cavalière d'une figure est
caractérisée par l'angle µ ( alpha) et le coefficient
"k" .
- Le parallélisme est conservé : les arêtes parallèles sont représentées par des segments parallèles .
-
les
fuyantes , ou lignes de fuite , parallèles entre elles
font un angle µ
avec l'horizontale .
Par exemple
: sur les fuyantes , avec k = 0,6 , une arête de
longueur 5 cm est représentée par un segment de longueur : 3 cm ( 5 cm fois 0,6 )
|
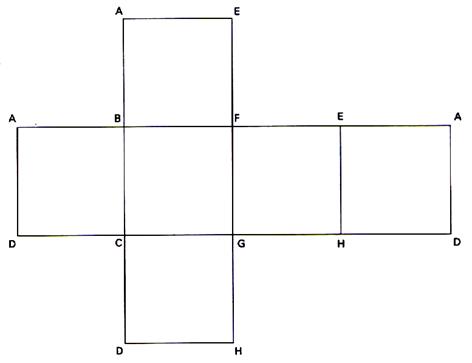
3°) développement du cube . |
Prenons le cube suivant ( les
sommets sont repérés par des lettres):
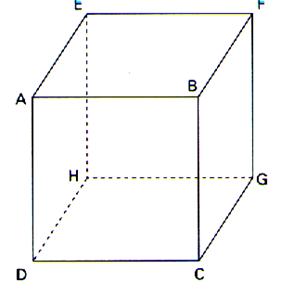
Ci dessous on obtient le "développement" du
cube ci- dessus . la figure obtenue est aussi
appelée : patron.
|
2 bases et une surface latérale ( 4 carrées alignés)
|
Pour se souvenir :
Si le cube est une pièce d'habitation .
La base 1 est la face supérieure c'est le plafond ; la base 2 est la face inférieure , c'est le sol de la pièce .
La surface latérale est le développement des murs
.
|
4° )
Aire et volume. |
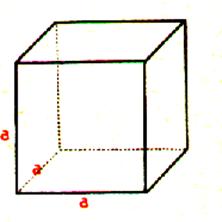
Les arêtes ont la même longueur
.
Si la
longueur de l'arête est notée
"a" .
Aire latérale ( 4 faces ) : A
= 4 a²
Aire totale ( 6 faces) :
A = 6 a²
Volume du cube :
V = a3
Application :
Un cube a une
arête de longueur "a
= 30 mm"
Calculer :l' aire latérale (
en mm² et cm² ) , l'aire totale ( cm²)
, le volume du cube ( mm3 puis cm3 ) .
Solution :
Aire latérale ( 4 faces ) :
A = 4 a² ;
A = 4 fois 30 fois 30 = 4 
30 30 = 3 600 mm² ; ou
36 cm²
Aire totale ( 6 faces) :
A = 6 a²
; A = 6 fois 3 fois 3 = 6 3 3 = 54 cm²
Volume du cube :
V = a3
; V = 303030 = 27 000 mm3 ou 27
cm3
|
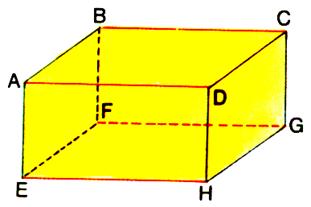
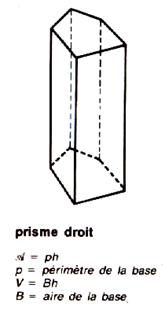
1°) description |
|
Il possède 6 faces : Les deux faces
horizontales sont les bases. Les quatre
autres faces sont dites « latérales »(l’ensembles
des quatre faces assemblées est appelé : surface prismatique ) Il
possède : 8
sommets : A ; B ;C ;D ;G ;H
; E ; F 12
arêtes : ce sont les bords des faces qui le limitent
,(on dit aussi
« intersection de deux plans » ) |
|
|
Les faces sont des rectangles .
|
Comme pour le cube , les arêtes aboutissant à un même sommet sont
perpendiculaires deux à deux , les faces opposées sont parallèles deux à
deux et les faces ayant
une arête commune sont perpendiculaires .
Chaque
face étant un rectangle , les arêtes opposées d'une
même face sont parallèles .
|
2°) représentation en perspective cavalière. |
( voir la perspective d'un cube)
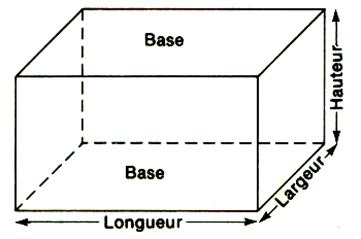
Pour effectuer la
perspective cavalière du parallélépipède rectangle il faut connaître comme dimensions : la longueur
, la hauteur , la largeur , ( ou
profondeur) , le coefficient "k" , et l'angle alpha . Procédure : tracer la face en
vraie grandeur , puis les fuyantes inclinées de alpha par rapport à l'
horizontal . Calculer la longueur des fuyantes ,
limiter la longueur des fuyantes , tracer les verticales .
Activité :
De la même façon que pour le
cube , représenter en perspective cavalière un parallélépipède rectangle de
longueur 7 cm , de largeur
5 cm et de hauteur 3 cm avec un angle "alpha" = 45 °
et "k" = 0 , 6
|
3° )
développement |
L’enveloppe du parallélépipède peut se « déplier » sur un plan .
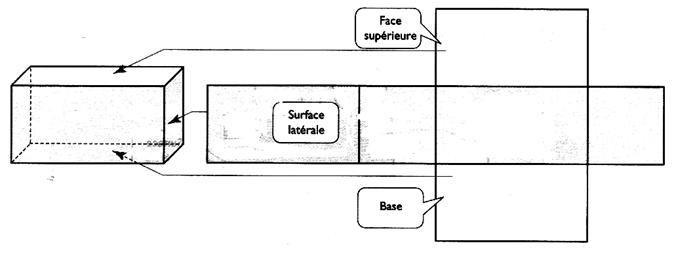
La figure obtenue s'appelle le "patron"
du parallélépipède.
|
4° )
Aire et volume. |
Si l'on
assimile le parallélépipède à la forme
d'une pièce d' habitation :
Une base est le plafond ; l'autre base est le sol ;
les parois verticales sont les côtés latéraux .
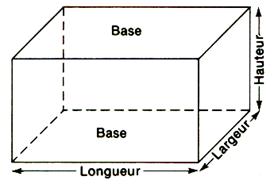
La longueur est notée :
L ; la
largeur : l : la hauteur : h .
Formules :
Aire latérale ( somme des aires des côtés latéraux ) :
A l = 2 h ( L + l )
Aire totale ( somme des aires
des côtés latéraux et des bases ) :
A t = 2 h ( L + l )
+ 2 L l
Volume du parallélépipède rectangle :
V = L l h
Remarque : pour les calculs les dimensions doivent être exprimées dans la
même unité de longueur .
Activités
« calculs »:
Un parallélépipède
rectangle a pour dimensions : L = 7,5 cm ; l = 50 mm ; h = 0,2 dm .
Calculer l'aire
latérale , l'aire totale ( exprimées en cm² et mm² ) et le volume ( exprimé en mm 3 et cm3 ).
Solution :
1°) on convertit dans la
même unité ( cm) les dimensions :
L = 7,5 cm = ; l = 50 mm = 5 cm ; h = 0,2 dm = 2 cm .
2°) Aire latérale ( somme des aires des côtés latéraux ) :
A l = 2 h
( L + l )
= 2 2 ( 7,5 + 5 ) = 50 cm²
; = 5000 mm²
3°) Aire totale ( somme des aires
des côtés latéraux et des bases ) :
A t
= 2 h ( L + l ) + 2 L l = 2 2 ( 7,5 + 5 ) + 2 7,5 5 ;
= 50 + 75 cm² = 125
cm²
4°) Volume du parallélépipède rectangle :
V =
L l
h =
7,5 5 2 = 75 cm3
|
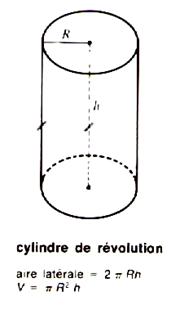
1° )
description |
Le cylindre est obtenu en
faisant tourner le rectangle OAA'O' autour de
l'axe ( OO')
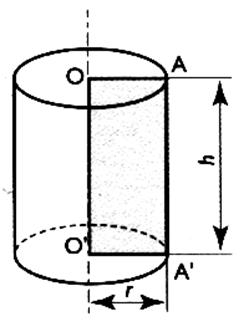
caractéristiques :
- le rayon est la largeur du
rectangle : r = lg [OA] = lg [O' A']
- la hauteur "h" est la longueur du segment A A' .
|
2°) représentation en perspective cavalière . |
Les bases du cylindre
sont des disques . En perspective ces
disques sont des "ellipses" . ( voir le tracé
des ellipses )
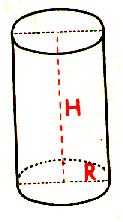
Ellipse : base
|
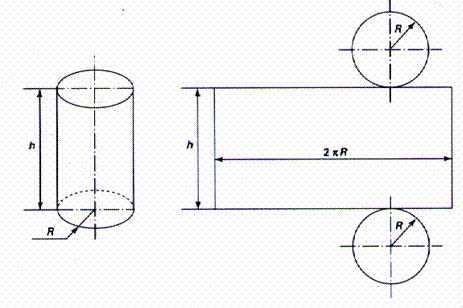
3° )
développement |
Le
développement du cylindre se compose d'un rectangle dont la longueur ;
L = 2p R et la largeur "l = h " et de deux
disques dont un porte le nom de
"base" , l'autre étant la face supérieure .
|
4°) Aire et volume. |
Voir le dessin ci dessus :
La hauteur étant notée :
"h" et le rayon : "R"
L'aire latérale : A l = 2p R h .
L'aire de la base ( et de la face supérieure ) : A b
= p R ²
L'aire totale ( l'aire latérale +
l'aire des deux disques) = 2p
R h +
(2p R ² )
Volume : V =
aire d'une base hauteur ; V =
p R ² h
Remarque
importante : ne pas oublier d' homogénéiser les
unités de longueurs!!
Application:
Un cylindre a pour dimensions : h = 110 mm et
R = 52 mm ; prendre
pi = 3,14
Calculer L'aire
latérale ( en
mm² et cm² ) ; L'aire de la base ( en mm² et cm² ); L'aire totale ( en mm² et
cm² ); le volume ( en mm3 et cm3 ).
Solution
:
a) L'aire latérale :
A l
= 2p R h . ; A l
= 2 3,14 52 110 =
35921,6 mm² ou 359 , 216 cm²
b) L'aire de la base ( et de la face supérieure ) :
A b = 2p R ² ; = 2 3,14 52 52 = 16981,12
mm² soit 169 ,8112 cm²
c) L'aire totale ( l'aire latérale +
l'aire des deux disques) :
A t = 2p R h + 2 (2p R ² )
= 35921,6 + 16981,12 =52902,72
mm² ou 529, 0272 cm²
d) Volume :
V = aire d'une base hauteur ;
V = 2p R ² h ; 2 3,14 52 52 110 = 1867923,2 mm3 ou 1867,9232 cm3
Corrigé
des activités :
1°) solutions :
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
, , |
dm3 |
, |
cm3 |
, |
mm3 |
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
7 |
6 |
5 |
7 |
9 |
8 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
7 |
8 |
5 |
0 |
7 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
5 |
4 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
8 |
3 |
2 |
|||||||
Solutions : on reprend le tableau rempli
dans l’activité 1
On
fait dans l’ordre : On complète de zéro ; on retire la virgule ; la
déplacer dans la colonne de droite de
l'unité demandée.
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
,, |
dm3 |
,, |
cm3 |
, |
mm3 |
|
||||||||||||||
|
|
|
|
|
|
|
0 |
0 |
1 |
7 |
6 |
5 |
7 |
9 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
5 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
7 |
8 |
5 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
2 |
8 |
5 |
4 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
8 |
3 |
2 |
|||||||
1
765 , 798 m3 = 1
765 798 dm3 ;
5,3
m3 = 53 000 dm3
78 507 dm3 = 78, 507 m 3
2854 cm3 = 0, 002 854 m3
5 832 mm3 = 5 , 832 cm3
|
|
|
|
|
|
Corrigé : Une cuve à fuel, en
tôle, a la forme d’un cylindre de révolution ayant 2 m de diamètre et 3,50 m de long. La surface latérale a
été mise en forme et soudée suivant l’une de ses génératrices. Les deux bases
sont assemblées à la surface latérale par soudure. Calculer : a) la longueur totale du cordon de soudure nécessaire à la
réalisation de la cuve. Périmètre de base circulaire : 3,14 fois 2 = 6,28 , soit 6,28 m ; la longueur totale du cordon de
soudure : ( 6,28 fois 2) + 3,5 = 16 ,06 , soit 16,06 m; b) L’aire de l’une des bases. 3,14 fois 1² = 3,14 fois 1 =
3,14 soit 3,14 m². c) L’aire latérale de la cuve. 6,28 fois 3,5 = 21,98 ,
soit 21,98 m² d) La surface de tôle nécessaire à la construction de la
cuve ; 21,98 + ( 3,14 fois 2) = 21,98 + 6,28 =
28,26 e) Le volume de la cuve en
m3 et la capacité en litres ;3,14
fois 3,5 = 10,99 soit 10,99 m3 ; capacité en litres :
10,99 m 3 , 10990 dm3 soit 10 990 litres. f)
La masse de fuel
contenue dans la cuve pleine ( masse volumique du
fuel : 850 kg/m3 ) : 10,99 fois 850 = 9 341,5 ,
soit 934,5 kg. On prendra : π
= 3,14 . On effectuera les calculs à 0,01 près par défaut. |
Masse volumique :
|
|
|
Une pyramide dont la base est un
triangle équilatéral de 15 cm de côté , a un
volume de 1 732 cm3 .
Calculer sa hauteur. Hauteur du triangle de base : h’ = 15 fois
(racine de 3) sur 2.= Aire de la base : B
= 15 fois 15 fois (racine de
3) sur 2. fois 1 demi.
Calcul de la hauteur de la
pyramide :
|
|
|
3 |
En prenant pour aire 50 cm² et pour épaisseur
3 mm, calculer la masse de la pièce ( masse
volumique du métal : 7600 kg/ m3 Volume de la pièce : V = 50 fois
0 ,3 soit 15 cm3 . La masse volumique du métal est de
7600 kg / mètre cube . ou 7,6 kg par décimètre
cube ; soit 7,6 g / c m3 :
masse de la pièce = 7,6 fois 15 = 114
soit 114 g ou 0,114 kg. |
|
