|
|
|
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : |
1°) Liste des cours sur les
calculs de volumes 2°) les solides de révolutions |
||||
|
|
|
|
|
||
|
|
|||||
|
|
|
|
|||
|
|
DOSSIER : Calculs aires et volumes du CYLINDRE
de révolution. |
|
|||
|
|
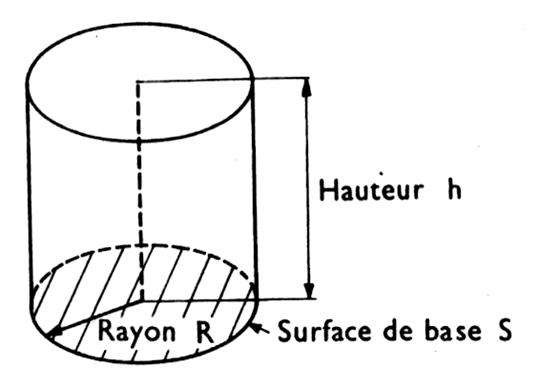
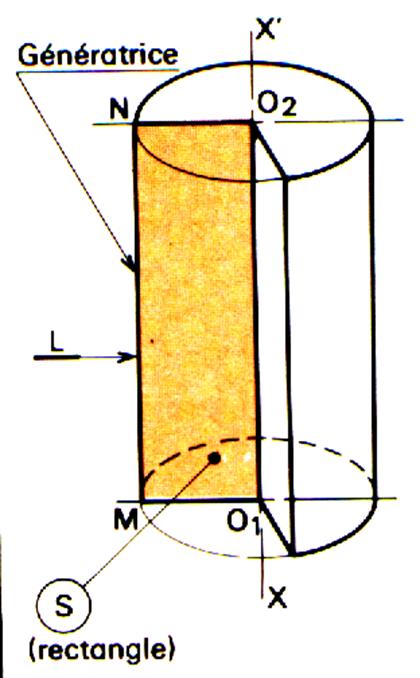
I
) Le cylindre de révolution : définition. |
|
|||
|
|
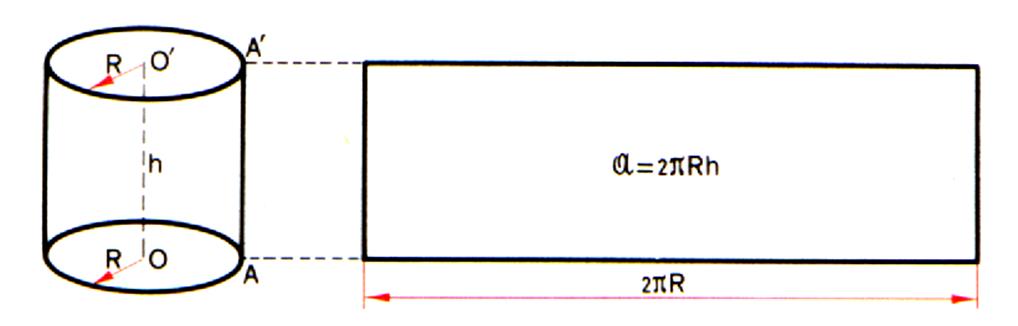
II ) Calcul de Aire
latérale d’un cylindre .
|
|
|||
|
|
III
) Calcul du
Volume d’un cylindre . |
|
|||
|
|
IV
) Activités
(exemples de calculs et exercices résolus ) |
|
|||
|
|
|
|
|||
|
|
V ) Situations
problèmes sur le cylindre……. |
|
|||
|
|
|
|
|||
Et Calculs
|
TEST |
COURS |
Interdisciplinarité |
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|||||||||
|
|
A retenir : |
|
|||||||||
|
|
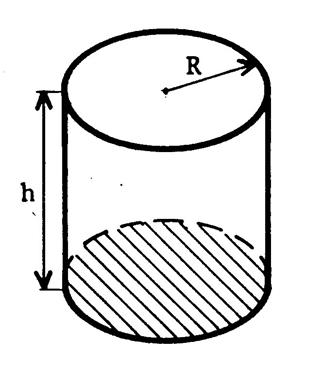
Le volume
« V » du prisme droit de hauteur « h » et dont l’aire de
la base est « B » |
|
|
|
|||||||
|
|
|
|
|||||||||
|
|
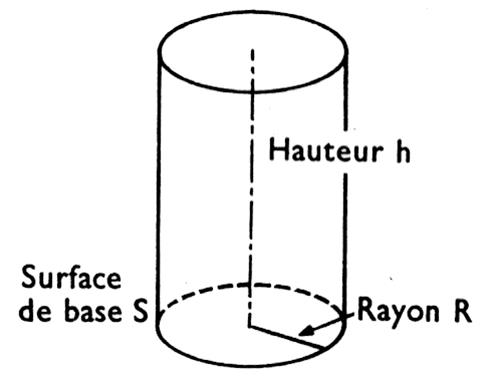
Appelons
« R » le rayon du disque de base. Vous savez que l’aire du disque est égale à « |
|
|||||||||
|
|
A retenir : |
|
|||||||||
|
|
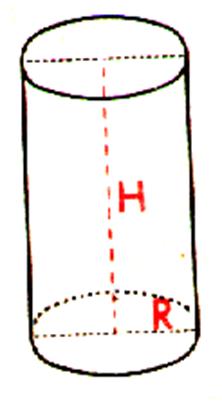
Le volume
« V » du cylindre de révolution de hauteur « h » et de
rayon « R » |
|
|
|
|||||||
|
|
|
|
|||||||||
|
|
Remarque : « V »
, « B » , « h » , « R » sont exprimés
avec des unités correspondantes. |
|
|||||||||
|
|
Remarque 1 : « V » ,
« B » , « R », et
« h » sont exprimés avec des unités correspondantes. -
Ce qui signifie que si
l’unité de « h » est le
« m » , « R » doit être en « m » , l’unité de
« B » sera le « m 2 » et l’unité de
« V » sera le « m 3 ». Ce qui signifie que si l’unité de « h »
est le «mm » ,
« R » doit être exprimé en « mm » , l’unité de
« B » sera le «mm 2 » et l’unité de « V »
sera le « mm 3 »…et ainsi de suite. |
|
|||||||||
|
|
|
|
|||||||||
|
|
Activité N°….. Complétez le tableau relatifs à des cylindres ( prendre |
|
|||||||||
|
|
|
|
|||||||||
|
|
|
Rayon |
Aire de la base |
Hauteur |
Volume |
|
|
||||
|
|
5 cm |
……78,5…cm² |
0,6 m =60 cm |
…4710…..cm3 |
|
||||||
|
|
……2…mm |
……12,56….mm² |
3,5 cm = 35 mm |
439,6 mm3 |
|
||||||
|
|
0,7 dm |
……153,86….cm² |
0,5 cm = 5….mm |
76,93 cm3 |
|
||||||
|
|
|
|
|||||||||
|
|
Activité N° ….. |
|
|||||||||
|
|
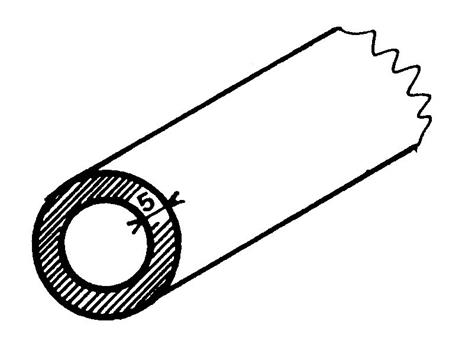
Ci –contre , un
tuyau de plomb à « 4 cm » de diamètre extérieur. Il a une épaisseur de « 5 mm » et une
longueur de 3 m. Calculez son volume et sa masse sachant que la
masse volumique du plomb est de « 11,3 g / cm3 ». |
|
|
||||||||
|
|
Le volume « V » se calcule grâce à la
formule « V = B x h » ·
La base est une
couronne de rayon extérieur : R =
40 mm / 2 =
20 mm et le rayon
intérieur « r » : « 20 – 5 = 15 mm ». ·
Aire de la base ( en mm²) :
B = ( 3,14 x 20
x 20 )
- ( 3,14 x 15
x 15 )
; B = 1256
- 706,5 ; B = 549,5 mm² ·
Volume du tuyau (mm3 ) : ( V) V = 549,5 x
3 000 = 1 648 500 mm3 ; V =
1648,500 cm3 ·
Masse du tuyau en
« g ». 1 648,
500 x 11,3 =
18628,05 ; masse du tuyau = 18,62805 kg |
|
|||||||||
|
|
|
|
|||||||||
|
|
Activité N°….. |
|
|||||||||
|
|
|
|
|||||||||
|
|
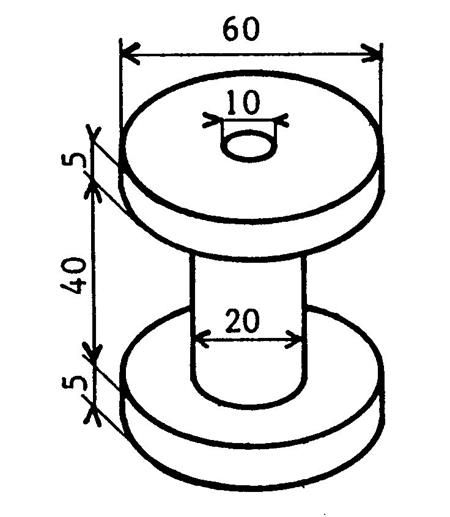
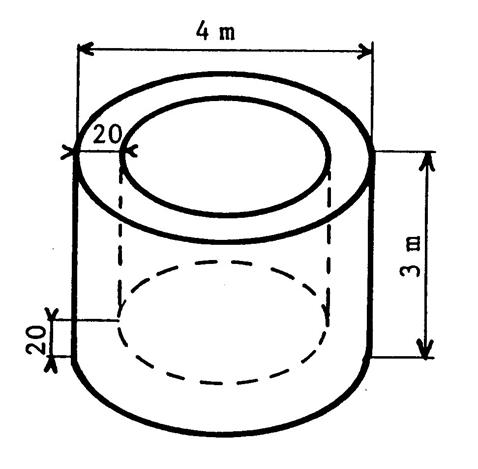
Le dessin ci-contre représente une bobine (de cable électrique ). Elle est constituée par « 3 » cylindres
superposés traversés par un « cylindre » creux . Les dimensions sont en « cm ». On vous demande de calculer le volume de cette
bobine ( : quantité de matière qui constitue cette bobine
). Volume du cylindre du dessus en « cm 3 ». 3,14 x …30 ..² x …5 ….= …14 130…. Volume du cylindre central en « cm3 » : 3,14 x …10 .² x …40 …..= …12 560…….. Volume du cylindre creux : 3,14 x …5…²
x …50….= …3 925…. |
|
|
||||||||
|
|
Volume de la bobine en « c m 3 » . (2
x ……14 130……… + ………12 560…….) - ……3 925……….= ………36 895 cm 3……….. |
|
|||||||||
|
|
|
|
|
|
|
V ) Situations
problèmes sur le cylindre……. |
|
|
|
|
|
|
|
|
|
Problème 1 : Une ligne électrique de 30 km de long est constituée par 3 fils de
cuivre de 1cm de diamètre. Quelle est la masse de ces fils sachant que la
masse volumique du cuivre est de
« 9 kg / dm3 » |
|
|
|
|
|
|
|
|
|
Problème 2 : Un bassin en ciment à la forme de la figure
ci-contre. L’épaisseur des parois et du fond est de 20 cm. Calculez le volume de la maçonnerie ? (Cela revient à
rechercher la quantité de matière ciment plus sable ..) |
|
|
|
|
|
|
|
|
|
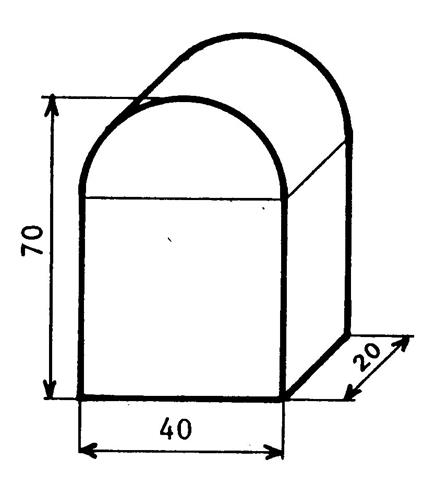
Problème 3 : Une borne est constituée par un parallélépipède
rectangle surmonté d’un demi-cylindre. Les dimensions de la figure ci-contre sont en « cm ». Calculez le volume de la borne.. |
|
|
|
|
|
|
|
|
|
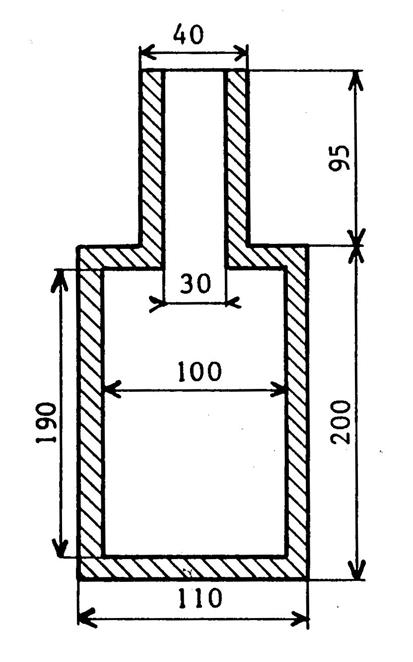
Problème 4 : Le dessin ci-contre représente un flacon
cylindrique en verre vu en coupe .. Les dimensions sont en « mm ».. L’épaisseur du verre est de « 5 mm ». Calculez le volume en verre utilisé pour faire ce
flacon. |
|
|
|
|
|
|
|
|
|
Problème 5 : Un lingot de cuivre pèse « 84,78 kg » . 1°)Sachant que la masse
volumique du cuivre est d’environ « 9 kg / dm3» quel est
le volume de ce lingot ? 2°) Le cuivre étant très ductile
, avec ce lingot, on veut fabriquer un fil cylindrique de « 1
mm » de diamètre. Quelle longueur de fil obtiendra-t-on ( en km) ? ( prendre pi =
3,14 ) |
|
|
|
|
|
|
|
|
|
Travaux auto_ formatifs |
|
|
|
|
|
|
|
CONTROLE : 1°) Qu’est ce qu’un un
cylindre de révolution. 2°) Donner ses
caractéristiques principales . 1°)Représenter en perspective un cylindre de révolution. Construire un
cylindre avec un feuille de papier
|
|
|
|
|
|