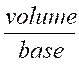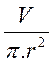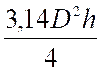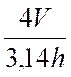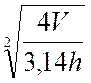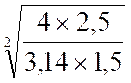Travaux  niveau   VI Pré requis     :Dos 124 et 125   et  Dos 130 et 131  

Les conversions des unités de  volume

Disques

Index        

Objectif précédent :

Le cylindre 

Objectif suivant :

1°) liste des cours sur   les volumes 

2°) les solides de révolutions

2°) les solides de révolutions

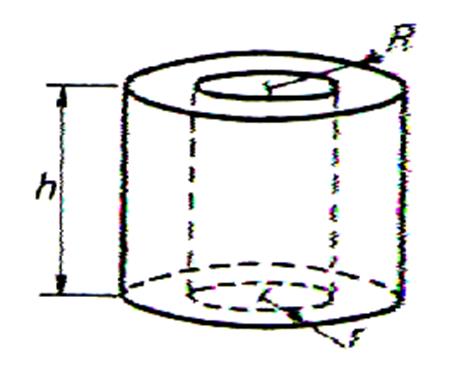
Calculs sur le cylindre ; le  CYLINDRE CREUX ou MANCHON CYLINDRIQUE.

I )  Rappel : Surface latérale d’un cylindre droit

II )  Surface totale du cylindre .

III ) Rappel : calcul du  VOLUME DU CYLINDRE

IV )CYLINDRE CREUX ou MANCHON CYLINDRIQUE

Application , calculs  types ; . ;;

Epreuve :  CONTROLE CONTINU :

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

Travaux niv V.

Dos 179

Interdisciplinarité  niv V

Dos 188

Dos 219

COURS

I ) Rappel :   Surface latérale d’un cylindre droit

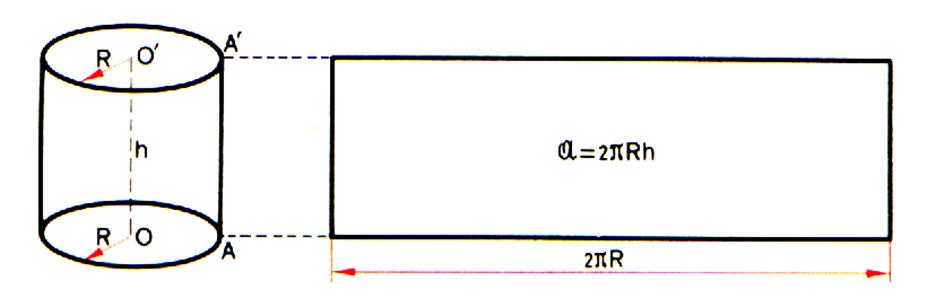
La surface latérale d’un cylindre droit est égale au produit de la longueur de la circonférence de sa base par sa hauteur :

1^ère traduction :

Surface latérale = Circonférence de la base x hauteur

2^ième traduction :

A = 2pr  x   h

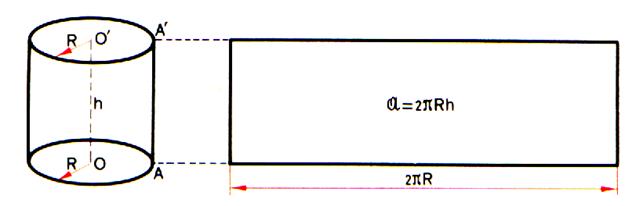
Aire latérale d’un cylindre : En coupant un cylindre de révolution suivant une génératrice (AA’), on peut appliquer sa surface latérale sur un plan.

Si on développe la surface latérale  ‘ a )  on obtient un rectangle dont la largeur est égale à la hauteur  du cylindre et dont la longueur est égale à la longueur du cercle de base.

Application :  Calculer  la surface latérale d’un cylindre de révolution. ( rayon = 10m ; hauteur = 30m , pi = 3,1416 )

A = 2pr h

A = 23,1416 10m30m                      ; ( remarque :   m  x   m = m² )

II )  Surface totale du cylindre :

La surface totale est la somme de la surface latérale ( Al)   et de la surface des deux bases  ( 2 B) .

Soit :    A totale = A latérale  + 2 B =    2 p r x  h +  2 p r²   =   2 p r ( h + r )

Application :

 Calculer  la surface totale d’un cylindre de révolution. .( rayon = 10m ; hauteur = 30m , pi = 3,1416 )

A totale = A latérale  + 2 B = 2pr h +2pr² = 2pr  ( h+r)

A totale = 23,1416 10 m (30m + 10m ) ; remarque 30m + 10m = 40m

III ) Rappel : calcul du  VOLUME DU CYLINDRE.

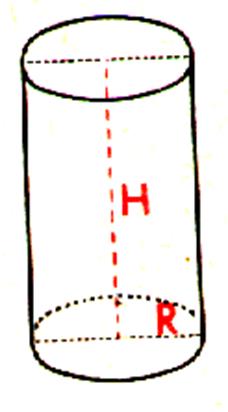
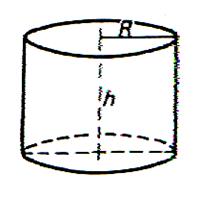
Le volume ( V ) d’un cylindre est égal au produit de l’aire de la base ( disque) multipliée par la hauteur. (précaution importante :prendre les mêmes unités de longueur)

Formule :

V = pR² H

Application : Trouver le volume d’un cylindre de 0,40 m de rayon et de 2 m de hauteur.

Volume :         V = p R² h    = 0,4m 0,4m3,1416 2  = 1,005312 m²

HAUTEUR :  On obtient la hauteur d’un cylindre en divisant le volume par la surface de base .

h =   =

IV )CYLINDRE CREUX ou MANCHON CYLINDRIQUE

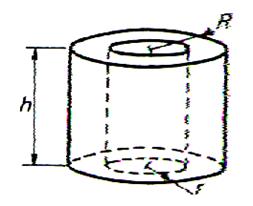
Définition : On appelle manchon cylindrique  le volume  compris entre les parois latérales de deux cylindres concentriques de même hauteur.

La base du manchon cylindrique est une couronne    ( Info Plus ++++)

Le volume du manchon cylindrique est égal au produit de la surface de sa base  (couronne) par sa hauteur.

V = p (R² – r² ) h

Application :

Calculer  le volume  d’un manchon ou cylindre creux . .( Rayon  = 10 m ;rayon = 8m  ; hauteur = 30m  , pi = 3,1416 )

Réponse :

V = p (RR – rr ) h 

V = 3,1416  (1010 – 88 ) 30

V =  3,1416  (100 m²– 64m² ) 30m

V = 3392,928 m³

Autres calculs :

Quel diamètre convient-il  de donner à un cylindre de 1,50 m de haut pour obtenir une capacité de 25 hectolitres ?

a)    il faut  convertir l'unité de capacité en unité de volume métrique .

( à savoir :        1 hl = 100 litres ;                            1 litre = 1 dm ³ ;                       1000 litres = 1000 dm³  = 1 m³  )

B )   On sait que le volume d'un cylindre se calcule  avec la formule : V =  ; on cherche "D"

Procédure :  sur les transformations successives.

Activités  1:

Un cylindre a pour  dimensions : h = 110 mm  et     R =  52 mm  ; prendre pi = 3,14

Calculer L'aire latérale  ( en mm² et cm² ) ; L'aire de la base ( en mm² et cm² ); L'aire totale ( en mm² et cm² ); le volume ( en mm³ et cm³ ).

Solution :

a) L'aire latérale :

  A _l = 2p R h .  ; A _l = 2 3,14  52  110   =   35921,6 mm² ou   359 , 216 cm²

b) L'aire de la base ( et de la face supérieure ) :

 A  _b = 2p R ²  ; = 2 3,14  52  52  = 16981,12  mm² soit   169 ,8112 cm²

          Exemple de situation problème :  On construit un réservoir cylindrique pour une commune de 1 800 habitants. On estime à 35 L d’eau par jour la consommation de chaque habitant. a) Quel doit être le volume du réservoir pour que la réserve d’eau soit assurée pour 3 jours? b) Le réservoir ayant 6 m de diamètre, quelle sera alors, à 1 cm près, la hauteur de l’eau?

1.     Consommation pour un jour :  1800 fois 35 L=63 000 L ;

2.     Consommation pour 3 jours : 63 000 fois 3 = 189 000 L

3.     Volume d’eau :  189 000 L = 189 000 dm³ = 189 m³

4.     Surface de base du réservoir :  3,14 fois 3 fois 3 = 28,26 m².

5.     Hauteur de l’eau dans le réservoir : 189 m³/ 28,26 m² = 6,6878  soit au cm prés : 6,69 m

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1°)Donner la formule permettant de calculer  la surface latérale d’un cylindre de révolution.

2°)Donner la formule permettant de calculer  la surface totale d’un cylindre de révolution.

3° ) Donner la formule permettant de calculer  le volume  d’un cylindre de révolution.

4° ) Donner la formule permettant de calculer  le volume  d’un manchon ou cylindre creux .

5°)

6°)

EVALUATION

Pour les calculs suivants on considérera que les longueurs sont exprimées dans la même unité : le centimètre « cm »

1°) Calculer  la surface latérale d’un cylindre de révolution.( rayon = 10 ; hauteur = 30 , pi = 3,1416 )

2°) Calculer  la surface totale d’un cylindre de révolution. .( rayon = 10 ; hauteur = 30 , pi = 3,1416 )

3° ) Calculer  le volume  d’un cylindre de révolution. .( rayon = 10 ; hauteur = 30 , pi = 3,1416 )

4° ) Calculer  le volume  d’un manchon ou cylindre creux . .( Rayon  = 10 ;rayon = 8 ; hauteur = 30 , pi = 3,1416 )

INTERDISCIPLINARITE

1°) On fait creuser un puits de 12 m de profondeur sur 1,50 de diamètre.

Quel est le volume de terre extrait ?

2° ) Dans un vase plein d’eau , on plonge un lingot d’or de forme irrégulière. Sachant  que l’eau sortie remplit exactement un verre cylindrique de 4émm de diamètre et de 8 cm de hauteur, trouver le volume du lingot ( prendre pi = 22/7)

3°) On veut creuser un bassin circulaire de 0,60 m de profondeur qui contienne 215 hl d’eau . Quel est le rayon de ce bassin ?

4°)On creuse un puits cylindrique de 8 m de profondeur et de 2,40 m de diamètre. Quel est le volume de terre enlevée ? La terre remuée augmente son volume de 1/5 . Combien faudra-t-il de tombereaux de 2 m³  pour évacuer la terre provenant du puits ? On l’épand sur un jardin de 25 a ; quelle sera l’épaisseur moyenne de la couche ainsi obtenue ?

5°) On creuse un puits cylindrique de 8,50 m de profondeur. La maçonnerie des parois à 28 cm d’épaisseur et le diamètre intérieur  du puits et de 1,22 m.

A combien revient ce puits si les travaux de terrassement et d’enlèvement de la terre reviennent à 56,4 € par mètre cube et si le mètre cube de maçonnerie revient à  450 € ?

Epreuve :  CONTROLE CONTINU :

1°)

2°)

3°)

4°)