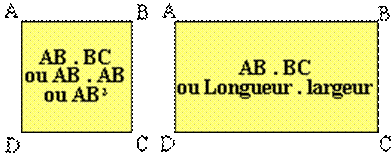|
WARMATHS |
Les formules |
|
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
Les Périmètres
Définitions:
Un périmètre mesure le contour d'une figure.
L'unité de mesure est
le mètre (m).
Les polygones:
Les triangles, les rectangles, les parallélogrammes sont des polygones.
Le périmètre d'un polygone
est égal à la somme des longueurs de ses côtés.
Remarques:
Pour un triangle
équilatéral il est plus simple de calculer: P=3.c
où c est la longueur d'un côté.
Pour un parallélogramme (ainsi que le cas particulier du rectangle) vous
utiliserez la formule: P=(L+l).2
où L est la longueur, l est la largeur. Notez que L+l est appelé demi-périmètre.
Pour un losange (donc pour un carré aussi) la formule est: P=4.c où c
est la longueur d'un côté.
Les cercles:
La formule est: P=2.pi.R où pi vaut environ 3,14 et R est la mesure d'un rayon.
Les Aires
Définitions:
Une aire mesure une surface.
L'unité de mesure des
aires est le mètre carré (m2).
Les triangles:
|
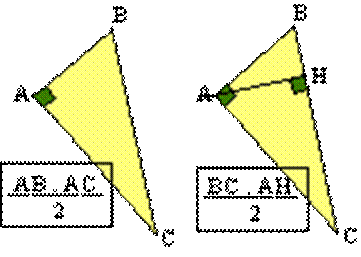
Quelconques: Dans la formule le côté [BC] est considéré comme la base. La droite
perpendiculaire à cette base et passant par le sommet opposé A est la hauteur relative à cette
base. Il y a trois côtés dans un triangle et donc trois bases possibles avec
leur hauteur relative. D'où trois formules. |
|
|
Triangle rectangle: Nous pouvons bien sûr utiliser l'une des formules du triangle quelconque,
à condition d'avoir les éléments nécessaires (longueurs de côté, de hauteur).
Il est souvent plus facile d'utiliser le fait que le triangle rectangle est la
moitié d'un rectangle. La formule utilise les longueurs des côtés de l'angle
droit.. |
|
Remarque:
Les aires des triangles isocèles
et équilatéraux se
calculent comme pour les triangles quelconques. Certains triangles isocèles
sont aussi rectangles...
Les
quadrilatères:
LES PARALLELOGRAMMES
|
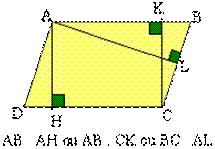
Il y a plusieurs façons de calculer l'aire d'un parallélogramme. Tout
dépend des dimensions connues. Il est nécessaire de connaître la longueur
d'un côté (pris comme base) et la hauteur qui lui est relative. Par exemple: si AB est connu il
faut connaître la hauteur qui passe par A (comme [AH]) ou par B, par C ou par
D ou encore par n'importe quel point du côté (DC) ou (AB). Toutes ces
hauteurs sont égales. La formule générale est: Base*Hauteur |
|
|
Le calcul de l'aire d'un parallélogramme est déduit de celui de l'aire
d'un rectangle. Sur la figure ci-contre: les triangles AHD et BKC sont superposables
de même aire. Calculer l'aire de ABCD revient à calculer l'aire du rectangle
ABKH: AB*AH. |
|
|
Cas particuliers: les rectangles.
|
|
|
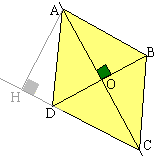
Cas particulier: le losange. Si nous connaissons la longueur de ses diagonales, nous pouvons
découper un losange en quatre triangles rectangles superposables (dans un
losange, les diagonales se coupent perpendiculairement en leur milieu). Sur la figure ci-contre: l'aire du losange ABCD est égale à quatre
fois l'aire de AOB. Soit: 4*(OA*OB)/2 ou 2(OA*OB) ou encore: AC*OB (car 2OA=AC). Bien entendu, rien ne vous empêche d'utiliser la formule générale des
parallélogrammes si vous en connaissez les éléments (une base et sa hauteur
relative) |
|
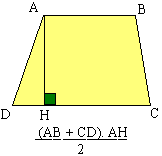
LE TRAPEZE.
|
Quelque soit le type de trapèze (quelconque, isocèle ou rectangle) la formule
à utiliser est toujours la même. [AB] et [DC] sont appelées petite base (b)
et grande base (B). [AH] est une
hauteur (h). La formule est: (B+b)*h/2 La distance entre les deux bases (hauteur du trapèze) n'est pas
forcément toujours donnée par la mesure du seul [AH] comme pour toute distance entre deux droites
parallèles. |
|
|
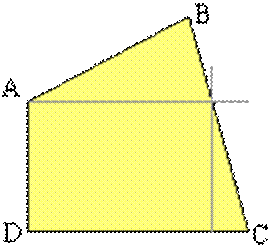
Dans ce cas il est nécessaire de découper la surface en surfaces de
base. Sur l'exemple ci-contre deux droites parallèles à deux côtés du quadrilatère
(la première à être tracée est celle qui passe par A) permettent de partager
le quadrilatère en un rectangle, un triangle rectangle et un triangle
quelconque. Une autre façon serait de tracer une droite parallèle à (AD) et
passant par B. Pour les calculs il est évidemment nécessaire de connaître certains
éléments généralement donnés par le contexte du problème. |
|
Les polygones:
Les polygones sont des
figures planes ayant plus de deux côtés (les triangles et les quadrilatères
sont des polygones). Nous donnons ici un exemple de polygone à 5 côtés. Pour en
calculer l'aire il est nécessaire de partager sa surface en polygones dont nous
connaissons une formule (tels que: triangles, quadrilatères).

Pour enduire d'un produit bleu le mur de cette mansarde il est d'abord
nécessaire d'en connaître l'aire afin de calculer la quantité de produit à
acheter. Nous avons les dimensions en mètres et nous savons que les angles en A
et B sont droits.
Nous pouvons décomposer la surface de différentes manières (tracés en
gris):
1° En un rectangle ABFE, un triangle rectangle EID et un trapèze
rectangle CDIF.
2° En un rectangle EIHA, un trapèze rectangle BCDH et un triangle
rectangle EID.
3° En deux rectangles EIHA et IFBH, un triangle rectangle EID et un
trapèze rectangle CDIF.
4° En un trapèze rectangle AHDE, un rectangle BFIH et un trapèze
rectangle CDIF.
5° En deux trapèzes rectangles AHDE et BCDH.
Avec les données du problème nous pouvons utiliser n'importe quelle
manière, la plus simple étant préférable! Les dimensions manquantes sont
calculées par soustraction. Par exemple pour calculer l'aire du triangle
rectangle EID: EI=3,1m et ID=HD-HI soit
ID=4,3-1,7=2,6m. Et aire EID=(IE*ID):2. Nous trouvons
4,03m2.
En utilisant la cinquième manière nous trouvons:
Aire
AHDE=(AE+HD)*AH/2 soit 9,3 m2
Aire
BCDH=(CB+DH)*HB/2 soit 9,125 m2
Aire
du mur à enduire=9,3+9,125=18,425 m2
Un conseil: si vous n'êtes pas à l'aise avec ces calculs d'aires, entraînez
vous en effectuant les calculs avec les autres manières. Vous devez trouver
exactement la même aire bien sûr.
Disques et secteurs:
L'aire d'un disque est donnée par la formule pi*R2
où pi est souvent pris égal à 3,14 (pour plus de précision voir la touche
correspondante de votre calculatrice) et R est la mesure du rayon du disque.
Un secteur de disque est déterminé par un angle au centre (le sommet de
l'angle est au centre du disque). Un demi-disque, un
quart de disque sont des cas particuliers de secteurs de disque. Leur aire est
respectivement pi*R2 /2 et
pi*R2 /4. Voici un
exemple de calcul de l'aire d'un secteur de disque dont l'angle au centre
mesure 110° et le rayon 3cm:
|
L'aire du secteur est proportionnelle
à la mesure de l'angle au centre. Pour le disque complet l'aire est pi*R2
et correspond à un angle au centre de 360°. Si s est l'aire du secteur
correspondant à l'angle au centre de mesure 110° alors les produits en croix
permettent d'écrire: pi*R2*110=360*s et s= (pi*R2*110)/360 Si le rayon R mesure 3cm alors s=8,64cm2 environ (à 1/100
de cm2 près ou 1mm2 près) |
|
Si au lieu de 110° nous avons un angle de mesure quelconque a alors la formule de l'aire du secteur
circulaire d'angle au centre a et de
rayon R est:(pi*R2*a)/360.
Aires latérales et volumes de
solides:
Définition:
L'aire latérale d'un solide est la somme des aires des faces qui ne sont
pas les bases.
L'aire totale des faces d'un solide est la somme de l'aire latérale et
des aires des bases. Si il n'y a pas de base (cas de la sphère) l'aire latérale
est l'aire totale.
L'unité de mesure d'un volume
est le mètre cube (m3)
Définitions: Un prisme droit est un solide qui possède deux bases
parallèles (contenues dans deux plans parallèles sur la figure ci-dessous) et
dont les faces latérales sont des rectangles.
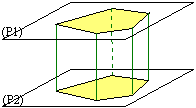
Le prisme est droit lorsque ses arêtes latérales (en vert sur le dessin)
sont perpendiculaires aux deux bases.
La hauteur d'un prisme est la distance entre les deux plans de base.
Pour un prisme droit la hauteur est égale à la longueur d'une arête latérale.
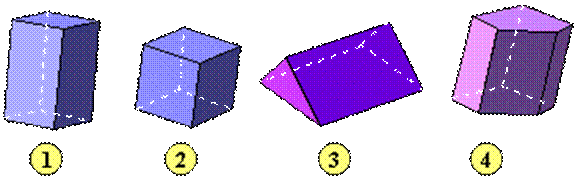
Exemples:
|
Fig
1: le parallélépipède
rectangle (ou pavé droit) Fig
2: le cube |
Fig
3: prisme droit à base triangulaire. Fig
4: prisme droit à base quelconque. |
Calcul de l'aire latérale:
Il suffit d'ajouter toutes les aires des faces latérales. Ces aires se
calculent à l'aide de la formule de l'aire du rectangle.
Pour le cube il s'agit d'aires de carrés.
Pour le pavé droit, les faces latérales sont de même aire deux à deux.
Calcul du volume
Quelque soit le prisme son volume se calcule avec la formule: V=B.h où « B » est l'aire de la base (qui est calculée à l'aire des
formules sur les polygones comme le triangle, le rectangle,..), « h » est la hauteur du prisme.
Pour le cube, la formule devient: V=c3 où c est la longueur d'une arête.
Pour le pavé droit, la formule s'écrit: V=L.l.h où L
est la longueur, l est la largeur et h est la hauteur du pavé droit.
|
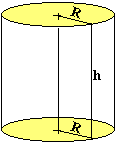
Les bases sont des disques de même rayon R. La face latérale se "déroule" en formant un rectangle dont
la largeur est la hauteur h du
cylindre et la longueur le périmètre de l'un des disques 2.pi.R. L'aire de
cette face latérale est donc: A=2pi .R.h d'après la formule utilisée pour l'aire d'un rectangle. Le volume se calcule avec la formule: V=pi.R2.h Remarque: pi.R2 est l'aire de la
base, donc la formule du volume d'un cylindre peut s'écrire comme la formule
du volume d'un prisme: V=B.h |
|
D'autres solides:
|
|
||
|
Les pyramides: les
faces latérales sont des triangles. L'aire latérale se calcule en ajoutant
les aires de ces triangles. Le volume d'une pyramide est calculé avec: V= où B est l'aire de la base
(triangle, rectangle,..) et h la
hauteur de la pyramide. |
Les sphères: l'aire
de la sphère est donnée par la formule: 4*pi*R2 où R est le rayon de la sphère. Pour le volume d'une boule, utilisez: V= |
Les cônes: l'aire
latérale d'un cône est donnée par la formule: pi*R*h ou R est le rayon du disque de base et h la longueur d'une
génératrice. La formule, pour le volume d'un cône est la même que la
formule pour le volume d'une pyramide, bien que le calcul de l'aire de la
base soit totalement différent: V= où B est l'aire de la base
(toujours un disque) et h la hauteur
du cône. |