WARMATHS

Pyramide

---

• Définitions.
• Pyramides quelconques.
• Pyramides régulières.
• Tétraèdre.
• Propriétés des pyramides régulières.
• Exemple.
• Tétraèdre régulier.
• Patrons:
• D'un tétraèdre.
• D'une pyramide régulière.
• Sections planes.
• D'une pyramide quelconque.
• D'une pyramide régulière.
• Formules.

---

Définitions:

Pyramides quelconques:

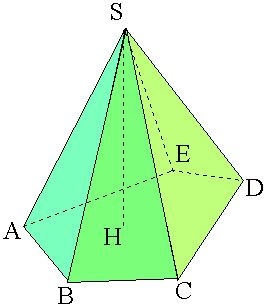
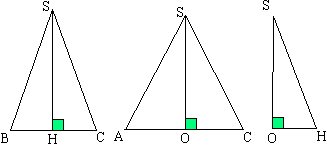
Nous obtenons une pyramide en joignant les sommets d'un polygone à un même point pris à l'extérieur du plan de ce polygone. La figure ci-contre a été obtenue en joignant les sommets A, B, C, D et E du polygone ABCDE au point S. S est appelé sommet de la pyramide. Les triangles SAB, SBC, SCD, SDE et SEA sont les faces latérales de la pyramide. Les segments [SA], [SB], [SC], [SD] et [SE] sont les arêtes latérales de la pyramide. Le polyèdre ABCDE est la base de la pyramide. Le segment [SH] tel que (SH) soit perpendiculaire au plan de la base, est appelé hauteur de la pyramide (le mot "hauteur" désigne aussi la longueur SH de ce segment).

Pyramides régulières: voir aussi le paragraphe qui traite de leurs propriétés.

Une pyramide est régulière lorsque les deux conditions suivantes sont vérifiées:

- sa base est un polygone régulier.

- sa hauteur passe par le centre de la base.

Exemples:

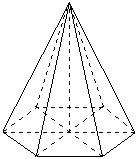
Pyramide régulière à base carrée, vue de différents points de vue:

Pyramide régulière à base hexagonale: Le centre de la base est défini par l'intersection des diagonales

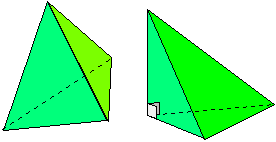
Tétraèdre:

Un tétraèdre est une pyramide à base triangulaire. Il possède six arêtes et quatre faces qui peuvent, chacune, faire office de base. Sur l'une des figures ci-contre nous avons représenté un tétraèdre dont deux faces sont des triangles rectangles. Il est possible que trois faces soient des triangles rectangles, mais pas les quatre faces.

Propriétés des pyramides régulières:

Soit une pyramide régulière de sommet S et de polygone de base ABCD.... Nous avons les propriétés suivantes:

- Les arêtes latérales [SA], [SB] , [SC] , [SD] ...ont la même longueur.

- Les faces latérales sont des triangles isocèles dont les côtés ainsi que les angles ont les mêmes mesures.

- La hauteur issue de S de l'un de ces triangles est appelée apothème de la pyramide régulière.

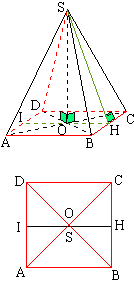
Exemple: pyramide régulière à base carrée

Comme ABCD est un carré alors le centre de la base est l'intersection des diagonales (ou des médianes comme [IH]). Le point H est le milieu de [BC]. L'apothème est [SH]. De nombreux calculs peuvent être effectués dans ce type de pyramide. Très souvent c'est le théorème de Pythagore qui est mis à contribution. Pour l'utiliser il faut découvrir le "bon" triangle rectangle (ce qui n'est pas toujours très visible sur la figure). Voici, sur les figures ci-dessous quelques uns d'entre eux:

Remarques sur ces triangles:

- SBC est isocèle. Ses côtés [SB] et [SC] ont pour longueur la longueur des arêtes de la pyramide. Le côté [BC] a pour longueur la longueur d'un côté de la base carrée. [SH] est l'apothème.

- SAC est isocèle. Ses côtés [SA] et [SC] ont pour longueur la longueur des arêtes de la pyramide. Le côté [AC] a pour longueur la longueur d'une diagonale du carré de base ( se calcule dans le triangle ABC rectangle en B: AC²=BA²+BC² ). [SO] est la hauteur de la pyramide.

- SOH est un triangle rectangle en O. [SH] est l'apothème. [OH] est une demi-médiane du carré de base (nous avons donc: OH= côté du carré/2). [SO] est la hauteur de la pyramide.

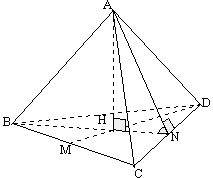
Cas particulier: le tétraèdre régulier.

Lorsque les six arêtes d'un tétraèdre ABCD sont de même longueur, les quatre faces du tétraèdre sont des triangles équilatéraux. Le tétraèdre peut donc être considéré de quatre façons, comme une pyramide régulière. Dans ce cas, nous avons un tétraèdre régulier.

Si A est considéré comme le sommet du tétraèdre régulier alors la face BCD est considérée comme sa base. La hauteur [AH] passe par l'intersection des médianes du triangle équilatéral de base (M et N sont des milieux d'arêtes).

Si vous connaissez la longueur d'une arête:

- Calculer l'apothème d'un tétraèdre régulier revient à calculer la longueur d'une médiane d'un triangle équilatéral (appliquer le théorème de Pythagore dans le triangle BNC rectangle en N par exemple: vous connaissez les longueurs de l'hypoténuse [BC] et d'un côté de l'angle droit [CN]: CN=CD/2).

- Calculer la hauteur AH d'un tétraèdre régulier est un peu plus long mais pas beaucoup plus compliqué:

- vous calculer l'apothème AN ( ou BN ou DM...) comme ci-dessus.

- vous calculez HN (Comme [BN] est une médiane alors H se trouve au tiers de la longueur de cette médiane à partir du milieu N). Nous avons: HN=BN/3 (ne pas oublier que BN=AN).

- vous appliquez le théorème de Pythagore dans le triangle AHN rectangle en H.

---

Patrons:

Un patron d'une pyramide est une figure dessinée sur un plan (celui de votre feuille par exemple). Après découpage, pliage et collage, la pyramide est ainsi vue en volumes.

Quelque soit la pyramide, il y a deux façons de dessiner son patron:

1. Dessiner d'abord le polygone de base, puis les triangles des faces latérales de façon que leur côté qui n'est pas une arête latérale soit un côté de cette base.

2. Dessiner les triangles des faces latérales de façon qu'ils aient tous un côté commun qui est une arête et le même sommet, celui de la pyramide. Le polygone de base est ensuite dessiné en s'appuyant sur le côté qui n'est pas une arête de l'un de ces triangles.

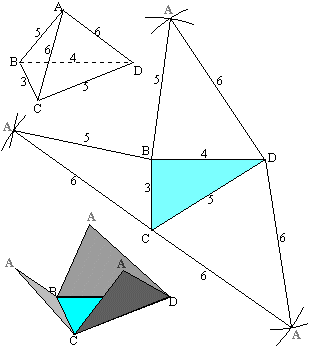
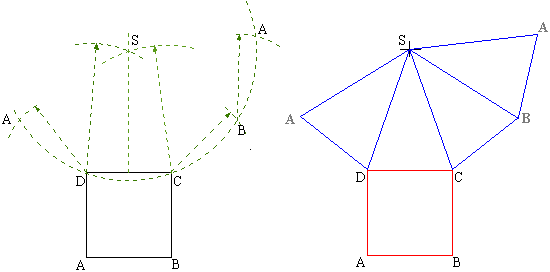
Exemple 1: patrons d'un tétraèdre en utilisant la première façon.

Le tétraèdre ABCD est donné avec toutes les longueurs de ses arêtes (ce qui simplifie le problème: bien souvent vous devrez les calculer). Il est d'abord représenté en perspective en prenant A comme sommet et BCD comme base; puis après un commencement de dépliage, afin de bien comprendre la méthode. Exécutez le patron en commençant par dessiner la base BCD (ce qui revient à dessiner un triangle connaissant les longueurs de ses trois côtés). Sur chacun des côtés de BCD construire les triangles représentant les faces latérales: ABD, ABC et ACD.

Remarque: BCD est un triangle rectangle (à démontrer en utilisant la réciproque du théorème de Pythagore).

Exemple 2: patrons d'une pyramide régulière à base carrée en utilisant la seconde façon.

La seconde façon est très conseillée pour dessiner les patrons des pyramides régulières du fait que leurs arêtes latérales ont la même longueur. Soit la pyramide SABCD où ABCD est un carré de côté 3cm de centre O et de hauteur SO=4cm (nous aurions pu vous donner l'apothème au lieu de la hauteur: les calculs se font alors dans le triangle SHB rectangle en H). Il nous faut tracer un arc de cercle de rayon SA (longueur d'une arête latérale). Comme SOB est rectangle en O alors SB^2=SO^2+OB^2 (1) (théorème de Pythagore). Nous connaissons SO. OB est la moitié de DB longueur d'une diagonale du carré ABCD. Comme ADB est rectangle en A alors DB^2=AD^2+AB^2. Donc : DB^2= 3^2+3^2et DB^2=18. La longueur d'une diagonale est donc environ 4,24cm (racine carrée de 18). De OB=DB/2 nous obtenons OB=2,12cm environ. En remplaçant dans la formule (1) SO et OB par leur valeur: SB^2=4^2+2,12^2 (environ) La longueur d'une arête est donc de 4,5cm environ.

Les traits en pointillés verts indiquent les constructions à effectuer. Vous remarquerez qu'ici encore le compas est très utilisé. Chronologie des constructions (ordre dans lequel vous devez les effectuer):

- Obtenir le centre de l'arc de cercle qui est le sommet de la pyramide: en pointant le compas (écartement égal à la longueur d'une arête, soit 4.5cm dans notre exemple) sur les extrémités d'un segment de 3cm de longueur ( ici le segment [DC] côté du carré de base) tracez deux arcs qui se coupent en S.

- Tracez l'arc de centre S et de rayon la longueur d'une arête (ici 4,5cm).

- Déterminer les sommets A et B du carré de base (nous avons déjà D et C): pointez le compas (écartement égal à la longueur d'un côté de la base) successivement en D, C et en B dès que celui ci est obtenu (le sommet A est déterminé deux fois sinon il manquerait la face SBA).

- Tracez le carré de base (à moins que vous ne l'ayez tracé dès le début).

Remarque:

L'aire latérale de cette pyramide est la somme des aires de quatre triangles isocèles de mêmes dimensions. L'aire de l'un de ces triangles (SAD par exemple) est (c.a)/2 où c= côté de la base et a l'apothème. Donc aire latérale= 4.(c.a)/2=(4.c.a)/2 où 4.c est le périmètre de la base carrée. Donc:

Aire latérale=(périmètre de base.apothème)/2

Cette formule est valide pour toutes les pyramides régulières (si la base est un polygone régulier de n côtés mesurant c, son aire latérale est n.(c.a)/2=(n.c.a)/2 où le périmètre de base est n.c).

Sections planes d'une pyramide:

La section plane d'une pyramide est obtenue en coupant la pyramide avec un plan. Nous ne rapellerons que l'étude des sections par un plan parallèle à la base de la pyramide.

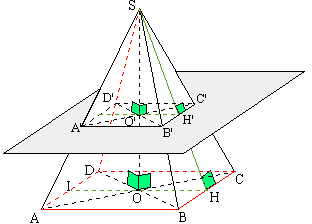
Avec une pyramide quelconque:

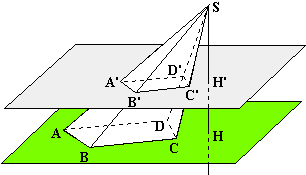
La pyramide SABCD est quelconque. Sa base ABCD est un quadrilatère quelconque. La hauteur d'une pyramide n'est pas toujours à l'intérieur de la pyramide. La pyramide ci-dessous en est un exemple. La droite (SH) est perpendiculaire au plan de base (en vert). Le plan de section (figuré en gris clair) est parallèle au plan de base. 

La face SAB est un triangle contenu dans le plan (SAB). Comme le plan (SAB) coupe les deux plans parallèles (plan de base et plan de section) alors ses intersections avec ces deux plans sont des droites parallèles: (A'B') est donc parallèle à (AB). De même pour (B'C') et (BC), (C'D') et (CD), (D'A') et (DA). La section plane de cette pyramide est donc un quadrilatère dont les côtés sont parallèles au quadrilatère de base. Comme (SH) est perpendiculaire au plan de base qui est parallèle au plan de section alors (SH) est perpendiculaire au plan de section en un point H'.

Remarques: Démontrez que (C'H') est perpendiculaire à (SH').

Traçons (CH) et (C'H'). C' est sur (SC) et H' est sur (SH). Les points S, C et H définissent un plan qui coupe les deux plans parallèles (de base et de section). Les droites (CH) et (C'H') sont donc parallèles.

Comme (SH) est perpendiculaire au plan de base alors toutes les droites de ce plan, passant par H sont perpendiculaires à (SH). Ce qui est le cas de (CH) qui est alors perpendiculaire à (SH).

Dans le triangle SCH, rectangle en H, la droite (C'H') est parallèle au côté (CH). Comme (CH) et (C'H') sont parallèles et (SH) est perpendiculaire à (CH) alors (SH) (ou (SH') ) est perpendiculaire à (C'H').

Avec une pyramide régulière:

Soit SABCD pyramide régulière à base carrée de sommet S. La section est un carré A'B'C'D' dont les côtés sont parallèles aux côtés correspondants du carré de base de la pyramide SABCD. La hauteur (SO) de la pyramide SABCD passe par le centre O' du carré A'B'C'D'. (SO) est perpendiculaire au plan de section. OO' est la distance du plan de section au plan de la base de la pyramide SABCD La pyramide SA'B'C'D' est aussi une pyramide régulière.

Comme les droites (O'B') et (OB) sont les intersections de deux plans parallèles (plan de base et plan de section) et du plan (SOB) alors ces deux droites sont parallèles (de même pour (OH) et (O'H') contenues dans le plan (SOH), (BC) et (B'C') contenues dans le plan (SBC), ...).

Formules:

Exemple: pyramide SABCD à base carrée ABCD de centre O, de côté 3cm et de hauteur SO=4cm. Soit le point H milieu de [AB]: SH est l'apothème de la pyramide.

Aire de la base: côté.côté=3.3=9cm².

Aire totale: aire latérale+aire de la base= (4.3.apothème)/2+9 (voir remarque sur exemple 2 du paragraphe précédent).

calcul de l'apothème: comme SOH est rectangle en O alors SH²=SO²+OH². La hauteur est SO=4cm

et OH=côté de la base/2=1,5cm

On obtient SH=4,27cm environ.

Aire totale=25,62+9 =34,62cm² environ.

Volume: (aire de base x hauteur )/3=(9 x 4 ) / 3=12cm³.