WARMATHS

Résumé : collège.

Les triangles

Définitions.
Propriétés.
Triangles particuliers.
Calcul des angles d'un triangle.
Calcul de côtés.
Constructions de triangles.
Propriété de Pythagore:

Théorème.
Réciproque.

Triangle obtenu avec un point d'un cercle et un de ses diamètres.
Droite des milieux.
Droite parallèle à un côté.

Définitions:

Un triangle est un polygone à trois sommets. Tout se compte par trois dans un triangle: 3 côtés, 3 angles, 3 médianes, 3 médiatrices, 3 bissectrices, 3 hauteurs, 3 façons de calculer son aire dont la formule est (base x hauteur) / 2.

Propriétés:

1. La somme des mesures des angles d'un triangle est égale à 180°.

2. La somme des mesures de deux côtés est supérieure (plus grande) à la mesure du troisième côté (inégalité triangulaire).

3. Droites particulières dans un triangle:

les médianes sont concourantes au centre de gravité.

les médiatrices sont concourantes au centre du cercle circonscrit.

les bissectrices sont concourantes au centre du cercle inscrit.

les hauteurs sont concourantes au point appelé orthocentre.

Triangles particuliers:

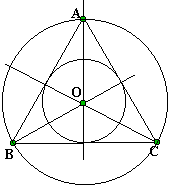
Un triangle équilatéral a ses trois côtés égaux, ainsi que ses trois angles (mesure égale à 180/3 = 60°). Ses médianes, médiatrices, bissectrices et hauteurs sont concourantes au même point. Les cercles inscrits et circonscrits sont donc concentriques (= même centre).

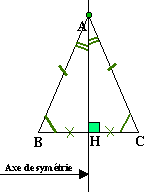
Un triangle isocèle a deux côtés égaux ainsi que deux angles. Le point commun à ces deux côtés est appelé sommet principal. La médiane, ainsi que la bissectrice et la hauteur qui passent par ce sommet sont aussi appelées principales. Ces droites sont confondues avec la médiatrice du côté opposé au sommet principal. Cette médiatrice est l'axe de symétrie du triangle isocèle.

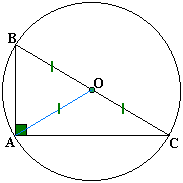
Un triangle rectangle possède un angle droit. Le côté opposé à l'angle droit est appelé hypoténuse, c'est toujours le côté le plus long du triangle rectangle. La somme des mesures des deux autres angles est 180 - 90 = 90°. Ces deux angles sont aigus et complémentaires. Les deux côtés de l'angle droit sont aussi deux hauteurs du triangle. C'est pourquoi l'aire d'un triangle rectangle est très facile à calculer ( = produit des mesures de ces deux côtés, divisé par 2).

Le centre du cercle circonscrit est le milieu de l'hypoténuse (ou: son diamètre est son hypoténuse). La longueur de la médiane relative (en bleu sur la figure) à l'hypoténuse est égale à la moitié de la longueur de l'hypoténuse.

Calcul des angles d'un triangle:

Pour calculer un angle d'un triangle, vous pouvez utiliser:

le cosinus de l'angle (après l'avoir éventuellement calculé). Nécessite l'utilisation d'une calculatrice.
La somme des angles d'un triangle est égale à 180°. Si vous en connaissez deux, vous pouvez calculer le troisième en soustrayant de 180° la somme des mesures des deux angles connus.
Les angles complémentaires (somme égale à 90°) ou supplémentaires (somme égale à 180°): si vous savez que deux angles sont complémentaires (respectivement: supplémentaires) et que vous connaissez la mesure x de l'un, vous pouvez en déduire en faisant 90-x (respectivement:180-x) la mesure de l'autre.
Les angles aigus d'un triangle rectangle sont complémentaires.
Les propriétés de certaines figures particulières: angles de 60° pour le triangle équilatéral, angles de 45° entre un côté du carré et l'une de ses diagonales, deux angles égaux dans le triangle isocèle (si la mesure x de l'angle principal est connu, vous calculez la mesure de chacun des angles égaux en faisant (180-x)/ 2 ).
une bissectrice: elle partage un angle dont on connait la mesure x en deux angles de même mesure x/2.

Attention: la mesure d'un angle obtenu à l'aide du rapporteur n'est pas démontrée. Vous pouvez cependant utiliser cette méthode pour vérifier vos calculs.

Calcul de côtés d'un triangle:

Pour calculer la longueur d'un côté d'un triangle, vous pouvez utiliser:

l'égalité: le côté dont vous cherchez la longueur est égal à un segment déjà connu (ou pour lequel vous pouvez démontrer l'égalité).
un triangle rectangle qui a pour côté le côté étudié. Ce qui permet l'utilisation du cosinus (si vous connaissez la mesure d'un des angles aigus du triangle rectangle) ou du théorème de Pythagore (voir plus loin dans cette page).
le théorème sur les droites parallèles coupant deux droites sécantes (voir plus loin dans cette page). Ce qui détermine des quotients égaux (a/b=c/d). Si vous connaissez a, b et c vous pouvez calculer d. Plus généralement: si vous connaissez trois termes de ces quotients, vous pouvez calculer le quatrième.
le segment des milieux ( voir plus loin da n s cette page). Si vous connaissez la longueur de ce segment, vous pouvez en déduire la longueur du côté qui lui est parallèle (en multipliant sa mesure par 2).

Constructions de triangles:

1. Triangles quelconques:

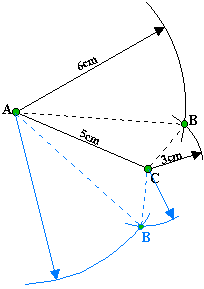
a. Nous connaissons les mesures des trois côtés: il faut que la propriété 2. de la section sur les propriétés soit vérifiée. Exemple: construire ABC tel que AB=6cm, BC=3cm et AC=5cm (vérifier que la somme des mesures de 2 côtés est supérieure à la mesure du troisième)

Nous pouvons commencer par tracer n'importe quel côté, puisqu'ils sont connus tous les trois. Commençons par [AC]: avec la règle et un double décimètre.

Pour trouver le troisième sommet B nous utilisons le compas. Tracez deux arcs de cercle: d'abord en pointant A avec un rayon de 6cm (AB=6cm) puis en pointant C avec un rayon de 3cm (CB=BC=3cm).

A l'intersection des deux arc se trouve le point B.

Il y a deux solutions (représentées, ci-contre, en noir puis en bleu). Vous n'en choisissez qu'une, bien sûr!

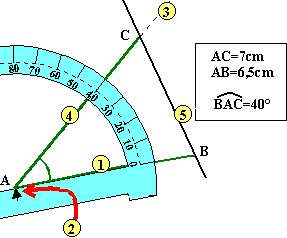
b. Nous connaissons les mesures de deux côtés et d'un angle: savoir utiliser un rapporteur est ici (comme dans le point suivant) bien utile. Exemple: construire ABC tel que AB=6,5cm, AC=7cm et l'angle en A mesure 40°.

Tracez le segment [AB] (de longueur 6,5cm).
Placez le centre du rapporteur en A et tournez le rapporteur de façon que son diamètre soit aligné avec (AB).
Tracez un petit trait en face de la graduation 40, enlevez le rapporteur et tracez une droite passant par A et le petit trait.
Portez sur cette droite 7cm à partir de A. Vous obtenez le sommet C.
Tracez la droite (BC) (ou le segment [BC] ).

Note: il existe une seconde solution de l'autre côté de (AB).

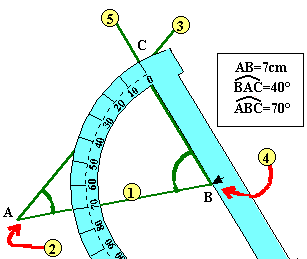
c. Nous connaissons les mesures d'un côté et de deux angles. Exemple: construire ABC tel que AB=7cm, l'angle en A mesure 40° et l'angle en B mesure 70°.

Tracez [AB] (de longueur 7cm).
Utilisez le rapporteur comme au b) ci-dessus.
Comme au b) ci-dessus.
Placez le centre du rapporteur en B. Tournez le rapporteur jusqu'à ce que la graduation 70 soit sur [AB] (le segment est parfois trop court; dans ce cas prolongez le avant de placer le rapporteur). Tracez un petit trait en face de la graduation 0.
Enlever le rapporteur et tracez la droite qui passe par B et le petit trait. Cette droite coupe la droite tracée au 3 en un point qui est le sommet C.

Note: une seconde solution existe....

2. Triangles particuliers (quelques exemples): Si nous savons que (le triangle à construire est ici appelé ABC):

a)Les trois côtés sont égaux: le triangle est équilatéral. Vous tracez le premier côté ([AB] par exemple) à la bonne longueur puis avec le compas dont la distance entre les pointes est égale à AB, pointe sèche en A, tracez un arc d'un côté de [AB]; pointe sèche en B, tracez un arc du même côté. Les deux arcs se coupent au troisième sommet du triangle à construire.

b)Les trois angles sont égaux: il nous faut tracer un triangle équilatéral mais il nous faut aussi la mesure d'un côté: si vous la connaissez, vous agissez comme en a) sans vous occuper des angles (de toute façon ils auront la même mesure: 60°). Sinon il vous faut d'abord la calculer...

c) Le triangle a deux côtés égaux de longueur connue et nous connaissons la mesure de l'angle principal (en A). Tracez le premier côté [AB] par exemple, A étant le sommet principal. Portez avec le rapporteur centré en A la mesure de l'angle et tracez le support du deuxième côté (demi droite d'origine A). Portez sur cette demi droite, à partir de A la mesure du côté [AC].

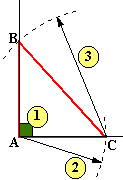
d) Le triangle est rectangle en A, que le côté [AC] mesure 6cm et que l'hypoténuse mesure 9cm. Dans ce cas l'hypoténuse est [BC]. Deux méthodes:

-Tracez l'angle droit d'abord (1)( avec l'équerre ou non, tout dépend de la précision que vous recherchez). Portez à partir de A, sur l'un des côtés de l'angle droit, le point C tel que AC=6cm (2). Avec le compas muni d'un rayon de 9cm, pointe sèche en C, tracez un arc de cercle qui coupe l'autre côté de l'angle droit au point B (3).

Remarque: la figure ci-contre est à l'échelle 1/2

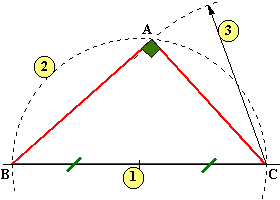
-Tracez l'hypoténuse [BC] d'abord. En déterminer son milieu (1). Tracer le cercle de diamètre l'hypoténuse (2). Avec la pointe sèche placée en C et un rayon de 6cm coupez le cercle en un point A (3)(il en existe deux symétrique par rapport à (BC), en choisir un). Tracer [AC] et [AB]. Le triangle obtenu ABC est rectangle en A et a les dimensions imposées.

Propriété de Pythagore:

Le théorème:

Si ABC est rectangle en A alors BC²=AB²+AC²

La propriété de Pythagore ne se rencontre que dans les triangles rectangles et seulement dans ces triangles. Si vous travaillez dans un triangle quelconque, vous ne pouvez pas l'utiliser directement: il vous faut décomposer ce triangle en triangles rectangles (en traçant une hauteur par exemple).

Cette propriété est très utile pour calculer la longueur d'un segment. Il faut que ce segment soit l'un des côtés d'un triangle rectangle (j'insiste..) et que vous connaissiez les longueurs des deux autres côtés.

Exemple:

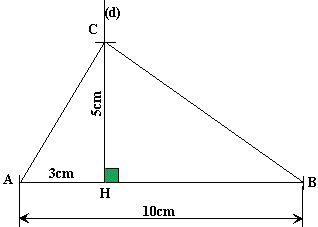
Soit le segment [AB] de longueur 10cm et le point H de ce segment situé à 3cm de A.

Tracer la droite (d) perpendiculaire en H à [AB] et placer sur (d) le point C tel que HA=5cm.

Calculer la longueur des côtés de ABC.

ABC est quelconque jusqu'à preuve du contraire.. Nous connaissons déjà la longueur du côté [AB] qui est 10cm.

Comme (d) est perpendiculaire à [AB] en H alors AHC (respectivement CHB) est rectangle en H.

Comme AHC (respectivement CHB) est rectangle en H alors AC²=HA²+HC² (respectivement : CB²=HC²+HB²).

Donc: AC²=3²+5² ; AC²=9+25 ; AC²=34 ; AC= 5,8cm environ (à 0,1cm près par défaut) (utilisation de la calculatrice avec la touche racine carrée: entrez 34 et appuyez sur la touche racine carrée). De même pour CB² mais il faut calculer d'abord la longueur de [HB]... (c'est facile!). Nous trouvons: CB=8,6cm à 0,1cm près par défaut.

Remarque: ABC est-il rectangle finalement? La réponse est non (utilisez la réciproque du théorème de Pythagore ci-dessous).

La réciproque:

Si dans un triangle ABC l'égalité AB²+AC²=BC²est vérifiée

Alors le triangle ABC est rectangle en A.

Exemple:

Pour donner une solution à la remarque de l'exemple précédent: ABC est-il un triangle rectangle?

Nous avions calculé AC² (34) et BC² (74) et nous avions AB=10, d'où AB²=100. Dans un triangle rectangle le côté le plus long est toujours l'hypoténuse. Vérifions si [AB] est une hypoténuse:

Premier membre de l'égalité: AC²+ BC²=34+74=108

Deuxième membre de l'égalité: AB²=100

Comme AB² est différent de AC²+ BC² alors ABC n'est pas un triangle rectangle.

Triangle obtenu avec un point d'un cercle et l'un de ses diamètres:

Le théorème: (important)

Si un triangle est obtenu en joignant un point d'un cercle aux extrémités d'un diamètre

Alors ce triangle est rectangle en ce point.

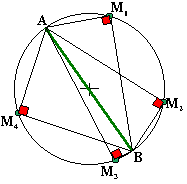
Données:

Un cercle, un point M sur le cercle, un diamètre [AB] de ce cercle.

Figure:

Sur la figure ci-contre nous avons placé plusieurs points M (indicés de 1 à 4 pour les différencier) et indiqué l'angle droit obtenu.

Remarque: cette propriété peut s'énoncer aussi:

Si le cercle circonscrit d'un triangle a pour diamètre un côté de ce triangle

Alors ce triangle est rectangle et le côté diamètre est son hypoténuse.

Droite et segment des milieux:

La droite qui passe par les milieux de deux côtés d'un triangle est parallèle au troisième côté.

La longueur du segment qui joint les milieux de deux côtés d'un triangle a pour longueur la moitié de la longueur du troisième côté.

Droite parallèle à un côté:

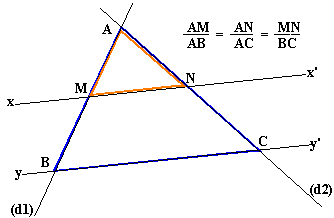
Les données sont:

le triangle ABC.
(xx') paralléle au côté (BC).
(xx') coupe [AB] en M et [AC] en N.

Ces données déterminent deux triangles: AMN et ABC dont les longueurs des côtés sont prortionnelles. Nous avons les égalités de rapports ci-contre.

La propriété peut se présenter avec les données suivantes:

Les droites (d1) et (d2) sécantes en A.
Les droites parallèles (xx') et (yy') qui coupent (d1) en M et B, et (d2) en N et C.

Si vous inversez tous les quotients, les égalités demeurent.

En pratique, vous n'utiliserez qu'une égalité à la fois, ce qui est possible de trois manières:

En utilisant les propriétés des quotients égaux vous pouvez calculer une distance en en connaissant trois autres: calcul de AM en connaissant AB, AN et AC avec la première égalité, par exemple.