|
WARMATHS |
Quotients |
- Définitions.
- Opérations sur les écritures fractionnaires:
- Addition et soustraction.
- Multiplication.
- Quotient de quotients.
- Egalités de quotients.
- Notes sur les valeurs approchées.
|
Mots clés: addition et soustraction, arrondi, coefficient de proportionnalité, dénominateur, dividende, diviseur, diviseur d'un nombre, division euclidienne, écriture fractionnaire, fraction, inverse, inverse d'un quotient, irréductible, multiple, multiplication, numérateur, par excès, par défaut, position du résultat, précision du résultat, produits en croix, quotient, quotient de quotients, quotients en géométrie, simplifier, troncature, valeur approchée. |
Définitions:
La division:
|
|
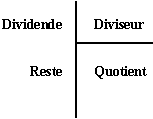
Le quotient est le résultat de la division d'un nombre (appelé Dividende) par un autre nombre (appelé Diviseur). Lorsque le quotient est exact nous pouvons écrire: Quotient = Dividende / Diviseur ou Quotient * Diviseur = Dividende Sinon nous avons l'égalité: Quotient = (Dividende - Reste) / Diviseur ou Quotient *
Diviseur + Reste = Dividende |
Remarques:
-Lorsque le quotient est exact, le reste est égal à 0. Le quotient est généralement un nombre à virgule.
-La division par 0 est impossible (mais nous pouvons diviser 0 par n'importe quel nombre non nul, dans ce cas le quotient est toujours 0).
Exemples:
1) 28 divisé par 4
quotient=28/4 ou 7 (quotient exact).
quotient*diviseur=7*4=28=dividende.
2) 45 divisé par 8
quotient=45/8 ou quotient approché à 1/10 près: 5,6 reste 0,2.
quotient=(45-0,2)/8=5,6.
quotient*diviseur+reste=5,6*8+0,2=45=dividende.
Ecritures fractionnaires:
Une fraction est un quotient dont le dividende et le diviseur sont des entiers. Ecrire un quotient sous forme fractionnaire c'est l'écrire avec un trait horizontal appelé barre de fraction. Dans cette écriture, le nombre placé au dessus de la barre est appelé numérateur, et celui placé dessous dénominateur.
Une fraction est donc un quotient mais un quotient n'est pas forcément une fraction, même si il est écrit sous forme fractionnaire. Exemple:

Pour vérifier cela effectuez les deux divisions (quotient=1,5).
Division euclidienne:
La division euclidienne est une division dont le quotient est un nombre entier (dans le calcul du quotient nous nous arrêtons à la virgule). Sur certaines calculatrices il est possible d'effectuer une division euclidienne à l'aide d'une touche, le résultat est donné sous forme de deux nombres, le quotient et le reste. Par exemple:
![]()
Opérations sur les écritures fractionnaires:
Ecritures fractionnaires équivalentes:
On ne change pas la valeur d'un quotient si on multiplie, ou divise, le numérateur et le dénominateur de son écriture fractionnaire, par le même nombre (entier ou pas).
Nous utiliserons la multiplication du numérateur et du dénominateur pour additionner ou soustraire, la division par un entier pour simplifier l'écriture fractionnaire.
L'écriture fractionnaire est irréductible lorsque numérateur et dénominateur n'ont plus de diviseur commun.
Rappel: un nombre n est diviseur d'un nombre N lorsqu'on peut trouver un nombre k tel que:
N=k.n
par exemple, 5 est un diviseur de 100 (k est égal à 100:5=20) car 100=20*5.
Exemples:
- Le quotient 7/5 peut s'écrire aussi 14/10, 21/15, 70/50 (multiplication des numérateurs et dénominateurs successivement par 2, 3, 10). Ce qui se vérifie aisément avec une calculatrice.
- 27 et 18 ont 1, 3 et 9 comme diviseurs communs.
- pour simplifier 27/18 il faut diviser 27 et 18 par l'un de leur diviseur commun (le mieux est de choisir le plus grand: l'écriture obtenue sera alors irréductible). Nous obtenons: 3/2.
Addition et soustraction:
Pour additionner ou soustraire des quotients sous forme d'écritures fractionnaires il est nécessaire que les dénominateurs soient égaux. Si les quotients à ajouter (ou soustraire) ont:
a) des dénominateurs égaux:
Le résultat a le même dénominateur et a pour numérateur la somme (différence) des numérateurs.
b)des dénominateurs différents:
Vous remplacerez les dénominateur par un dénominateur commun qui est un multiple commun des dénominateurs donnés. Après avoir recalculé les numérateurs (voir l'exemple ci-dessous) vous opérez comme au a) .
Rappel: on obtient un multiple d'un nombre en le multipliant par un nombre entier (Ex: les multiples de 12 sont obtenus en multipliant 12 par 0, puis par 1, par 2, 3, 4, 5, ...).
Exemple: somme de 9/25, 12/75 et 7/50 dont les dénominateurs sont 25, 75 et 50.
Le multiple commun à ces trois dénominateurs est un nombre que l'on obtient en multipliant 25, 75 et 50 par un nombre entier (différent pour chacun d'eux bien sûr!). Vous pouvez le trouver facilement en choisissant le plus petit (25), en le multipliant par un nombre entier de plus en plus grand et en vérifiant chaque fois si les deux autres (75 et 50) l'acceptent aussi comme multiple:
2 fois 25 égale 50, c'est bon pour le troisième nombre mais pas le second,
3 fois 25 égale 75, c'est bon pour le deuxième mais pas pour le troisième.
...., 6 fois 25 égale 150, ce qui convient pour 75 (2 fois 75 égale 150) et 50 (3 fois 50 égale 150). Notez bien les entiers (6, 2 et 3) qui vous ont permis de calculer 150 chaque fois: ils vont servir pour calculer les nouveaux numérateurs (comme ci-dessous vous pouvez les noter au fur et à mesure que vous les trouvez).
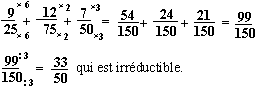
Remarques:
- il est parfois très intéressant de chercher à simplifier les écritures fractionnaires avant d'effectuer tout calcul. Dans l'exemple précédent le deuxième quotient peut se simplifier en divisant numérateur et dénominateur par 3 (on obtient 4/25). Le dénominateur commun est ramené à 50 (puisque les dénominateurs sont maintenant 25, 25 et 50).
- la méthode qui consiste à multiplier entre eux tous les dénominateurs, pour trouver le dénominateur commun, conduit parfois à des nombres très grands. Si vous devez ensuite simplifier votre résultat, le travail risque de ne pas en être facilité. Avec l'exemple précédent:
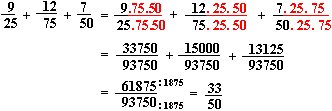
ce qui n'est pas très confortable, convenez en!
Multiplication:
Pour effectuer le produit de quotients sous forme d'écritures fractionnaires, il suffit d'effectuer les produits des numérateurs, puis le produit des dénominateurs (ne mettez surtout pas au même dénominateur, vous feriez des calculs inutiles qui vous compliqueraient la tâche). Il ne reste plus qu'à simplifier le résultat si possible.
Exemple: ![]()
Remarque:
Dans une multiplication nous pouvons simplifier sur deux quotients en même temps comme ci-dessus. Il faut diviser autant de numérateurs que de dénominateurs, pas forcément du même quotient (ici nous n'avons pu simplifier qu'un numérateur et un dénominateur de quotients différents).
Quotient de quotients:
a)Inverse d'un nombre non nul:
Si le produit a.b est égal à 1 Alors a est l'inverse de b (et b est l'inverse de a)
Par exemple: comme 2 fois 0,5 égale 1 alors 2 est l'inverse de 0,5 (et 0,5 est l'inverse de 2).
Dans l'égalité a.b=1 nous pouvons considérer a comme un quotient, b comme un diviseur et 1 comme le dividende ( revoir Division dans ce document). Nous pouvons donc écrire que a=1/b. Donc:
Si a est l'inverse de b Alors a=1/b
Par exemple: l'inverse de 2 est 1/2 (c'est à dire 0,5).
b)Inverse d'un quotient:
L'inverse de a/b est b/a. En effet:
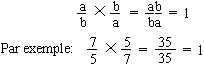
c) Quotient de deux quotients:
c'est à dire que l'un des quotients est le dividende (ou le numérateur) l'autre le diviseur (ou le dénominateur). Le quotient de a/b (dividende) par c/d (diviseur) est le produit de a/b par l'inverse de c/d (c'est à dire par d/c).
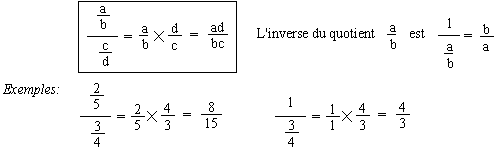
Remarque: attention à la longueur des barres
Egalités de quotients:
Suites proportionnelles et quotients:
|
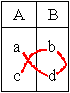
Soient A=(a,c) et B=(b,d) deux « suites proportionnelles. » On sait que le coefficient de proportionnalité de A vers B est calculé en divisant un nombre de la suite B par le nombre de même rang de la suite A. Nous avons donc: b/a = d/c. D'autre part les « produits en croix » nous permettent d'écrire: a . d = b . c Nous retiendrons alors que:
|
|
Utilisation dans les calculs:
La propriété précédente est très utilisée lorsqu'il y a des quotients dans des égalités et notamment dans des « équations » obtenues en calculant une distance avec le « cosinus d'un angle » ou avec le « théorème des deux sécantes coupées par deux droites parallèles ». Nous allons donner un exemple utilisant ce dernier théorème, les autres situations ayant déjà été étudiées par ailleurs.
Exemple: Les droites parallèles d et d' coupent les droites sécantes (Ax) et (Ay) comme il est indiqué sur la figure ci-dessous. Les dimensions sont en centimètres (la figure ne respecte pas ces dimensions).
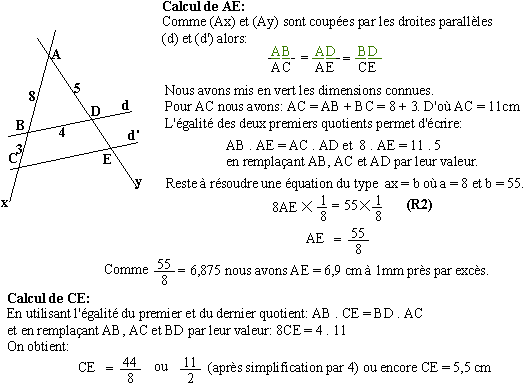
Remarque: la notation (R2), dans le calcul de AE, fait référence à la méthode utilisée pour résoudre ce type d'équation.
Notes sur les valeurs approchées:
Il est parfois impossible de donner un quotient exact. Par exemple: 1/3 ne peut pas s'écrire exactement autrement que 1/3 ! Dans ce cas nous pouvons donner une valeur approchée de ce quotient. Il faut alors indiquer qu'elle est la précision du calcul et comment se situe le résultat donné par rapport au résultat brut de l'opération .
Précision: concerne le nombre de chiffre après la virgule. Il peut y avoir 1, 2, 3, ... chiffres après la virgule, ce qui signifie que la précision est à 1/10, 1/100, 1/1000, ... de l'unité près. Par exemple: 2,54m à 1/100 de mètre près.
Position du résultat: vous trouvez par exemple sur votre calculatrice le résultat 2,54895578129 qui n'est vraisemblablement pas exact! Vous n'avez besoin que de deux chiffres après la virgule, c'est à dire une précision de 1/100. Vous pouvez:
- effectuer une troncature: c'est à dire ne garder que les deux chiffres après la virgule sans vous préoccuper de ceux qui suivent. Dans ce cas le résultat que vous écrivez, c'est à dire 2,54 est à 1/100 de l'unité près par défaut. Ce qui est logique puisqu'il manque 0,00895578129 (les chiffres écartés) dans votre résultat, il est donc plus faible que le résultat brut trouvé. Attention, si le résultat est négatif, par exemple vous lisez -2,54895578129, le fait de ne pas tenir compte des chiffres après le 4 vous permet d'écrire -2,54 qui est un nombre plus grand que ce que vous lisez sur votre calculatrice! Il s'agit alors d'un résultat par excès. Rappel: si deux nombres sont négatifs alors le plus grand est celui qui a la plus petite valeur absolue.
- effectuer un arrondi: c'est à dire tenir compte des chiffres qui suivent avant de décider de les écarter de votre résultat. La méthode est relativement simple:
si le premier chiffre de la suite de chiffres que vous désirez enlever ( le 8 dans notre exemple) est inférieur à 5 (ce qui n'est pas le cas dans l'exemple) vous tronquez (vous enlevez tous ces chiffres sans plus de cérémonie). Vous écrivez alors un arrondi par défaut (par excès si le nombre est négatif).
si ce chiffre est supérieur ou égal à 5 (ce qui est le cas cette fois) alors vous augmentez de 1 le dernier chiffre que vous gardez, et vous tronquez comme ci-dessus. Vous écrivez cette fois un arrondi par excès (par défaut si le nombre est négatif). Dans notre exemple cela donne: 2,55 à 1/100 près par excès.
Exemples: écrire les deux valeurs approchées de 0,015447 et choisir la meilleure:
à 1/100000 près: 0,01544 par défaut et 0,01545 par excès. Ecrire la valeur par excès (qui est un arrondi), elle est plus près de la vraie valeur (0,015450 est plus près de 0,015447 que 0,015440).
à 1/1000 près: 0,015 par défaut et 0,016 par excès. Ecrire la valeur par défaut (le quatrième chiffre est un 4, il ne faut donc pas arrondir par excès mais par défaut).
à 1/10 près: 0,0 par défaut et 0,1 par excès. La valeur à écrire est 0,0 (logiquement 0,000 est plus proche de 0,015 que 0,100)