|
WARMATHS : Collège. |
|
|
|
INFO +++ @ |
|
|
|
INFO +++ @ |
|
|
|
INFO +++ @ |
|
|
|
Construction du point symétrique d'un point donné. |
INFO +++ @ |
|
|
Figures possédant au moins un axe de symétrie. |
INFO +++ @ |
|
|
Symétriques de quelques figures simples. |
INFO +++ @ |
|
|
Propriétés conservées par la symétrie axiale. |
INFO +++ @ |
|
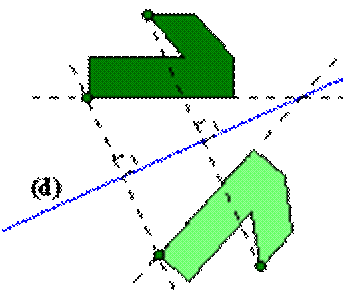
Sur le dessin ci-contre, tout ce qui est en haut est représenté en bas mais "à l'envers". La transformation qui permet de faire correspondre, sur le dessin, un point du haut avec un point du bas est appelée symétrie orthogonale ou axiale (orthogonale pour une raison que nous allons voir dans la suite). |
|
Les points communs au haut et au bas sont sur une droite appelée axe de symétrie (en bleu clair sur le dessin). C'est pour cette raison que la symétrie orthogonale est aussi appelée symétrie axiale.
Les points qui se correspondent, dans une symétrie orthogonale, sont symétriques l'un de l'autre par rapport à l'axe.
Remarque: le dessin ci-dessus ne fait qu'illustrer une symétrie orthogonale particulière. En Géométrie, les termes: "haut", "bas", "à l'envers" n'ont pas de signification.
Prenez une feuille de papier. Pliez la en deux. Avec la pointe d'un compas, faites un trou dans les deux épaisseurs de papier. Dépliez et tracez la droite (xy) représentée par le pli, ainsi que le segment joignant les deux trous A et B. Observez la figure obtenue avec une équerre et un double décimètre (ou mieux: un compas). Qu'en conclure? Voir le paragraphe suivant.
3°) Propriété caractéristique:
L'axe de symétrie (xy) est la médiatrice du segment [AB]. Donc:
Si deux points sont symétriques par
rapport à une droite
Alors cette droite est médiatrice du
segment d'extrémités ces deux points.
Construction du
point symétrique d'un point donné:
Données: l'axe de symétrie (xy), le point A.
Construire le
point B, symétrique de A par rapport à (xy).
|
Nous devons obtenir la figure
ci-contre. Pour cela il faut que l'axe (xy) soit perpendiculaire au segment
[AB] en son milieu (puisque (xy) doit être la médiatrice de [AB]): Première façon:
|
|
|
Deuxième façon: Le
point A étant connu, l'axe (xy) doit être la médiatrice de [AB]. Pour
construire le point B nous allons utiliser la propriété suivante: tout point d'une médiatrice d'un
segment est équidistant des extrémités de ce segment. Nous choisissons deux points quelconques
« P » et « Q » de (xy) et nous allons déterminer un point
B tel que PA= PB et QA= Q B. Ainsi nous sommes certains que (PQ),
c'est à dire (xy), est la médiatrice de [AB]. Construction:
|
|
Remarques:
·
Si B
est le symétrique de A par rapport à (xy) alors A est symétrique de B par
rapport à (xy). Nous dirons plus simplement que A et B sont symétriques par
rapport à (xy).
·
Le
point B, symétrique de A, est aussi appelé image de A par la symétrie d'axe (xy).
·
Si le point A est sur l'axe (xy) alors son symétrique est lui
même.
·
Le fait que le segment joignant un point et son symétrique, soit
orthogonal à l'axe, justifie l'appellation de symétrie orthogonale.
Figures
possédant au moins un axe de symétrie:
Une figure possède un axe de
symétrie lorsqu'en la pliant selon cet axe, les deux parties de la figure se
superposent. Exemples de figures usuelles:

Le cercle possède une infinités
d'axes de symétrie: tous ses diamètres.
Un angle quelconque a toujours un
axe de symétrie: sa bissectrice.
Le triangle isocèle possède un axe
de symétrie: sa bissectrice
principale.
Le triangle équilatéral possède
trois axes de symétrie: ses 3 bissectrices .
Le losange en possède deux: ses 2 diagonales.
Le rectangle en possède deux: ses
2 médianes.
Le carré en possède quatre: ses 2
diagonales (puisque c'est aussi un losange) et ses 2 médianes (puisque c'est
aussi un rectangle).
Symétriques de quelques
figures simples:
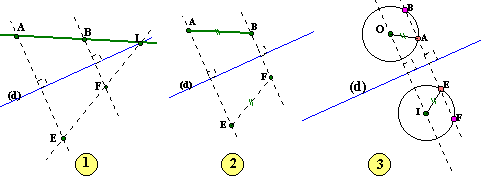
Sur les figures ci-dessous, l'axe
de symétrie est noté (d) et coloré en bleu. La figure à transformer est
coloriée en vert. Les points remarquables sont représentés par des petits
disques de couleur.
Je vous conseille de tracer ces
figures (c'est la meilleure manière de comprendre les propriétés des symétries
axiales). Utilisez un papier non quadrillé et apprenez d'abord à construire le symétrique d'un point par rapport à une droite
(cette construction est essentielle).
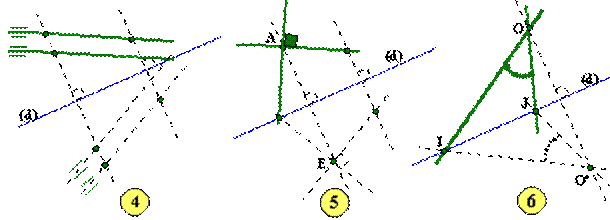
Propriétés conservées par
la symétrie axiale:
Le paragraphe précédent illustre
les propriétés suivantes:
Les symétries orthogonales conservent:
Les distances
(fig 2 et fig 3).
Le parallélisme et l'orthogonalité (fig
4 et 5).
Les mesures des angles (fig 6) et les
alignements.
Les aires: le calcul sur les aires utilise des
longueurs et des propriétés (angles notamment) qui sont conservées.