WARMATHS

Résumé : collège .

Les Quadrilatères

Définitions.
Droites particulières.
Quadrilatères particuliers.

Définitions:

Un quadrilatère est un polynôme qui possède quatre côtés, quatre angles, quatre sommets. Les deux figures ci-dessous représentent le même quadrilatère.

Un côté est considéré soit comme un segment ( [AB],[BC],[CD],[DA]) soit comme une droite ( (AB),(BC),(CD),(DA) ). C'est le contexte qui nous informe: c'est le segment qui est considéré si il est question de longueur ou de milieu. Dans les autres cas c'est aussi bien la droite que le segment ( lorsqu'il est question de parallèles, de perpendiculaires, de diagonales, de médianes, de hauteurs; voir la signification de ces mots plus loin dans ce document).

Deux côtés, considérés comme segment, sont consécutifs lorsqu'ils ont une extrémité commune ( [AD] et [AB] par exemple). Ils sont opposés dans le cas contraire ( [AD] et [BC] par exemple)

Les sommets A et B sont dits consécutifs (de même pour A et D, D et C, B et C,...). Les sommets A et C sont dits opposés (ainsi que B et D).

En général les quatre angles sont tous différents. Mais leur somme est égale à 360° (tracez [BD]: la somme des angles des triangles ABD et CBD est chacune 180°...).

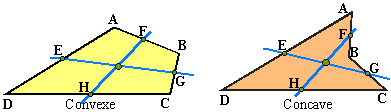
Un quadrilatère est convexe si tous ses angles sont des angles saillants. Si le quadrilatère possède un angle rentrant alors il est concave. Le quadrilatère de la figure ci-dessus est convexe, celui de la figure ci- dessous est concave (l'angle en B est rentrant).

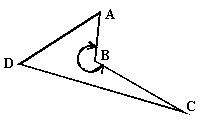
Droites particulières:

Diagonales: les diagonales sont les droites qui passent par deux sommets opposés. Les diagonales d'un quadrilatère convexe se coupent à l'intérieur, celles d'un quadrilatère concave se coupent à l'extérieur du quadrilatère considéré (c'est un bon moyen de les distinguer). Sur les figures ci-dessous, l'intérieur du quadrilatère est colorié.

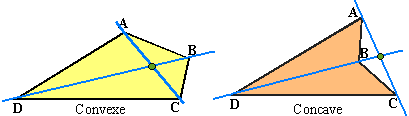
Médianes: les médianes d'un quadrilatères sont les droites qui passent par les milieux de deux côtés opposés. Sur les figures ci-dessous les milieux des côtés sont les points E, F, G et H. Ces médianes se coupent toujours en leur milieu (c'est à démontrer...en utilisant plusieurs fois le "théorème de la droite des milieux" après avoir tracé les diagonales)

Hauteurs: les hauteurs d'un quadrilatère sont les droites qui passent par un sommet perpendiculairement à un côté. Il existe deux hauteurs par sommet. Par exemple pour le sommet B: les hauteurs sont (BH) et (BI), les longueurs des segments [BH] et [BI] expriment la distance (la hauteur est ici considérée comme un nombre) du sommet B aux côtés (AD) et (DC).

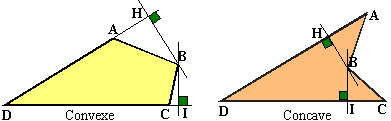
Quadrilatères particuliers:

Les parallélogrammes: ce sont des quadrilatères qui ont leurs côtés parallèles deux à deux.

Les trapèzes: ce sont des quadrilatères qui ont deux côtés parallèles appelés bases. Dans ce sens, les parallélogrammes sont des trapèzes particuliers. Nous distinguerons:

· Le trapèze quelconque: rien de spécial à part les deux côtés parallèles.

· Le trapèze rectangle: il possède en plus deux côtés consécutifs perpendiculaires.

Dans le trapèze ABCD dont les côtés (AB) et (CD) sont parallèles, les côtés (AB) et (AD) sont perpendiculaires. Ce qui entraîne: comme (AB) et (CD) sont parallèles et (AD) est perpendiculaire à (AB) alors (AD) est perpendiculaire à (CD) (propriété des droites parallèles). Il y a donc deux angles droits dans un trapèze rectangle.

· Le trapèze isocèle: dans ce type de trapèze, les deux côtés non parallèles ont même longueur. Un trapèze isocèle possède un axe de symétrie: la médiatrice commune aux bases. Les angles opposés sont supplémentaires et les angles dont un côté commun est une base, ont même mesure (les angles en D et en C par exemple). Le trapèze isocèle possède un cercle circonscrit (passant par les quatre sommets) dont le centre se trouve sur l'axe de symétrie et sur l'une des médiatrices d'un des côtés de même longueur.

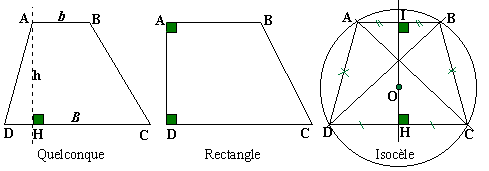
trapèzes

Remarque: pour calculer l'aire d'un trapèze nous utilisons la formule:

ou B et b sont les longueurs des grandes et petites bases, h est la distance entre les deux côtés parallèles, communément appelée "hauteur du trapèze". Dans le trapèze rectangle h est égal à la longueur du côté perpendiculaire aux deux côtés parallèles. Dans un trapèze isocèle h est égal à, par exemple, IH (voir figure ci-dessus). Il est possible de choisir d'autres hauteurs ( distance de A au côté (BC) par exemple) mais dans ces cas, la formule ne s'applique plus et les calculs sont plus complexes (il faut plusieurs hauteurs).