|
WARMATHS |
|
Droites parallèles
·
Définition.
·
Propriétés.
·
Tracé d'une droite parallèle à une droite
donnée.
·
Quadrilatères et côtés parallèles
·
Parallèles coupées par une sécante.
· Droites parallèles coupant deux droites sécantes.
Définitions:
Deux droites parallèles sont deux droites
qui n'ont aucun point commun ou qui sont confondues.
Si deux droites ont un point commun alors
elles sont sécantes en ce point.
Propriétés:
1. Axiome
d'Euclide: il n'existe qu'une seule droite parallèle à une droite donnée et
passant par un point donné.
Remarque: Un axiome est une
propriété non démonstrée, admise par tous les
mathématiciens.
2. Si deux
droites sont parallèles et qu'une troisième droite est sécante à l'une
Alors
cette troisième droite est sécante à l'autre.
3. Si deux droites sont parallèles et
qu'une troisième droite est perpendiculaire à l'une
Alors
cette troisième droite est perpendiculaire à l'autre.
|
4. Si deux droites
sont parallèles à une même troisième Alors
ces deux droites sont parallèles entre elles. |
|
Tracé d'une droite parallèle à une droite donnée:
|
1.
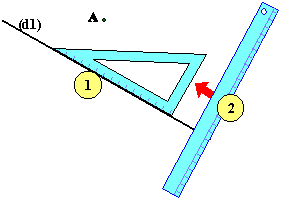
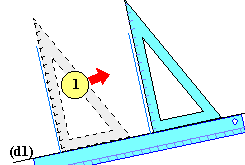
Passant par un point donné: Soit (d1) la droite donnée
et tracer (d2) parallèle à (d1) passant par A. Se fait en trois points: 1.
alignez un côté (n'importe lequel) de
l'équerre avec la droite donnée (d1). 2.
Placez une règle sur un autre côté de
l'équerre.
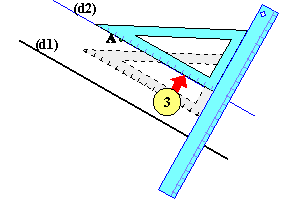
3.
Tenir fermement la règle (ne pas la
bouger!) et glissez l'équerre sur la règle jusqu'à ce que le côté qui était
aligné avec (d1) passe sur le point A. Tracez la droite (d2) en suivant ce
côté.
Il ne reste plus qu'à la
prolonger convenablement. |
|
|
2. A une distance
donnée: Soit (d1) la droite donnée. Tracer (d2)
parallèle à (d1) à une distance d (5cm par exemple). Voici une méthode (parmi
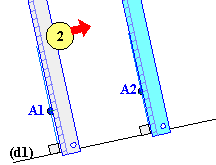
d'autre) rapide mais peu précise: 1.
Placez la règle alignée avec la droite (d1). Avec
l'équerre appuyée sur la règle (celle ci ne bouge pas) tracez deux segments
perpendiculaires à (d1). Remarque: ces deux segments sont parallèles (à
démontrer en utilisant une propriété des droites perpendiculaires et non la
propriété 3 du paragraphe "propriétés" ci-dessus). 2.
Mesurez sur chacun de ces segments, à partir de
leur intersection avec (d1), la distance donnée (5cm par exemple). Vous
obtenez deux points A1 et A2. La droite passant par ces deux points
est la droite (d2) demandée. Remarque: la démonstration se fait en remarquant
que nous avons tracé un parallélogramme (et même un rectangle). |
|
Quadrilatères et côtés parallèles:
Deux côtés parallèles: les trapèzes.
Côtés opposés parallèles deux à deux: les parallélogrammes.
Parallèles
coupées par une sécante:
Un peu de vocabulaire:
Deux angles de part et d'autre d'une
droite sont dits alternés comme les feuilles sur les tiges de certaines
plantes:

Ces angles ne sont égaux que dans des
situations particulières.
Une bande à bords parallèles est la
partie du plan situé entre deux droites parallèles. Si les deux bords sont
sécants alors la bande est un angle et les propriétés rappelées ci-dessous ne
sont plus vérifiées.
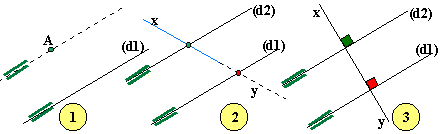
Définitions:
« angles
alternes internes »:
ils se trouvent à l'intérieur de la bande de part et d'autre de la sécante, les
sommets sont différents.
« angles alternes externes »: ils se trouvent à l'extérieur de la bande, de part et d'autre
de la sécante, les sommets sont différents.
« angles
correspondants »: ils se trouvent du même côté de la sécante, l'un à l'intérieur de
la bande, l'autre à l'extérieur; les sommets sont différents.
Cas particulier des bandes à bords
parallèles:
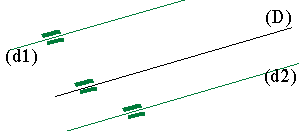
Les droites parallèles (d1) et (d2)
déterminent une bande à bords parallèles. Sur les figures ci-dessous,
l'intérieur de cette bande est "grisée". Les angles à l'intérieur de
la bande sont appelés internes, ceux à l'extérieur de la bande sont appelés...
externes.
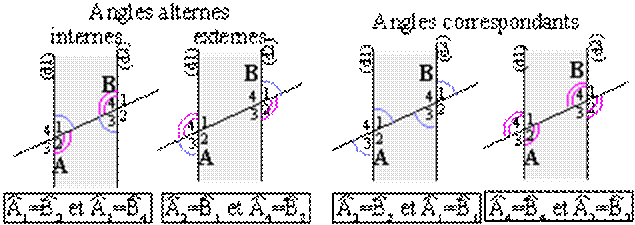
Dans ce cas particulier, les angles
alternes internes sont égaux (deux par deux) ainsi que les angles alternes
externes (deux par deux) et les angles correspondants (deux par deux).
Droites
parallèles coupant deux droites sécantes:
|
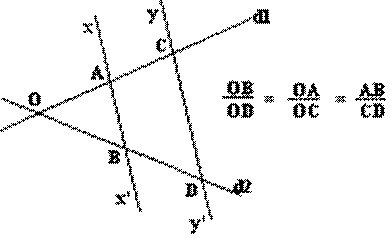
Les
droites (d1) et (d2) sont sécantes en O. Les
deux droites parallèles (xx') et (yy') coupent ces
deux sécantes en A et B pour (xx') et en C et D pour (yy'). Cette
configuration détermine deux triangles: OAB et OCD dont les côtés sont liés
par les égalités ci-contre. Pour l'utilisation de ces formules il vous faut
savoir calculer avec des quotients égaux. Voir
aussi ce qui est dit sur la droite parallèle à un côté d'un triangle. |
|