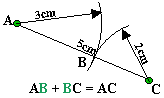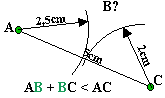|
WARMATHS. Résumé collège |
Distance
|
- Définitions.
- Calcul d'une distance.
- Inégalité triangulaire.
- Distance d'un point à une droite.
- Point équidistant d'autres points.
- Point équidistant de plusieurs droites.
- Distance entre deux droites parallèles.
Définitions:
Une distance est toujours un nombre.
La distance du point A au point B est notée AB . Ne pas confondre avec [AB] qui est un segment, représenté par un morceau de droite; les crochets, tels qu'ils sont présentés ici , signifient que A et B appartiennent au segment.
Le mot "distance" est utilisé dans les situations suivantes:
· Distance entre deux points (longueur d'un segment, du rayon d'un cercle,..)
· Distance d'un point à une droite.
· Distance entre deux droites parallèles.
Calcul d'une distance:
Sur une figure on peut calculer une distance à l'aide de théorèmes comme:
· Théorème de Pythagore.
· Droites sécantes coupées par deux droites parallèles.
· Cosinus d'un angle.
· Droite des milieux.
· Milieu d'un segment.
· Symétrie orthogonale et symétrie centrale
Inégalité triangulaire:
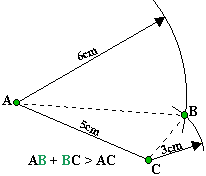
Soient trois points A, B et C. Ils constituent un triangle de côtés [AB], [AC] et [BC]. Si nous connaissons la longueur de ces trois côtés, nous pouvons construire le triangle ABC. Sur les figures suivantes nous supposons que:
Cas 1: AB = 6cm AC = 5cm et BC = 3cm
Cas 2: AB = 3cm AC = 5cm et BC = 2cm
Cas 3: AB = 2,5cm AC = 5cm et BC = 2cm
|
|
|
|
Mais une condition doit être remplie: il faut que la somme des mesures de deux côtés (ici: AB+BC) soit supérieure (1ère figure) ou égale (2ème figure) à la mesure du troisième côté. Si cette condition n'est pas vérifiée (cas de la 3ème figure où 2,5 + 2 = 4,5 est inférieur à 5) il n'est pas possible de construire le 3ème sommet B. Cette condition est appelée "inégalité triangulaire" et s'énonce:
AB + BC >= AC
Dans le cas de l'égalité, le point B se trouve sur le segment [AC] (Attention: pas forcément au milieu).
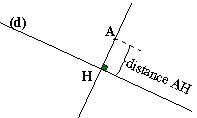
Distance d'un point à une droite:
La distance du point A à la droite (d) est la plus courte distance entre le point A et un point particulier de (d). Ce point particulier est l'intersection de la droite perpendiculaire à (d) et passant par A.
Voir "Droites perpendiculaires" pour son tracé.
|
H est appelé pied de la perpendiculaire à (d) passant par A. |
|
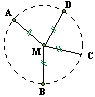
Point équidistant d'autres points:
|
Un point M équidistant des points A, B, C, ... est le centre du cercle passant par ces points. Ce cercle est le cercle circonscrit au polygone défini par ces points. |
|
|
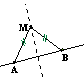
Un point M équidistant de deux point A et B est sur la médiatrice du segment [AB].
|
|
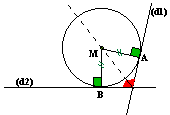
Point équidistant de plusieurs droites:
|
Un point M équidistant de deux droites (d1) et (d2) sécantes est sur la bissectrice de l'angle dont les côtés sont (d1) et (d2). Remarque: si (d1) et (d2) sont parallèles alors elles ne se coupent pas et le sommet de l'angle n'existe pas. |
|
|
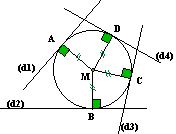
Un point M équidistant des droites (d1), (d2), (d3),... est le centre du cercle tangent à ces droites. Ce cercle est inscrit dans le polygone formé par les droites. |
|
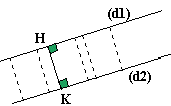
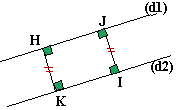
Distance entre deux droites parallèles:
|
Les droites (d1) et (d2) sont parallèles. La distance de (d1) à (d2) est la distance d'un point quelconque de l'une à l'autre droite. Si on choisit H sur (d1) alors la distance de (d1) à (d2) est la mesure du segment [HK] où K est tel que [HK] est perpendiculaire à (d2). |
|
|
Cette
distance est toujours la même, quelque soit le point choisi sur (d1) ou (d2).
Ce qui se remarque bien sur un rectangle. |
|