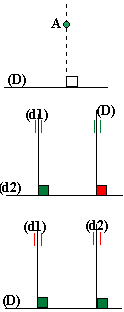warmaths

Droites perpendiculaires

Avec l'équerre.
Sans l'équerre.

Définitions:

Deux droites perpendiculaires constituent les côtés d'un angle droit.

Deux droites perpendiculaires sont toujours sécantes (se coupent en un point). Mais deux droites sécantes ne sont pas toujours perpendiculaires.

Vocabulaire:

Si A n'appartient pas à (d) alors on peut dire: abaisser de A une droite perpendiculaire à (d). Même si, sur la figure que l'on étudie, le point A est "dessous" la droite (d).

Si A appartient à (d) alors on peut dire: élever de A une droite perpendiculaire à (d). Même si, sur la figure que l'on étudie, la droite perpendiculaire se prolonge "dessous" la droite (d).

Propriétés:

1. Par un point donné ne passe qu'une droite perpendiculaire à une droite donnée.

2. Si deux droites sont perpendiculaires ET une troisième droite est parallèle à l'une

Alors cette troisième droite est perpendiculaire à l'autre.

3. Si deux droites sont perpendiculaires à une même troisième

Alors ces deux droites sont parallèles.

Remarques:

Les propriétés 2 et 3 ci-dessus semblent représentées par les mêmes figures... Attention! Bien lire les énoncés de ces propriétés. Sur les figures ce qui est représenté en vert (rouge) est ce qui est écrit en vert (rouge).

Pour la propriété 2 ce qui est connu (vert) est: (d1) et (d2) perpendiculaires (un petit carré vert) ainsi que (D) parallèle à (d1) (symboles du parallélisme en vert). Ce qui peut être démontré est (D) perpendiculaire à (d2) (un petit carré rouge).

Pour la propriété 3: ce qui est connu est (d1) ET (d2) perpendiculaires à (D) (deux petits carrés verts). Ce qui peut être démontré est (d1) et (d2) parallèles (symbole du parallélisme en rouge).

Construction d'une droite perpendiculaire à une droite donnée et passant par un point donné:

Pour tracer cette droite perpendiculaire on peut:

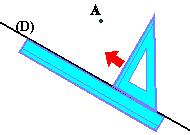
1° Utiliser une équerre: c'est la méthode la plus rapide mais la moins précise. Pour améliorer la précision sans perte de temps, on doit utiliser l'équerre avec une règle qui est posée en suivant la droite (d), un côté de l'angle droit de l'équerre est posée sur la règle et l'équerre est glissée sur la règle jusqu'à ce que l'autre côté de l'angle droit passe par le point A.

2° Utiliser le compas et la règle: méthode très précise (lorsque les crayons sont bien affûtés...).

Lorsque le point A n'est pas sur la droite (d): Elle se déroule en six temps illustrés ci-dessous:

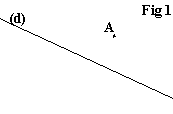
La droite (d) et le point A sont placés.
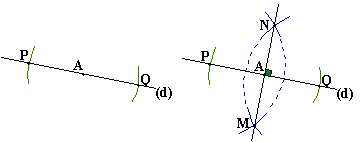
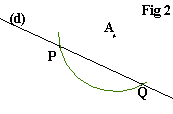
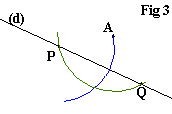
Pointe sèche du compas en A avec un écartement quelconque (il faut cependant que l'arc de cercle (en vert sur la figure) coupe la droite (d) en deux points P et Q (inutile de les nommer sur votre figure).
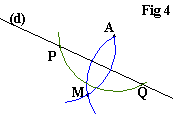
Pointe sèche en P, tracer un arc de cercle (en bleu sur la figure) en gardant le même écartement que pour la figure 2.
Même chose que ci-dessus mais avec la pointe sèche en Q et toujours le même écartement.
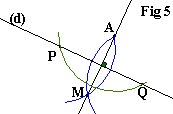
Ces deux arcs (attention à ne pas confondre avec le premier arc tracé, celui qui permet de déterminer P et Q, en vert sur la figure) se coupent en M (inutile de le nommer sur votre figure). Avec la règle tracer la droite (d) qui passe par A et M (en fait nous venons de tracer la médiatrice du segment [PQ]...)
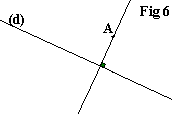
Gommer les traits de construction. Dès que vous aurez bien compris la méthode et afin de réduire l'encombrement de votre figure, je vous conseille de limiter le tracé des arcs au voisinage des points que l'on veut obtenir.

Lorsque le point A est sur la droite (d): les points Q et P sont déterminés de la même façon que ci-dessus. Mais il faut, pour déterminer le point M, un écartement plus grand (sinon les deux arcs ne se coupent pas). Il suffit ensuite de joindre A et M et de prolonger la droite. Un autre point peut être déterminé, de l'autre côté de (d), illustré sur la figure ci-dessous par le point N.